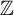1 Introduction
An exponential equation over a group G is an equation of the form
where
![]() $a_1,g_1,\dots , a_n,g_n$
are elements from G and
$a_1,g_1,\dots , a_n,g_n$
are elements from G and
![]() $x_1,\dots ,x_n$
are variables which take values in
$x_1,\dots ,x_n$
are variables which take values in
![]() $\mathbb {Z}$
. We always assume that G is given by a recursive presentation
$\mathbb {Z}$
. We always assume that G is given by a recursive presentation
![]() $\langle X\,|\, R\rangle $
. In this paper, we study the exponential equations problem (briefly
$\langle X\,|\, R\rangle $
. In this paper, we study the exponential equations problem (briefly
![]() ${\mathrm {EE}}$
-problem), which is the following decision problem:
${\mathrm {EE}}$
-problem), which is the following decision problem:
Given an exponential equation over G, decide if it has a solution, which is a tuple of integers.
The study of exponential equations in groups was initiated by Myasnikov, Nikolaev, and Ushakov in [Reference Myasnikov, Nikolaev and Ushakov17], where they showed that the
![]() ${\mathrm {EE}}$
-problem is algorithmically decidable in any hyperbolic group G. According to [Reference Lohrey11], it is in LogCFL, a subclass of P. The study of problems related to the
${\mathrm {EE}}$
-problem is algorithmically decidable in any hyperbolic group G. According to [Reference Lohrey11], it is in LogCFL, a subclass of P. The study of problems related to the
![]() ${\mathrm {EE}}$
-problem and its complexity in various families of groups has become a very active area of investigations that uses methods of geometric and combinatorial group theory, automata, complexity theory, recursive functions, and logic (see [Reference Dudkin and Treyer4–Reference Ganardi, König, Lohrey and Zetzsche7, Reference König, Lohrey and Zetzsche9–Reference Lohrey and Zetzsche13, Reference Mishchenko and Treier16]).
${\mathrm {EE}}$
-problem and its complexity in various families of groups has become a very active area of investigations that uses methods of geometric and combinatorial group theory, automata, complexity theory, recursive functions, and logic (see [Reference Dudkin and Treyer4–Reference Ganardi, König, Lohrey and Zetzsche7, Reference König, Lohrey and Zetzsche9–Reference Lohrey and Zetzsche13, Reference Mishchenko and Treier16]).
We mention results of Lohrey and Zetzsche on right-angled Artin groups and on virtually special groups [Reference Lohrey and Zetzsche12], of Mishchenko and Treier on nilpotent groups [Reference Mishchenko and Treier16], and of Dudkin, Treyer, Lohrey, and Zetzsche on Baumslag–Solitar groups BS
![]() $(n,m)$
(see [Reference Dudkin and Treyer4, Reference Lohrey and Zetzsche13]). König, Lohrey, and Zetzsche studied in [Reference König, Lohrey and Zetzsche9] the
$(n,m)$
(see [Reference Dudkin and Treyer4, Reference Lohrey and Zetzsche13]). König, Lohrey, and Zetzsche studied in [Reference König, Lohrey and Zetzsche9] the
![]() ${\mathrm {EE}}$
-problem for the Heisenberg group
${\mathrm {EE}}$
-problem for the Heisenberg group
![]() $\mathrm {H}_3(\mathbb {Z})$
and its direct products. Continuing the line of [Reference Myasnikov, Nikolaev and Ushakov17], Lohrey described solutions of exponential equations in hyperbolic groups (see [Reference Lohrey11]). Bier and Bogopolski showed in [Reference Bier and Bogopolski1] that if G is a relatively hyperbolic group with respect to a finite collection of subgroups
$\mathrm {H}_3(\mathbb {Z})$
and its direct products. Continuing the line of [Reference Myasnikov, Nikolaev and Ushakov17], Lohrey described solutions of exponential equations in hyperbolic groups (see [Reference Lohrey11]). Bier and Bogopolski showed in [Reference Bier and Bogopolski1] that if G is a relatively hyperbolic group with respect to a finite collection of subgroups
![]() $\{ H_1,\dots ,H_n\}$
, then the
$\{ H_1,\dots ,H_n\}$
, then the
![]() ${\mathrm {EE}}$
-problem for G reduces to the
${\mathrm {EE}}$
-problem for G reduces to the
![]() ${\mathrm {EE}}$
-problems for
${\mathrm {EE}}$
-problems for
![]() $H_i$
’s, provided some natural assumptions are satisfied.
$H_i$
’s, provided some natural assumptions are satisfied.
In this paper, we study the EE-problem and its complexity in general, i.e., not focusing on a specific class of groups. For the forthcoming discussion, it is convenient to introduce the following definition.
Definition 1.1 Let G be a group, and let n be a fixed natural number. The
![]() ${\mathrm {EE}} [n]$
-problem for G is the following problem: given an exponential equation over G with n variables, decide if it has a solution or not.
${\mathrm {EE}} [n]$
-problem for G is the following problem: given an exponential equation over G with n variables, decide if it has a solution or not.
By
![]() ${\mathrm {WP}}(G)$
and
${\mathrm {WP}}(G)$
and
![]() $\mathrm {CP}(G)$
, we denote the word and the conjugacy problems for G, respectively. Sometimes we omit G in these notations. We have the following relations among these decision problems:
$\mathrm {CP}(G)$
, we denote the word and the conjugacy problems for G, respectively. Sometimes we omit G in these notations. We have the following relations among these decision problems:
The first implication follows from the equivalence
![]() $ g=1\Leftrightarrow (\exists z\in \mathbb {Z})\, (g=1^z); $
the other implications are obvious. Note that the
$ g=1\Leftrightarrow (\exists z\in \mathbb {Z})\, (g=1^z); $
the other implications are obvious. Note that the
![]() ${\mathrm {EE}}\, [1]$
-problem, i.e., the problem about the solvability of equations of kind
${\mathrm {EE}}\, [1]$
-problem, i.e., the problem about the solvability of equations of kind
![]() $a^x=b$
, is called the power problem (see [Reference McCool15, Reference Ol’shanskii and Sapir20]). McCool proved in [Reference McCool15] that the implication
$a^x=b$
, is called the power problem (see [Reference McCool15, Reference Ol’shanskii and Sapir20]). McCool proved in [Reference McCool15] that the implication
![]() ${\mathrm {WP}} \Rightarrow {\mathrm {EE}}[1]$
is not valid in general in the class of recursively presented groups. Ol’shanskii and Sapir have found a finitely presented example with decidable
${\mathrm {WP}} \Rightarrow {\mathrm {EE}}[1]$
is not valid in general in the class of recursively presented groups. Ol’shanskii and Sapir have found a finitely presented example with decidable
![]() ${\mathrm {CP}} $
and undecidable
${\mathrm {CP}} $
and undecidable
![]() ${\mathrm {EE}}[1]$
(see Theorem 1.3(2) in [Reference Ol’shanskii and Sapir21]). This motivated us to raise the following problem.
${\mathrm {EE}}[1]$
(see Theorem 1.3(2) in [Reference Ol’shanskii and Sapir21]). This motivated us to raise the following problem.
Problem 1 For any
![]() $n\in \mathbb {N}\ \backslash \{ 0\}$
, construct a finitely presented group G with decidable
$n\in \mathbb {N}\ \backslash \{ 0\}$
, construct a finitely presented group G with decidable
![]() ${\mathrm {EE}} [n]$
and undecidable
${\mathrm {EE}} [n]$
and undecidable
![]() ${\mathrm {EE}} [n+1]$
.
${\mathrm {EE}} [n+1]$
.
The main result of this paper is the solution of Problem 1 for
![]() $n=1$
.
$n=1$
.
Theorem A There exists a finitely presented group with decidable
![]() ${\mathrm {EE}} [1]$
and undecidable
${\mathrm {EE}} [1]$
and undecidable
![]() ${\mathrm {EE}} [2]$
. Moreover, this group has decidable conjugacy problem.
${\mathrm {EE}} [2]$
. Moreover, this group has decidable conjugacy problem.
This theorem is proved in Sections 2 and 3.
The next issue concerns estimation of possible solutions of exponential equations over
![]() $G=\langle X\,|\, R\rangle $
by recursive functions on lengths of coefficients of these equations with respect to the generating set X. The motivation comes from the fact that this is a usual way to solve such equations. In Proposition 4.5, we show that primitive recursive functions are not sufficient for this aim. More information about the complexity of estimating functions for some interesting classes of groups can be found in Remarks 4.6 and 4.7.
$G=\langle X\,|\, R\rangle $
by recursive functions on lengths of coefficients of these equations with respect to the generating set X. The motivation comes from the fact that this is a usual way to solve such equations. In Proposition 4.5, we show that primitive recursive functions are not sufficient for this aim. More information about the complexity of estimating functions for some interesting classes of groups can be found in Remarks 4.6 and 4.7.
In Section 5, we introduce decision problems
![]() ${\mathrm {EE}}[g,G^n ]$
and
${\mathrm {EE}}[g,G^n ]$
and
![]() ${\mathrm {EE}}[G,\overline {g}]$
, which can be considered as fragments of
${\mathrm {EE}}[G,\overline {g}]$
, which can be considered as fragments of
![]() ${\mathrm {EE}}\,[n]$
for G. We show that these fragments can have diverse recursively enumerable (r.e.) Turing degrees in the same finitely presented group. From a quite general Theorem 5.3, we deduce the following statement.
${\mathrm {EE}}\,[n]$
for G. We show that these fragments can have diverse recursively enumerable (r.e.) Turing degrees in the same finitely presented group. From a quite general Theorem 5.3, we deduce the following statement.
Theorem B There exists a finitely presented torsion-free group G with decidable conjugacy problem and undecidable
![]() ${\mathrm {EE}}[1]$
such that any r.e. Turing degree is realized as the Turing degree of the problem
${\mathrm {EE}}[1]$
such that any r.e. Turing degree is realized as the Turing degree of the problem
![]() ${\mathrm { EE}}[g,G]$
for appropriate
${\mathrm { EE}}[g,G]$
for appropriate
![]() $g\in G$
.
$g\in G$
.
We use methods from combinatorial group theory and some standard facts from computability theory. We also use variants of Higman embeddings developed by Ol’shanskii and Sapir in [Reference Ol’shanskii18]–[Reference Ol’shanskii and Sapir20]. In the places where arguments are of computability theory flavor, we follow the terminology of [Reference Soare22] (in particular, we write “computable” instead of “recursive”). In the remaining parts of the paper, we keep the traditions of algorithmic group theory [Reference Lyndon and Schupp14].
The following remark is not only a warning that some terminology used in this paper differs from that by other authors, but it also leads to an interesting mathematical problem.
Remark 1.2 Using conjugations, one can rewrite the exponential equation (1.1) in the equivalent form
In [Reference Myasnikov, Nikolaev and Ushakov17], the decision problem for these equations asking about solutions in
![]() $\mathbb {Z}$
is called the integer knapsack problem (IKP). The corresponding problem for
$\mathbb {Z}$
is called the integer knapsack problem (IKP). The corresponding problem for
![]() $\mathbb {N}$
instead of
$\mathbb {N}$
instead of
![]() $\mathbb {Z}$
is called knapsack problem (KP) in analogy with the optimization problem for natural numbers. Clearly, decidability of KP
$\mathbb {Z}$
is called knapsack problem (KP) in analogy with the optimization problem for natural numbers. Clearly, decidability of KP
![]() $(G)$
implies decidability of IKP(G) (use inversions
$(G)$
implies decidability of IKP(G) (use inversions
![]() $f_i\mapsto f_i^{-1}$
). We conjecture that the converse is not valid.
$f_i\mapsto f_i^{-1}$
). We conjecture that the converse is not valid.
Problem 2 Construct a recursively presented (finitely presented) group G for which there is an algorithm deciding if a given exponential equation over G has a solution with components in
![]() $\mathbb {Z}$
, and there is no algorithm deciding the analogous question about solutions with components in
$\mathbb {Z}$
, and there is no algorithm deciding the analogous question about solutions with components in
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
In our paper, we will often work with equations of the form (1.2) instead of (1.1).
2 A recursively presented group with decidable
 ${\mathrm {EE}}[1]$
and undecidable
${\mathrm {EE}}[1]$
and undecidable
 ${\mathrm {EE}}[2]$
${\mathrm {EE}}[2]$
When G is a group given by a recursive presentation
![]() $\langle X\,|\ R\rangle $
and
$\langle X\,|\ R\rangle $
and
![]() $w\in G$
, we denote by
$w\in G$
, we denote by
![]() $|w|_X$
the length of a shortest word in the alphabet
$|w|_X$
the length of a shortest word in the alphabet
![]() $X\cup X^{-1}$
representing w. The free group generated by X is denoted by
$X\cup X^{-1}$
representing w. The free group generated by X is denoted by
![]() ${\mathrm {F}} (X)$
. The length of
${\mathrm {F}} (X)$
. The length of
![]() $u\in {\mathrm {F}}(X)$
with respect to X will be often written as
$u\in {\mathrm {F}}(X)$
with respect to X will be often written as
![]() $|u|$
. A syllable of u is a maximal subword of the form
$|u|$
. A syllable of u is a maximal subword of the form
![]() $x^k$
,
$x^k$
,
![]() $k\in \mathbb {Z}$
, where
$k\in \mathbb {Z}$
, where
![]() $x\in X$
. When the word u is cyclically reduced, it can be viewed as a cyclic word, i.e., the set of all cyclic shifts of u.
$x\in X$
. When the word u is cyclically reduced, it can be viewed as a cyclic word, i.e., the set of all cyclic shifts of u.
The main purpose of this section is the following weaker version of Theorem A.
Proposition 2.1 There exists a recursively presented group G such that
![]() ${\mathrm {EE}}[1]$
is decidable, but
${\mathrm {EE}}[1]$
is decidable, but
![]() ${\mathrm {EE}}[2]$
is undecidable.
${\mathrm {EE}}[2]$
is undecidable.
In the proof of this proposition, we use the following lemmas. The first one is obvious.
Lemma 2.2 Let w and u be two nontrivial elements of the free group
![]() ${\mathrm {F}}(X)$
. If
${\mathrm {F}}(X)$
. If
![]() $w=u^z$
for some
$w=u^z$
for some
![]() $z\in \mathbb {Z}$
, then
$z\in \mathbb {Z}$
, then
![]() $|z|\leqslant |w|_X$
.
$|z|\leqslant |w|_X$
.
Lemma 2.3 Let
![]() $w(a,b,c)$
be a nonempty reduced cyclic word in
$w(a,b,c)$
be a nonempty reduced cyclic word in
![]() ${\mathrm {F}}(a,b,c)$
, and let
${\mathrm {F}}(a,b,c)$
, and let
Suppose that
![]() $m>M$
. Then
$m>M$
. Then
![]() $w(a,b,a^mb^m)\neq 1$
in
$w(a,b,a^mb^m)\neq 1$
in
![]() ${\mathrm {F}}(a,b)$
. Moreover, if
${\mathrm {F}}(a,b)$
. Moreover, if
for some
![]() $v(a,b)\in {\mathrm {F}}(a,b)$
and
$v(a,b)\in {\mathrm {F}}(a,b)$
and
![]() $z\in \mathbb {Z}$
, then
$z\in \mathbb {Z}$
, then
![]() $|z|\leqslant |w(a,b,c)|$
.
$|z|\leqslant |w(a,b,c)|$
.
Proof We assume that w contains at least one c or
![]() $c^{-1}$
(otherwise the statement is obvious).
$c^{-1}$
(otherwise the statement is obvious).
After substitution
![]() $c \rightarrow a^mb^m$
, the word w is uniquely factorized as
$c \rightarrow a^mb^m$
, the word w is uniquely factorized as
![]() $w_0 w_1 \ldots w_k$
where every
$w_0 w_1 \ldots w_k$
where every
![]() $w_i$
with
$w_i$
with
![]() $i \notin \{ 0,k\}$
has one of the following forms for a reduced
$i \notin \{ 0,k\}$
has one of the following forms for a reduced
![]() ${u_i =u_i (a,b)}$
:
${u_i =u_i (a,b)}$
:
-
1.
 $b^m u_i a^m$
,
$b^m u_i a^m$
, -
2.
 $a^{-m} u_i b^{-m}$
,
$a^{-m} u_i b^{-m}$
, -
3.
 $b^m u_i b^{-m}$
,
$b^m u_i b^{-m}$
, -
4.
 $a^{-m} u_i a^m$
.
$a^{-m} u_i a^m$
.
The word
![]() $w_0$
(resp.
$w_0$
(resp.
![]() $w_k$
) has the same form except that the initial (final) syllable
$w_k$
) has the same form except that the initial (final) syllable
![]() $b^m$
or
$b^m$
or
![]() $a^{-m}$
(resp.
$a^{-m}$
(resp.
![]() $a^m$
or
$a^m$
or
![]() $b^{-m}$
) is missing. Note that in cases 3 and 4, the word
$b^{-m}$
) is missing. Note that in cases 3 and 4, the word
![]() $u_i$
cannot be empty; otherwise, w would not be reduced.
$u_i$
cannot be empty; otherwise, w would not be reduced.
Since
![]() $u_i$
contains no exponent larger than M, the reduced normal form
$u_i$
contains no exponent larger than M, the reduced normal form
![]() $\mathsf {red}(w_i)$
for
$\mathsf {red}(w_i)$
for
![]() $i\notin \{ 0,k\}$
is as follows. In case 1, it is of the form
$i\notin \{ 0,k\}$
is as follows. In case 1, it is of the form
![]() $b\ldots a$
; in case 2, it is of the form
$b\ldots a$
; in case 2, it is of the form
![]() $a^{-1} \ldots b^{-1}$
; and in case 3, it is of the form
$a^{-1} \ldots b^{-1}$
; and in case 3, it is of the form
![]() $b\ldots b^{-1}$
provided
$b\ldots b^{-1}$
provided
![]() $u_i$
contains an a-syllable. When
$u_i$
contains an a-syllable. When
![]() $u_i$
does not contain an a-syllable,
$u_i$
does not contain an a-syllable,
![]() $\mathsf {red}(w_i)= b^r$
, where
$\mathsf {red}(w_i)= b^r$
, where
![]() $1 \le |r| <M$
. Case 4 is similar to case 3 (with a instead of b).
$1 \le |r| <M$
. Case 4 is similar to case 3 (with a instead of b).
Applying this analysis (with natural versions of it in the cases of
![]() $w_0$
and
$w_0$
and
![]() $w_k$
) and using the observation that if
$w_k$
) and using the observation that if
![]() $w_i$
ends with
$w_i$
ends with
![]() $a^m$
(resp.
$a^m$
(resp.
![]() $b^{-m}$
) then
$b^{-m}$
) then
![]() $w_{i+1}$
starts with
$w_{i+1}$
starts with
![]() $b^m$
(resp.
$b^m$
(resp.
![]() $a^{-m}$
), we see that
$a^{-m}$
), we see that
Thus,
![]() $\mathsf {red}(w(a,b,a^mb^m))$
has at least two syllables, i.e., it is not empty.
$\mathsf {red}(w(a,b,a^mb^m))$
has at least two syllables, i.e., it is not empty.
For the second statement of the lemma, we may assume that
![]() $v(a,b)$
is cyclically reduced and when it starts with
$v(a,b)$
is cyclically reduced and when it starts with
![]() $a^{\pm 1}$
(resp.
$a^{\pm 1}$
(resp.
![]() $b^{\pm 1}$
), then it ends with
$b^{\pm 1}$
), then it ends with
![]() $b^{\pm 1}$
(resp.
$b^{\pm 1}$
(resp.
![]() $a^{\pm 1}$
). This can be achieved using conjugations. Let
$a^{\pm 1}$
). This can be achieved using conjugations. Let
![]() $n_1$
be the number of syllables in
$n_1$
be the number of syllables in
![]() $\mathsf {red}(w(a,b,a^mb^m))$
, and let
$\mathsf {red}(w(a,b,a^mb^m))$
, and let
![]() $n_2$
be the number of syllables in
$n_2$
be the number of syllables in
![]() $v(a,b)$
. Then
$v(a,b)$
. Then
![]() $\mathsf {min}(n_1 ,n_2 )\geqslant 2$
and
$\mathsf {min}(n_1 ,n_2 )\geqslant 2$
and
![]() $z=n_1/n_2\leqslant n_1/2$
. It remains to note that
$z=n_1/n_2\leqslant n_1/2$
. It remains to note that
![]() $n_1\leqslant 2|w(a,b,c)|$
. The latter is valid since, after substitution
$n_1\leqslant 2|w(a,b,c)|$
. The latter is valid since, after substitution
![]() $c\rightarrow a^mb^m$
in w, the total number of a-syllables and b-syllables increases by at most
$c\rightarrow a^mb^m$
in w, the total number of a-syllables and b-syllables increases by at most
![]() $2k$
, where k is the number of occurrences of
$2k$
, where k is the number of occurrences of
![]() $c^{\pm 1}$
in w.
$c^{\pm 1}$
in w.
Proof of Proposition 2.1
Our construction resembles McCool’s example from [Reference McCool15]. Let
![]() $f:\mathbb {N}\rightarrow \mathbb {N}$
be a one-to-one recursive function with nonrecursive range. Consider the following infinite presentation:
$f:\mathbb {N}\rightarrow \mathbb {N}$
be a one-to-one recursive function with nonrecursive range. Consider the following infinite presentation:
Let
![]() $X=\underset {i\in \mathbb {N}}\cup X_i$
, where
$X=\underset {i\in \mathbb {N}}\cup X_i$
, where
![]() $X_i=\{a_i,b_i,c_i\}$
. Let
$X_i=\{a_i,b_i,c_i\}$
. Let
![]() $H_i$
be the subgroup of G generated by
$H_i$
be the subgroup of G generated by
![]() $X_i$
. Then
$X_i$
. Then
where each
![]() $H_j$
is free and
$H_j$
is free and
 $$ \begin{align*} \mathrm{rk}(H_j)= \begin{cases} 2, & \hspace{2mm} {{\mathrm{if}}}\hspace{2mm} j\in {\mathrm{im}} f,\\ 3, & \hspace{2mm} {{\mathrm{if}}}\hspace{2mm} j\notin {\mathrm{im}} f. \end{cases} \end{align*} $$
$$ \begin{align*} \mathrm{rk}(H_j)= \begin{cases} 2, & \hspace{2mm} {{\mathrm{if}}}\hspace{2mm} j\in {\mathrm{im}} f,\\ 3, & \hspace{2mm} {{\mathrm{if}}}\hspace{2mm} j\notin {\mathrm{im}} f. \end{cases} \end{align*} $$
Claim 1 The word problem is decidable for the presentation (2.1).
Proof Using the normal form of an element of the free product (2.2), we reduce
![]() $\mathrm {WP} (G)$
to the following problem. Given
$\mathrm {WP} (G)$
to the following problem. Given
![]() $j\in \mathbb {N}$
and given a reduced nonempty word
$j\in \mathbb {N}$
and given a reduced nonempty word
![]() $w(a_j,b_j,c_j)$
, decide whether the corresponding element of
$w(a_j,b_j,c_j)$
, decide whether the corresponding element of
![]() $H_j$
is trivial or not. The difficulty is that we do not know whether
$H_j$
is trivial or not. The difficulty is that we do not know whether
![]() $j\in \mathrm {im} (f)$
or not.
$j\in \mathrm {im} (f)$
or not.
From now on, we consider
![]() $w(a_j,b_j,c_j)$
as a nonempty reduced cyclic word in
$w(a_j,b_j,c_j)$
as a nonempty reduced cyclic word in
![]() ${\mathrm {F}}(a_j,b_j,c_j)$
. Let M be the maximum of absolute values of exponents of
${\mathrm {F}}(a_j,b_j,c_j)$
. Let M be the maximum of absolute values of exponents of
![]() $a_j$
and
$a_j$
and
![]() $b_j$
in the word
$b_j$
in the word
![]() $w(a_j,b_j,c_j)$
.
$w(a_j,b_j,c_j)$
.
First, we verify whether there exists
![]() $m\leqslant M$
with
$m\leqslant M$
with
![]() $j = f(m)$
or not. If such m exists, we substitute
$j = f(m)$
or not. If such m exists, we substitute
![]() $a_j^m b_j^m$
for
$a_j^m b_j^m$
for
![]() $c_j$
in
$c_j$
in
![]() $w(a_j,b_j,c_j)$
and verify whether the resulting word is trivial in
$w(a_j,b_j,c_j)$
and verify whether the resulting word is trivial in
![]() ${\mathrm {F}}(a_j,b_j)$
or not. This can be done effectively.
${\mathrm {F}}(a_j,b_j)$
or not. This can be done effectively.
We claim that, in the remaining cases, the word w is nontrivial in G. Indeed, if
![]() $j\notin \mathrm {im} f$
, then
$j\notin \mathrm {im} f$
, then
![]() $H_j\cong {\mathrm {F}}(a_j,b_j,c_j)$
, and hence
$H_j\cong {\mathrm {F}}(a_j,b_j,c_j)$
, and hence
![]() $w(a_j,b_j,c_j)$
is nontrivial in
$w(a_j,b_j,c_j)$
is nontrivial in
![]() $H_j$
. If
$H_j$
. If
![]() $j=f(m)$
for some
$j=f(m)$
for some
![]() $m>M$
, then
$m>M$
, then
![]() $w(a_j,b_j,c_j)=w(a_j,b_j,a_j^mb_j^m)$
is nontrivial in
$w(a_j,b_j,c_j)=w(a_j,b_j,a_j^mb_j^m)$
is nontrivial in
![]() ${\mathrm {F}}(a_j,b_j)$
by Lemma 2.3.
${\mathrm {F}}(a_j,b_j)$
by Lemma 2.3.
Claim 2 The group G has undecidable
![]() ${\mathrm {EE}}[2]$
.
${\mathrm {EE}}[2]$
.
Proof The equation
![]() $c_k=a_k^xb_k^y$
is solvable if and only if
$c_k=a_k^xb_k^y$
is solvable if and only if
![]() $k=f(i)$
for some i (in this case,
$k=f(i)$
for some i (in this case,
![]() $x=y=i$
is the unique solution). Since the set
$x=y=i$
is the unique solution). Since the set
![]() $\mathrm {im} (f)$
is not recursive, we cannot recognize whether such i exists or not. Therefore, we cannot recognize the existence of such x and y.
$\mathrm {im} (f)$
is not recursive, we cannot recognize whether such i exists or not. Therefore, we cannot recognize the existence of such x and y.
Claim 3 The group G has decidable
![]() ${\mathrm {EE}}[1]$
.
${\mathrm {EE}}[1]$
.
Proof Consider an exponential equation
where u and v are nontrivial words in the alphabet
![]() $X=\underset {i\in \mathbb {N}}{\cup } X_i$
. In order to decide if it is solvable, we may assume that
$X=\underset {i\in \mathbb {N}}{\cup } X_i$
. In order to decide if it is solvable, we may assume that
![]() $u\neq 1$
and
$u\neq 1$
and
![]() $v\neq 1$
in G.
$v\neq 1$
in G.
We write
![]() $v=v_1v_2\dots v_{\ell }$
, where
$v=v_1v_2\dots v_{\ell }$
, where
![]() $v_i$
is a word in the alphabet
$v_i$
is a word in the alphabet
![]() $X_{\lambda (i)}$
for some
$X_{\lambda (i)}$
for some
![]() $\lambda (i)$
,
$\lambda (i)$
,
![]() $i=1,\dots ,\ell $
, and
$i=1,\dots ,\ell $
, and
![]() $\lambda (j)\neq \lambda (j+1)$
for
$\lambda (j)\neq \lambda (j+1)$
for
![]() $j=1,\dots ,\ell -1$
. Moreover (using decidability of
$j=1,\dots ,\ell -1$
. Moreover (using decidability of
![]() $\mathrm {WP}(G)$
), we assume that each
$\mathrm {WP}(G)$
), we assume that each
![]() $v_i$
represents a nontrivial element of
$v_i$
represents a nontrivial element of
![]() $H_{\lambda (i)}$
. Using conjugation, we may additionally assume that
$H_{\lambda (i)}$
. Using conjugation, we may additionally assume that
![]() $\lambda (1)\neq \lambda (\ell )$
if
$\lambda (1)\neq \lambda (\ell )$
if
![]() $\ell>1$
. Analogously, we write
$\ell>1$
. Analogously, we write
![]() $u=u_1 u_2\dots u_{k}$
. Note that
$u=u_1 u_2\dots u_{k}$
. Note that
![]() $v_1$
and
$v_1$
and
![]() $u_1$
(resp.
$u_1$
(resp.
![]() $v_{\ell }$
and
$v_{\ell }$
and
![]() $u_k$
) belong to the same subgroup
$u_k$
) belong to the same subgroup
![]() $H_j$
.
$H_j$
.
Suppose that
![]() $\ell>1$
. Then a necessary condition for solvability of equation (2.3) is
$\ell>1$
. Then a necessary condition for solvability of equation (2.3) is
![]() $k>1$
. If this condition is fulfilled, then any possible solution z of equation (2.3) satisfies
$k>1$
. If this condition is fulfilled, then any possible solution z of equation (2.3) satisfies
![]() $|z|=k/\ell $
, and the existence of a solution z can be verified using decidability of
$|z|=k/\ell $
, and the existence of a solution z can be verified using decidability of
![]() $\mathrm {WP}(G)$
.
$\mathrm {WP}(G)$
.
Let
![]() $\ell =1$
. Then a necessary condition for solvability of equation (2.3) is
$\ell =1$
. Then a necessary condition for solvability of equation (2.3) is
![]() $k=1$
. Thus, we assume that
$k=1$
. Thus, we assume that
![]() $u,v$
are words in the alphabet
$u,v$
are words in the alphabet
![]() $X_j$
for some j. We want to solve the equation
$X_j$
for some j. We want to solve the equation
Without loss of generality, we assume that
![]() $u(a_j,b_j,c_j)$
is a reduced cyclic word. Let M be the maximum of absolute values of exponents of
$u(a_j,b_j,c_j)$
is a reduced cyclic word. Let M be the maximum of absolute values of exponents of
![]() $a_j$
and
$a_j$
and
![]() $b_j$
in
$b_j$
in
![]() $u(a_j,b_j,c_j)$
.
$u(a_j,b_j,c_j)$
.
First, we check whether some
![]() $m\in \{1,\dots ,M\}$
satisfies
$m\in \{1,\dots ,M\}$
satisfies
![]() $f(m)=j$
. If such m is found, equation (2.4) takes the form
$f(m)=j$
. If such m is found, equation (2.4) takes the form
and the solvability of this equation can be verified with the help of Lemma 2.2.
If no such m exists, then either
![]() $j\notin \mathrm {im} f$
, or
$j\notin \mathrm {im} f$
, or
![]() $j=f(m)$
for some
$j=f(m)$
for some
![]() $m>M$
. We claim that, in these cases, the absolute value of a possible solution z of equation (2.4) does not exceed the length of the word
$m>M$
. We claim that, in these cases, the absolute value of a possible solution z of equation (2.4) does not exceed the length of the word
![]() $u(a_j,b_j,c_j)$
in
$u(a_j,b_j,c_j)$
in
![]() ${\mathrm {F}}(a_j ,b_j ,c_j )$
. Indeed, if
${\mathrm {F}}(a_j ,b_j ,c_j )$
. Indeed, if
![]() $j\notin \mathrm {im} f$
, then
$j\notin \mathrm {im} f$
, then
![]() $H_j$
is the free group with basis
$H_j$
is the free group with basis
![]() $\{a_j,b_j,c_j\}$
, and the claim follows from Lemma 2.2. If
$\{a_j,b_j,c_j\}$
, and the claim follows from Lemma 2.2. If
![]() $j\in \mathrm {im} f$
, then the claim follows from Lemma 2.3.
$j\in \mathrm {im} f$
, then the claim follows from Lemma 2.3.
Using the estimation for
![]() $|z|$
and decidability of
$|z|$
and decidability of
![]() $\mathrm {WP}(G)$
, we can verify whether equation (2.4) has a solution.
$\mathrm {WP}(G)$
, we can verify whether equation (2.4) has a solution.
3 Proof of Theorem A
Below, we deduce Theorem A from Proposition 2.1 and the following result of Ol’shanskii and Sapir.
Theorem 3.1 (See [Reference Ol’shanskii and Sapir20, Theorem 1])
Every countable group
![]() $G=\langle x_1,x_2,\dots \,|\, R\rangle $
with solvable power problem is embeddable into a 2-generated finitely presented group
$G=\langle x_1,x_2,\dots \,|\, R\rangle $
with solvable power problem is embeddable into a 2-generated finitely presented group
![]() $\overline {G}=\langle y_1,y_2\,|\, \overline {R}\rangle $
with solvable conjugacy and power problems.
$\overline {G}=\langle y_1,y_2\,|\, \overline {R}\rangle $
with solvable conjugacy and power problems.
Remark 3.2 In this remark, we recall the main steps of the proof of Theorem 3.1. We do this to make clear that the embedding
![]() $\varphi : G\rightarrow \overline {G}$
constructed in the proof of this theorem is computable. This means that there exists an algorithm, which, given
$\varphi : G\rightarrow \overline {G}$
constructed in the proof of this theorem is computable. This means that there exists an algorithm, which, given
![]() $i\in \mathbb {N}$
, expresses
$i\in \mathbb {N}$
, expresses
![]() $x_i$
as a word in
$x_i$
as a word in
![]() $y_1$
and
$y_1$
and
![]() $y_2$
. Furthermore, these steps will be also used in arguments of Sections 4 and 5.
$y_2$
. Furthermore, these steps will be also used in arguments of Sections 4 and 5.
Four steps in the construction of Ol’shanskii and Sapir. Before we start, observe that any countable group
![]() $G=\langle x_1,x_2,\dots \,|\, R \rangle $
with solvable power problem has solvable word problem; hence, it admits a recursive presentation. Thus, we may assume that the given presentation of G is recursive. Moreover, the solvability of power problem implies the solvability of order problem (there exists an algorithm which computes orders of elements).
$G=\langle x_1,x_2,\dots \,|\, R \rangle $
with solvable power problem has solvable word problem; hence, it admits a recursive presentation. Thus, we may assume that the given presentation of G is recursive. Moreover, the solvability of power problem implies the solvability of order problem (there exists an algorithm which computes orders of elements).
Step 1. In [Reference Donald3], Collins noticed that if H is a recursively presented group with solvable power problem and
![]() $a,b$
are two elements in H of the same order, then the HNN extension
$a,b$
are two elements in H of the same order, then the HNN extension
![]() $H_{a,b}=\langle H,t\,|\, t^{-1}at=b\rangle $
has solvable power problem.
$H_{a,b}=\langle H,t\,|\, t^{-1}at=b\rangle $
has solvable power problem.
Using a sequence of HNN extensions of this type, G can be embedded into a recursively presented group
![]() $G_1$
with solvable power problem where every two elements of the same order are conjugate. Thus, the conjugacy problem in
$G_1$
with solvable power problem where every two elements of the same order are conjugate. Thus, the conjugacy problem in
![]() $G_1$
is decidable. Moreover, the constructed embedding
$G_1$
is decidable. Moreover, the constructed embedding
![]() $\varphi _1:G\rightarrow G_1$
(the identity map on the generators of G) is computable.
$\varphi _1:G\rightarrow G_1$
(the identity map on the generators of G) is computable.
Step 2. In [Reference Ol’shanskii18], Ol’shanskii suggested the following construction for embedding of countable groups into 2-generated groups. Let
![]() $H=\langle x_1,x_2,\dots \, |\, \mathcal {R}\rangle $
be any countable group. Denote by
$H=\langle x_1,x_2,\dots \, |\, \mathcal {R}\rangle $
be any countable group. Denote by
![]() $\mathcal {R}_1$
the set of words in the alphabet
$\mathcal {R}_1$
the set of words in the alphabet
![]() $\{a,b\}$
obtained by substituting the word
$\{a,b\}$
obtained by substituting the word
for every
![]() $x_i$
in every word from
$x_i$
in every word from
![]() $\mathcal {R}$
. It was shown in [Reference Ol’shanskii18] that the map
$\mathcal {R}$
. It was shown in [Reference Ol’shanskii18] that the map
![]() $x_i\mapsto A_i$
,
$x_i\mapsto A_i$
,
![]() $i\in \mathbb {N}$
, extends to an embedding of H into
$i\in \mathbb {N}$
, extends to an embedding of H into
![]() $H_1=\langle a,b\,|\, \mathcal {R}_1\rangle $
. Lemmas 10 and 11 of [Reference Ol’shanskii and Sapir20] say that if the group H has decidable word or conjugacy problem or power problem, then the same problem is decidable for the group
$H_1=\langle a,b\,|\, \mathcal {R}_1\rangle $
. Lemmas 10 and 11 of [Reference Ol’shanskii and Sapir20] say that if the group H has decidable word or conjugacy problem or power problem, then the same problem is decidable for the group
![]() $H_1$
.
$H_1$
.
Applying this construction, we obtain a computable embedding
![]() $\varphi _2:G_1\rightarrow G_2$
, where
$\varphi _2:G_1\rightarrow G_2$
, where
![]() $G_2=\langle a,b\,|\, R_2\rangle $
is 2-generated, recursively presented, and has solvable power and conjugacy problems.
$G_2=\langle a,b\,|\, R_2\rangle $
is 2-generated, recursively presented, and has solvable power and conjugacy problems.
Step 3. Lemma 12 of [Reference Ol’shanskii and Sapir20] says that this
![]() $G_2$
can be embedded into a finitely presented group
$G_2$
can be embedded into a finitely presented group
![]() $G_3=\langle a,b, c_1,\dots ,c_n\,|\, R_3\rangle $
with solvable power and conjugacy problems. This embedding extends the identity map
$G_3=\langle a,b, c_1,\dots ,c_n\,|\, R_3\rangle $
with solvable power and conjugacy problems. This embedding extends the identity map
![]() $a\mapsto a$
,
$a\mapsto a$
,
![]() $b\mapsto b$
, which is obviously computable.
$b\mapsto b$
, which is obviously computable.
The corresponding embedding was first described in [Reference Ol’shanskii and Sapir19]. We indicate that
![]() $G_2$
and
$G_2$
and
![]() $G_3$
play the roles of K and H in [Reference Ol’shanskii and Sapir19].
$G_3$
play the roles of K and H in [Reference Ol’shanskii and Sapir19].
Step 4. Using the construction from Step 2 once more, we embed
![]() $G_3$
into a 2-generated finitely presented group
$G_3$
into a 2-generated finitely presented group
![]() $\overline {G}=\langle y_1,y_2\,|\, \overline {R}\rangle $
with solvable conjugacy and power problems.
$\overline {G}=\langle y_1,y_2\,|\, \overline {R}\rangle $
with solvable conjugacy and power problems.
Since the embeddings at all steps are computable, their composition
![]() $\varphi :G\rightarrow \overline {G}$
is computable as well.
$\varphi :G\rightarrow \overline {G}$
is computable as well.
Proof of Theorem A
By Proposition 2.1, there is a recursively presented group G with decidable
![]() ${\mathrm {EE}}[1]$
and undecidable
${\mathrm {EE}}[1]$
and undecidable
![]() ${\mathrm {EE}}[2]$
. Using Theorem 3.1 and Remark 3.2, we obtain a computable embedding
${\mathrm {EE}}[2]$
. Using Theorem 3.1 and Remark 3.2, we obtain a computable embedding
![]() $\varphi :G\rightarrow \overline {G}$
, where
$\varphi :G\rightarrow \overline {G}$
, where
![]() $\overline {G}$
is finitely presented and has decidable
$\overline {G}$
is finitely presented and has decidable
![]() ${\mathrm {EE}}[1]$
. Since
${\mathrm {EE}}[1]$
. Since
![]() $\varphi $
is computable, undecidability of
$\varphi $
is computable, undecidability of
![]() ${\mathrm {EE}}[2]$
for G implies undecidability of
${\mathrm {EE}}[2]$
for G implies undecidability of
![]() ${\mathrm {EE}}[2]$
for
${\mathrm {EE}}[2]$
for
![]() $\overline {G}$
.
$\overline {G}$
.
Indeed, consider an arbitrary equation
![]() $g_0=g_1^xg_2^y$
with
$g_0=g_1^xg_2^y$
with
![]() $g_0,g_1,g_2\in G$
written as words in the generators of G. Using computability of
$g_0,g_1,g_2\in G$
written as words in the generators of G. Using computability of
![]() $\varphi $
, we can write
$\varphi $
, we can write
![]() $\varphi (g_0)$
,
$\varphi (g_0)$
,
![]() $\varphi (g_1)$
,
$\varphi (g_1)$
,
![]() $\varphi (g_2)$
as words in the generators of
$\varphi (g_2)$
as words in the generators of
![]() $\overline {G}$
. The equation
$\overline {G}$
. The equation
![]() $\varphi (g_0)=\varphi (g_1)^x\varphi (g_2)^y$
has the same solutions as the original one. If we could decide whether this equation is solvable, we could decide whether the original equation is solvable. However,
$\varphi (g_0)=\varphi (g_1)^x\varphi (g_2)^y$
has the same solutions as the original one. If we could decide whether this equation is solvable, we could decide whether the original equation is solvable. However,
![]() ${\mathrm {EE}}[2]$
is undecidable for G. Hence, it is undecidable for
${\mathrm {EE}}[2]$
is undecidable for G. Hence, it is undecidable for
![]() $\overline {G}$
.
$\overline {G}$
.
Remark 3.3 The Knapsack counterpart of
![]() ${\mathrm {EE}} [2]$
is also undecidable in
${\mathrm {EE}} [2]$
is also undecidable in
![]() $\overline {G}$
.
$\overline {G}$
.
4 Estimating functions for solutions of exponential equations
Let G be a group generated by a set X. For any finite tuple
![]() $\bar {g}=(g_0,\dots ,g_n)$
of elements of G, the
$\bar {g}=(g_0,\dots ,g_n)$
of elements of G, the
![]() $\infty $
-norm of this tuple is the number
$\infty $
-norm of this tuple is the number
In the case where
![]() $G=\mathbb {Z}$
and
$G=\mathbb {Z}$
and
![]() $X=\{1\}$
, we omit X and write
$X=\{1\}$
, we omit X and write
![]() $\|\bar {g}\|$
.
$\|\bar {g}\|$
.
Definition 4.1 Let G be a group generated by a set X. A function
![]() $f:\mathbb {N}\rightarrow \mathbb {N}$
is called an
$f:\mathbb {N}\rightarrow \mathbb {N}$
is called an
![]() ${\mathrm {EE}}[n]$
-estimating function for G (with respect to X) if for any exponential equation
${\mathrm {EE}}[n]$
-estimating function for G (with respect to X) if for any exponential equation
![]() $g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
over G with nonempty set of solutions, there exists a solution
$g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
over G with nonempty set of solutions, there exists a solution
![]() $\bar {k}=(k_1,\dots ,k_n)$
with
$\bar {k}=(k_1,\dots ,k_n)$
with
Remark 4.2 Let G be a group, and let X and Y be two generating sets of G. Suppose that
If there exists a (recursive)
![]() ${\mathrm {EE}}[n]$
-estimating function for G with respect to X, then there exists a (recursive)
${\mathrm {EE}}[n]$
-estimating function for G with respect to X, then there exists a (recursive)
![]() ${\mathrm {EE}}[n]$
-estimating function for G with respect to Y.
${\mathrm {EE}}[n]$
-estimating function for G with respect to Y.
The following lemma relates decidability of
![]() ${\mathrm {EE}}[n]$
in G and existence of a total recursive
${\mathrm {EE}}[n]$
in G and existence of a total recursive
![]() ${\mathrm {EE}}[n]$
-estimating function. It is a counterpart of the fact that a group G with a finite generating set X has solvable
${\mathrm {EE}}[n]$
-estimating function. It is a counterpart of the fact that a group G with a finite generating set X has solvable
![]() $\mathrm {WP}$
if and only if the Dehn function of G with respect to X is total recursive.
$\mathrm {WP}$
if and only if the Dehn function of G with respect to X is total recursive.
Lemma 4.3 Let G be a group generated by a finite set X. For any
![]() $n\in \mathbb {N}$
, the following two conditions are equivalent.
$n\in \mathbb {N}$
, the following two conditions are equivalent.
-
(1)
 ${\mathrm {EE}}[n]$
is decidable in G.
${\mathrm {EE}}[n]$
is decidable in G. -
(2)
 $\mathrm {WP}(G)$
is decidable, and there exists a total recursive
$\mathrm {WP}(G)$
is decidable, and there exists a total recursive
 ${\mathrm {EE}}[n]$
-estimating function for G with respect to X.
${\mathrm {EE}}[n]$
-estimating function for G with respect to X.
Proof
![]() $(1)\Rightarrow (2)$
. Suppose that
$(1)\Rightarrow (2)$
. Suppose that
![]() ${\mathrm {EE}}[n]$
is decidable in G. Then, clearly,
${\mathrm {EE}}[n]$
is decidable in G. Then, clearly,
![]() $\mathrm {WP}(G)$
is decidable. Now, we define the desired function
$\mathrm {WP}(G)$
is decidable. Now, we define the desired function
![]() $f:\mathbb {N}\rightarrow \mathbb {N}$
at arbitrary point
$f:\mathbb {N}\rightarrow \mathbb {N}$
at arbitrary point
![]() $m\in \mathbb {N}$
in four steps.
$m\in \mathbb {N}$
in four steps.
-
(1) Let
 $B(m)$
be the set of all tuples
$B(m)$
be the set of all tuples
 $\bar {g}=(g_0,g_1,\dots ,g_n)$
of words in the alphabet X satisfying
$\bar {g}=(g_0,g_1,\dots ,g_n)$
of words in the alphabet X satisfying
 $\|\bar {g}\|_X\leqslant m$
. Since X is finite, the set
$\|\bar {g}\|_X\leqslant m$
. Since X is finite, the set
 $B(m)$
is finite and we can compute it.
$B(m)$
is finite and we can compute it. -
(2) Let
 $B(m)'$
be the subset of
$B(m)'$
be the subset of
 $B(m)$
consisting of the tuples
$B(m)$
consisting of the tuples
 $\bar {g}=(g_0,g_1,\dots ,g_n)$
for which the equation
$\bar {g}=(g_0,g_1,\dots ,g_n)$
for which the equation
 $g_0 = g^{x_1}_{1} \cdot \cdots \cdot g^{x_n}_n$
has a solution. We can compute
$g_0 = g^{x_1}_{1} \cdot \cdots \cdot g^{x_n}_n$
has a solution. We can compute
 $B(m)'$
using decidability of
$B(m)'$
using decidability of
 ${\mathrm {EE}}[n]$
in G. Note
${\mathrm {EE}}[n]$
in G. Note
 $(1,\ldots ,1) \in B(m)'$
.
$(1,\ldots ,1) \in B(m)'$
. -
(3) For each tuple
 $\bar {g}\in B(m)'$
, we can find some solution
$\bar {g}\in B(m)'$
, we can find some solution
 $\bar {k}=(k_1,\dots ,k_n)$
of the equation
$\bar {k}=(k_1,\dots ,k_n)$
of the equation
 $g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
using an effective enumeration of n-tuples of integers and the decidability of
$g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
using an effective enumeration of n-tuples of integers and the decidability of
 $\mathrm {WP}(G)$
. We denote this solution by
$\mathrm {WP}(G)$
. We denote this solution by
 $\bar {k}(\bar {g})$
. When
$\bar {k}(\bar {g})$
. When
 $\bar {g} = \bar {1}$
, we put
$\bar {g} = \bar {1}$
, we put
 $\bar {k}(\bar {g})= \bar {1}$
.
$\bar {k}(\bar {g})= \bar {1}$
. -
(4) Finally, we set
 $f(m)$
to be the maximum of
$f(m)$
to be the maximum of
 $\|\bar {k}(\bar {g})\|$
over all
$\|\bar {k}(\bar {g})\|$
over all
 $\bar {g}\in B(m)'$
.
$\bar {g}\in B(m)'$
.
The function f is total recursive and satisfies Definition 4.1.
![]() $(2)\Rightarrow (1)$
. Consider an exponential equation
$(2)\Rightarrow (1)$
. Consider an exponential equation
![]() $g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
over G. To decide whether this equation has a solution, we verify whether the equality
$g_0 = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
over G. To decide whether this equation has a solution, we verify whether the equality
![]() $g_0 = g^{k_1}_{1} \cdot \cdots \cdot g^{k_n}_n$
holds for at least one tuple
$g_0 = g^{k_1}_{1} \cdot \cdots \cdot g^{k_n}_n$
holds for at least one tuple
![]() $\bar {k}=(k_1,\dots ,k_n)\in \mathbb {Z}^n$
with
$\bar {k}=(k_1,\dots ,k_n)\in \mathbb {Z}^n$
with
![]() $\|\bar {k}\|\leqslant f(\|\bar {g}\|_X)$
. The verification for a concrete tuple
$\|\bar {k}\|\leqslant f(\|\bar {g}\|_X)$
. The verification for a concrete tuple
![]() $\bar {k}$
can be done using
$\bar {k}$
can be done using
![]() $\mathrm {WP}(G)$
.
$\mathrm {WP}(G)$
.
Remark 4.4 In [Reference Kharlampovich8], Kharlampovich constructed a group G which is finitely presented in the variety
![]() $x^m=1$
and has undecidable word problem. By Lemma 4.3,
$x^m=1$
and has undecidable word problem. By Lemma 4.3,
![]() ${\mathrm {EE}}[n]$
is undecidable for each n. On the other hand, the constant function
${\mathrm {EE}}[n]$
is undecidable for each n. On the other hand, the constant function
![]() $f(k) = m$
,
$f(k) = m$
,
![]() $k\in \mathbb {N}$
, is a total recursive
$k\in \mathbb {N}$
, is a total recursive
![]() ${\mathrm {EE}}[n]$
-estimating function for G.
${\mathrm {EE}}[n]$
-estimating function for G.
The following proposition shows that there is a finitely presented group with decidable
![]() ${\mathrm {EE}}[1]$
which does not have a primitive recursive
${\mathrm {EE}}[1]$
which does not have a primitive recursive
![]() ${\mathrm {EE}}[1]$
-estimating function.
${\mathrm {EE}}[1]$
-estimating function.
Proposition 4.5 There exists a finitely presented group
![]() $G = \langle X |\, \mathcal {R}\rangle $
with decidable
$G = \langle X |\, \mathcal {R}\rangle $
with decidable
![]() ${\mathrm {EE}}[1]$
, and there exists a collection of elements
${\mathrm {EE}}[1]$
, and there exists a collection of elements
![]() $(c_n)_{n\in \mathbb {N}}$
of G such that the following holds.
$(c_n)_{n\in \mathbb {N}}$
of G such that the following holds.
-
(1) For any n, the equation
 $c_1=c_n^x$
has a unique solution, say
$c_1=c_n^x$
has a unique solution, say
 $k_n$
; this solution is positive.
$k_n$
; this solution is positive. -
(2) There is no primitive recursive function f such that
 $k_n\leqslant f(\max \{|c_n|_X,|c_1|_X\})$
.
$k_n\leqslant f(\max \{|c_n|_X,|c_1|_X\})$
.
Proof We enumerate all primitive recursive functions
![]() $g_1,g_2,\dots $
and, for any
$g_1,g_2,\dots $
and, for any
![]() $n\in ~\mathbb {N}$
, we define a function
$n\in ~\mathbb {N}$
, we define a function
![]() $f_n:\mathbb {N}\rightarrow \mathbb {N}$
by the rule
$f_n:\mathbb {N}\rightarrow \mathbb {N}$
by the rule
 $$ \begin{align*} f_n(x)=\overset{n}{\underset{i=1}{\sum}} \overset{x}{\underset{j=1}{\sum}}\, \, g_i(j),\hspace{2mm} x\in \mathbb{N}. \end{align*} $$
$$ \begin{align*} f_n(x)=\overset{n}{\underset{i=1}{\sum}} \overset{x}{\underset{j=1}{\sum}}\, \, g_i(j),\hspace{2mm} x\in \mathbb{N}. \end{align*} $$
Clearly,
![]() $f_n$
is primitive recursive, nondecreasing,
$f_n$
is primitive recursive, nondecreasing,
![]() $g_n\leqslant f_n$
, and
$g_n\leqslant f_n$
, and
![]() $f_n\leqslant f_{n+1}$
. Finally, we define a function
$f_n\leqslant f_{n+1}$
. Finally, we define a function
![]() $F:\mathbb {N}\rightarrow \mathbb {N}$
by the rule
$F:\mathbb {N}\rightarrow \mathbb {N}$
by the rule
Clearly, F is recursive. We also define rational numbers
![]() $c_1=1$
and
$c_1=1$
and
![]() $c_n=\frac {1}{F(n)}$
for
$c_n=\frac {1}{F(n)}$
for
![]() $n\geqslant 2$
. Then we fix a recursive presentation (written multiplicatively) for the group
$n\geqslant 2$
. Then we fix a recursive presentation (written multiplicatively) for the group
![]() $( \mathbb {Q}, + )$
:
$( \mathbb {Q}, + )$
:
where
![]() $\mathcal {C}_{\mathbb {Q}}$
is the Cayley table for
$\mathcal {C}_{\mathbb {Q}}$
is the Cayley table for
![]() $\mathbb {Q}$
. Note that
$\mathbb {Q}$
. Note that
![]() $c_1,c_2,\dots $
appear in this presentation and the equalities
$c_1,c_2,\dots $
appear in this presentation and the equalities
![]() $c_n^{F(n)}=c_1 (n,m\in \mathbb {N})$
follow from
$c_n^{F(n)}=c_1 (n,m\in \mathbb {N})$
follow from
![]() $\mathcal {C}_{\mathbb {Q}}$
. We may assume that they are in
$\mathcal {C}_{\mathbb {Q}}$
. We may assume that they are in
![]() $\mathcal {C}_{\mathbb {Q}}$
. It is clear that
$\mathcal {C}_{\mathbb {Q}}$
. It is clear that
![]() ${\mathrm {EE}}[1]$
is decidable for this presentation. By the choice of
${\mathrm {EE}}[1]$
is decidable for this presentation. By the choice of
![]() $F(n)$
, the elements
$F(n)$
, the elements
![]() $c_1,c_2,\dots $
generate
$c_1,c_2,\dots $
generate
![]() $\mathbb {Q}$
. By some obvious transformations, we obtain a recursive presentation of
$\mathbb {Q}$
. By some obvious transformations, we obtain a recursive presentation of
![]() $\mathbb {Q}$
in the form
$\mathbb {Q}$
in the form
so that
![]() ${\mathrm {EE}}[1]$
is decidable. We embed
${\mathrm {EE}}[1]$
is decidable. We embed
![]() $\mathbb {Q}$
into a finitely presented group
$\mathbb {Q}$
into a finitely presented group
![]() $G_3$
by the Ol’shanskii–Sapir construction, which we described in Steps 1–4 in Section 3. Note that since
$G_3$
by the Ol’shanskii–Sapir construction, which we described in Steps 1–4 in Section 3. Note that since
![]() $\mathbb {Q}$
has decidable conjugacy problem, we do not need to do Step 1. Thus, we start with Step 2, where we use the following map.
$\mathbb {Q}$
has decidable conjugacy problem, we do not need to do Step 1. Thus, we start with Step 2, where we use the following map.
-
• Let
 $\varphi _2$
map each
$\varphi _2$
map each
 $c_i$
to the word
$c_i$
to the word
 $a^{100}b^i a^{101}b^i\ldots a^{199}b^i$
(of length
$a^{100}b^i a^{101}b^i\ldots a^{199}b^i$
(of length
 $100i + 14950$
),
$100i + 14950$
),
 $i \in \mathbb {N}$
.
$i \in \mathbb {N}$
.
By Step 2,
![]() $\varphi _2$
extends to an embedding
$\varphi _2$
extends to an embedding
![]() $\varphi _2:\mathbb {Q}\rightarrow G_2$
, where the group
$\varphi _2:\mathbb {Q}\rightarrow G_2$
, where the group
![]() $G_2=\langle a,b\,|\, R_2\rangle $
is 2-generated, recursively presented, and has solvable power and conjugacy problems. Then we only apply Step 3. By this step, the map
$G_2=\langle a,b\,|\, R_2\rangle $
is 2-generated, recursively presented, and has solvable power and conjugacy problems. Then we only apply Step 3. By this step, the map
![]() $a\mapsto a$
,
$a\mapsto a$
,
![]() $b\mapsto b$
extends to an embedding
$b\mapsto b$
extends to an embedding
![]() $\varphi _3:G_2\rightarrow G_3$
, where
$\varphi _3:G_2\rightarrow G_3$
, where
![]() $G_3=\langle X|\, R_3\rangle $
is a finite presentation with solvable power and conjugacy problems, and
$G_3=\langle X|\, R_3\rangle $
is a finite presentation with solvable power and conjugacy problems, and
![]() $\{a,b\}\subseteq X$
. We set
$\{a,b\}\subseteq X$
. We set
![]() $G=G_3$
.
$G=G_3$
.
The statement (1) is valid: for any n, the equation
![]() $c_n^x=c_1$
has a unique solution, namely
$c_n^x=c_1$
has a unique solution, namely
![]() $k_n=F(n)$
. To prove statement (2), we first observe that
$k_n=F(n)$
. To prove statement (2), we first observe that
Suppose that statement (2) is not valid, i.e., there exists a primitive recursive function
![]() $g_m$
such that
$g_m$
such that
for any n. Using that
![]() $g_m\leqslant f_m$
and that
$g_m\leqslant f_m$
and that
![]() $f_m$
is nondecreasing, we deduce from (4.1) and (4.2) that
$f_m$
is nondecreasing, we deduce from (4.1) and (4.2) that
for any n. In particular,
![]() $F(m)\leqslant f_m(100m+14950)$
. This contradicts the definition of F.
$F(m)\leqslant f_m(100m+14950)$
. This contradicts the definition of F.
Remark 4.6 Theorem 4.2 in [Reference Lohrey and Zetzsche13] states that the KP in the Baumslag–Solitar group
![]() $\mathrm {BS}(1,2)$
is NP-computable, but the
$\mathrm {BS}(1,2)$
is NP-computable, but the
![]() ${\mathrm {EE}}[3]$
-estimation function for this group cannot be essentially smaller than the doubly exponential function. This statement can be considered as a counterpart of Proposition 4.5 at the level of polynomial computability.
${\mathrm {EE}}[3]$
-estimation function for this group cannot be essentially smaller than the doubly exponential function. This statement can be considered as a counterpart of Proposition 4.5 at the level of polynomial computability.
Remark 4.7 However, for hyperbolic groups,
![]() ${\mathrm {EE}}[n]$
-estimating functions can be chosen to be linear for any n (a polynomial estimation was known earlier; see [Reference Myasnikov, Nikolaev and Ushakov17]). This follows from the preprint [Reference Bier and Bogopolski1] of the first-named author and Bier. It is proved in [Reference Bier and Bogopolski1] that similar linearity result holds for acylindrically hyperbolic groups in the case of loxodromic coefficients
${\mathrm {EE}}[n]$
-estimating functions can be chosen to be linear for any n (a polynomial estimation was known earlier; see [Reference Myasnikov, Nikolaev and Ushakov17]). This follows from the preprint [Reference Bier and Bogopolski1] of the first-named author and Bier. It is proved in [Reference Bier and Bogopolski1] that similar linearity result holds for acylindrically hyperbolic groups in the case of loxodromic coefficients
![]() $g_i$
.
$g_i$
.
5 Restricted versions of
 ${\mathrm {EE}} [n]$
${\mathrm {EE}} [n]$
We introduce two new algorithmic problems which can be considered as fragments of
![]() ${\mathrm {EE}}[n]$
. Informally we call them the left and the right fragments of
${\mathrm {EE}}[n]$
. Informally we call them the left and the right fragments of
![]() ${\mathrm {EE}}[n]$
. We show that these fragments can take diverse computational complexities for the same finitely presented group (see Theorem B).
${\mathrm {EE}}[n]$
. We show that these fragments can take diverse computational complexities for the same finitely presented group (see Theorem B).
5.1 Definitions and observations
Below, we assume that G is given by a recursive presentation and X is the corresponding set of generators.
Definition 5.1 (1) Let
![]() $g_1 , \ldots , g_n \in G$
. By
$g_1 , \ldots , g_n \in G$
. By
![]() ${\mathrm {EE}} [G, g_1 , \ldots , g_n ]$
, we denote the set of all
${\mathrm {EE}} [G, g_1 , \ldots , g_n ]$
, we denote the set of all
![]() $g \in G$
such that the equation
$g \in G$
such that the equation
![]() $g = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
has a solution which is a tuple of integers. (2) For a fixed
$g = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
has a solution which is a tuple of integers. (2) For a fixed
![]() $g\in G$
, let
$g\in G$
, let
![]() ${\mathrm {EE}} [g,G^n]$
be the set consisting of all tuples
${\mathrm {EE}} [g,G^n]$
be the set consisting of all tuples
![]() $(g_1 ,\ldots ,g_n ) \in G^n$
such that the equation
$(g_1 ,\ldots ,g_n ) \in G^n$
such that the equation
![]() $g = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
has a solution which is a tuple of integers.
$g = g^{z_1}_{1} \cdot \cdots \cdot g^{z_n}_n$
has a solution which is a tuple of integers.
Note that for a tuple of units
![]() $\bar {1}$
, the membership problem for
$\bar {1}$
, the membership problem for
![]() ${\mathrm {EE}} [G, \bar {1}]$
is equivalent to the word problem. Decidability of the problem
${\mathrm {EE}} [G, \bar {1}]$
is equivalent to the word problem. Decidability of the problem
![]() ${\mathrm {EE}}[n]$
is a uniform form of decidability of all
${\mathrm {EE}}[n]$
is a uniform form of decidability of all
![]() ${\mathrm {EE}} [G, \bar {g}]$
(resp.
${\mathrm {EE}} [G, \bar {g}]$
(resp.
![]() ${\mathrm {EE}} [g,G^n]$
). Indeed, if for each
${\mathrm {EE}} [g,G^n]$
). Indeed, if for each
![]() $g\in G$
there is an algorithm (provided by the word g in an effective way) which decides the membership problem for
$g\in G$
there is an algorithm (provided by the word g in an effective way) which decides the membership problem for
![]() ${\mathrm {EE}} [g,G^n]$
, then
${\mathrm {EE}} [g,G^n]$
, then
![]() ${\mathrm {EE}}[n]$
is decidable. The similar statement holds for problems
${\mathrm {EE}}[n]$
is decidable. The similar statement holds for problems
![]() ${\mathrm {EE}} [G, g_1 , \ldots , g_n ]$
.
${\mathrm {EE}} [G, g_1 , \ldots , g_n ]$
.
Remark 5.2 Suppose that G is a group given by a recursive presentation. Let g be a nontrivial element of G. Suppose that
![]() ${\mathrm {EE}} [G, g]$
is decidable in G and the order of g is known. Then
${\mathrm {EE}} [G, g]$
is decidable in G and the order of g is known. Then
![]() $\mathrm {WP}$
is decidable in G.
$\mathrm {WP}$
is decidable in G.
Indeed, in order to determine whether a given h is trivial in G, we first verify whether h is a power of g. If h is not a power of g, then
![]() $h\not = 1$
. If h is a power of g, we start a diagonal computation for verification of the following equalities:
$h\not = 1$
. If h is a power of g, we start a diagonal computation for verification of the following equalities:
![]() $h=1$
,
$h=1$
,
![]() $h=g$
,
$h=g$
,
![]() $\ldots , h=g^k, \ldots $
. Here, we use the recursive presentation of G. At some stage, we will find a number k with
$\ldots , h=g^k, \ldots $
. Here, we use the recursive presentation of G. At some stage, we will find a number k with
![]() $h = g^k$
. Since the order of g is known, we can check whether
$h = g^k$
. Since the order of g is known, we can check whether
![]() $h=1$
or not.
$h=1$
or not.
Given a group G and a natural number
![]() $n\geqslant 1$
, how diverse can be algorithmic complexities of the problems
$n\geqslant 1$
, how diverse can be algorithmic complexities of the problems
![]() ${\mathrm {EE}}[g,G^n]$
, and
${\mathrm {EE}}[g,G^n]$
, and
![]() ${\mathrm {EE}}[G,g_1,\dots ,g_n]$
, where
${\mathrm {EE}}[G,g_1,\dots ,g_n]$
, where
![]() $g,g_1,\dots ,g_n$
run over G? How these complexities are related to the complexity of the problem
$g,g_1,\dots ,g_n$
run over G? How these complexities are related to the complexity of the problem
![]() ${\mathrm {EE}}[n]$
?
${\mathrm {EE}}[n]$
?
A partial answer to these problems (in the case where G is finitely presented) is given in Theorem B.
5.2 Example
Let
![]() $p_n$
denote the nth prime number. For any function
$p_n$
denote the nth prime number. For any function
![]() $F:\mathbb {N}\rightarrow \mathbb {N}^2$
and any
$F:\mathbb {N}\rightarrow \mathbb {N}^2$
and any
![]() $n\in \mathbb {N}$
, we denote
$n\in \mathbb {N}$
, we denote
![]() $(\mathrm {im} F)_n = \{ m\in \mathbb {N}\, |\, (n ,m)\in \mathrm {im} (F)\}$
and write
$(\mathrm {im} F)_n = \{ m\in \mathbb {N}\, |\, (n ,m)\in \mathrm {im} (F)\}$
and write
![]() $F=(F_1,F_2)$
.
$F=(F_1,F_2)$
.
Let
![]() $F:\mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function such that, for any
$F:\mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function such that, for any
![]() $n\in \mathbb {N}$
, we have either
$n\in \mathbb {N}$
, we have either
![]() $(\mathrm {im} F)_n = \emptyset $
or
$(\mathrm {im} F)_n = \emptyset $
or
Thus, all sets
![]() $(\mathrm {im} F)_n$
,
$(\mathrm {im} F)_n$
,
![]() $n\in \mathbb {N}$
, are pairwise disjoint. We put
$n\in \mathbb {N}$
, are pairwise disjoint. We put
and consider the group with the following recursive presentation:
where
 $$ \begin{align*} \mathcal{R}_1 & =\{[a_n,b_m]=1\,|\, n,m\in \mathbb{N},\,\, m=p_n^k\hspace{2mm} {\mathrm{for some}}\hspace{2mm} k\in \mathbb{N}\ \backslash \{0\}\},\\ \mathcal{R}_2 &=\{a_{F_1(n)}=b^n_{F_2(n)}\,|\, n\in \mathbb{N}\}. \end{align*} $$
$$ \begin{align*} \mathcal{R}_1 & =\{[a_n,b_m]=1\,|\, n,m\in \mathbb{N},\,\, m=p_n^k\hspace{2mm} {\mathrm{for some}}\hspace{2mm} k\in \mathbb{N}\ \backslash \{0\}\},\\ \mathcal{R}_2 &=\{a_{F_1(n)}=b^n_{F_2(n)}\,|\, n\in \mathbb{N}\}. \end{align*} $$
Theorem 5.3 For the above defined group G, the following statements are valid.
-
(1)
 $\mathrm {CP}(G)$
,
$\mathrm {CP}(G)$
,
 ${\mathrm {EE}}[1,G]$
, and
${\mathrm {EE}}[1,G]$
, and
 ${\mathrm {EE}}[G,1]$
are decidable.
${\mathrm {EE}}[G,1]$
are decidable. -
(2)
 ${\mathrm {EE}}[1]$
is undecidable for G if the set
${\mathrm {EE}}[1]$
is undecidable for G if the set
 $\mathrm {im}\, (F_1 )$
is not computable.
$\mathrm {im}\, (F_1 )$
is not computable. -
(3) For any fixed
 $g_0\in G$
, the problem
$g_0\in G$
, the problem
 ${\mathrm {EE}} [g_0 ,G]$
(resp.
${\mathrm {EE}} [g_0 ,G]$
(resp.
 ${\mathrm {EE}} [G,g_0 ]$
) is decidable or there is a number n such that
${\mathrm {EE}} [G,g_0 ]$
) is decidable or there is a number n such that
 ${\mathrm {EE}} [g_0 ,G]$
(resp.
${\mathrm {EE}} [g_0 ,G]$
(resp.
 ${\mathrm {EE}} [G,g_0 ]$
) is Turing reducible to
${\mathrm {EE}} [G,g_0 ]$
) is Turing reducible to
 $(\mathrm {im}\, F)_n$
. Each of these possibilities can be effectively recognized, and the corresponding number n can be computed.
$(\mathrm {im}\, F)_n$
. Each of these possibilities can be effectively recognized, and the corresponding number n can be computed. -
(4) If
 $n\in \mathrm {im}\, F_1$
, then the problem
$n\in \mathrm {im}\, F_1$
, then the problem
 ${\mathrm {EE}}[a_{n},G ]$
is computably equivalent to the membership problem for
${\mathrm {EE}}[a_{n},G ]$
is computably equivalent to the membership problem for
 $(\mathrm {im} F)_{n}$
.
$(\mathrm {im} F)_{n}$
.
Proof Before we start to prove these statements, we establish the structure of G. We decompose
![]() $X=\underset {i\in \mathbb {N}}\cup X_i$
, where
$X=\underset {i\in \mathbb {N}}\cup X_i$
, where
Let
![]() $H_i$
be the subgroup of G generated by
$H_i$
be the subgroup of G generated by
![]() $X_i$
. Then
$X_i$
. Then
To describe the structure of
![]() $H_i$
, we first introduce the following subgroups of
$H_i$
, we first introduce the following subgroups of
![]() $H_i$
:
$H_i$
:
Then
![]() $H_i^{-}$
is the free product of all its subgroups
$H_i^{-}$
is the free product of all its subgroups
![]() $\langle b_j\rangle $
, and
$\langle b_j\rangle $
, and
![]() $H_i^{+}$
is the amalgamated product over
$H_i^{+}$
is the amalgamated product over
![]() $\langle a_i\rangle $
of all its subgroups
$\langle a_i\rangle $
of all its subgroups
![]() $\langle b_j\rangle $
. Moreover, we have
$\langle b_j\rangle $
. Moreover, we have
Note that
![]() $\langle a_i\rangle $
is the center of
$\langle a_i\rangle $
is the center of
![]() $H_i$
.
$H_i$
.
Before we start the proof of statement (1), we make the following important observation.
Observation. Let
![]() $a_i ,b_j\in X$
and
$a_i ,b_j\in X$
and
![]() $k\in \mathbb {Z}\ \backslash \{ 0\}$
. Then
$k\in \mathbb {Z}\ \backslash \{ 0\}$
. Then
![]() $b_j^{k}$
is a power of
$b_j^{k}$
is a power of
![]() $a_i$
if and only if j is a power of
$a_i$
if and only if j is a power of
![]() $p_i$
and there exists a positive divisor d of k such that
$p_i$
and there exists a positive divisor d of k such that
![]() $F(d)=(i,j)$
. We can recognize the existence of such d since F is computable. If such d exists, then
$F(d)=(i,j)$
. We can recognize the existence of such d since F is computable. If such d exists, then
![]() $a_i=b_j^d$
and hence
$a_i=b_j^d$
and hence
![]() $a_i^{k/d}=b_j^k$
.
$a_i^{k/d}=b_j^k$
.
Proof of statement (1)
First, we prove that
![]() $\mathrm {WP}(G)$
is decidable. Using the normal form of an element of the free product (5.2), we reduce this problem to the following one. Given
$\mathrm {WP}(G)$
is decidable. Using the normal form of an element of the free product (5.2), we reduce this problem to the following one. Given
![]() $i\in \mathbb {N}$
and given a cyclically reduced nonempty word
$i\in \mathbb {N}$
and given a cyclically reduced nonempty word
![]() $a^s_i w(\bar {b})$
, where
$a^s_i w(\bar {b})$
, where
![]() $w(\bar {b})$
is over
$w(\bar {b})$
is over
![]() $X_i \ \backslash \{ a_i \}$
, decide whether the corresponding element of
$X_i \ \backslash \{ a_i \}$
, decide whether the corresponding element of
![]() $H_i$
is trivial or not.
$H_i$
is trivial or not.
We may assume that the word
![]() $w(\bar {b})$
is nonempty. Indeed, otherwise
$w(\bar {b})$
is nonempty. Indeed, otherwise
![]() $a^s_i w(\bar {b})$
lies in the cyclic subgroup
$a^s_i w(\bar {b})$
lies in the cyclic subgroup
![]() $\langle a_i \rangle $
of
$\langle a_i \rangle $
of
![]() $H_i$
and therefore is trivial exactly when
$H_i$
and therefore is trivial exactly when
![]() $s=0$
.
$s=0$
.
Using the above observation, we verify whether some subword
![]() $b_j^k$
of
$b_j^k$
of
![]() $w(\bar {b})$
is a power of
$w(\bar {b})$
is a power of
![]() $a_i$
or not. If no one such subword is a power of
$a_i$
or not. If no one such subword is a power of
![]() $a_i$
, then the element
$a_i$
, then the element
![]() $a^s_i w(\bar {b})$
is nontrivial in the amalgamated product (5.3). Suppose that some subword
$a^s_i w(\bar {b})$
is nontrivial in the amalgamated product (5.3). Suppose that some subword
![]() $b_j^k$
of
$b_j^k$
of
![]() $w(\bar {b})$
is a power of
$w(\bar {b})$
is a power of
![]() $a_i$
, say
$a_i$
, say
![]() $a_i^{\ell }=b_j^k$
. Since
$a_i^{\ell }=b_j^k$
. Since
![]() $a_i$
lies in the center of
$a_i$
lies in the center of
![]() $H_i$
, we can move this subword to the left and adjoin to
$H_i$
, we can move this subword to the left and adjoin to
![]() $a^s$
. After this operation,
$a^s$
. After this operation,
![]() $|w(\bar {b})|_{X_i \ \backslash \{ a_i \}}$
decreases and we can proceed by induction.
$|w(\bar {b})|_{X_i \ \backslash \{ a_i \}}$
decreases and we can proceed by induction.
Now, we show that the conjugacy problem in G is decidable. Using (5.2), we reduce this problem to the conjugacy problem in the groups
![]() $H_i$
,
$H_i$
,
![]() $i\in \mathbb {N}$
. By (5.3), each
$i\in \mathbb {N}$
. By (5.3), each
![]() $H_i$
is an amalgamated product over the center of
$H_i$
is an amalgamated product over the center of
![]() $H_i$
. This fact, the decidability of
$H_i$
. This fact, the decidability of
![]() $\mathrm {WP}(G)$
, and a criterion for conjugacy of elements in amalgamated products (see [Reference Lyndon and Schupp14, Chapter IV, Theorem 2.8]), imply that there is a universal algorithm deciding the conjugacy problem in each
$\mathrm {WP}(G)$
, and a criterion for conjugacy of elements in amalgamated products (see [Reference Lyndon and Schupp14, Chapter IV, Theorem 2.8]), imply that there is a universal algorithm deciding the conjugacy problem in each
![]() $H_i$
and hence in G.
$H_i$
and hence in G.
Decidability of
![]() ${\mathrm {EE}}[G,1]$
follows from decidability of the word problem, and for decidability of
${\mathrm {EE}}[G,1]$
follows from decidability of the word problem, and for decidability of
![]() ${\mathrm {EE}}[1,G]$
, observe that G is torsion-free.
${\mathrm {EE}}[1,G]$
, observe that G is torsion-free.
Proof of statement (2)
This statement easily follows from the equivalence
Indeed, if
![]() $\mathrm {im} F_1$
is not computable, we cannot decide, given
$\mathrm {im} F_1$
is not computable, we cannot decide, given
![]() $n\in \mathbb {N}$
, whether the equation
$n\in \mathbb {N}$
, whether the equation
![]() $a_n=b_{p_n}^x$
has a solution or not.
$a_n=b_{p_n}^x$
has a solution or not.
Proof of statement (3)
For a fixed element
![]() $g_0\in G$
, we study the problem
$g_0\in G$
, we study the problem
![]() ${\mathrm {EE}} [g_0 ,G]$
. Given another element
${\mathrm {EE}} [g_0 ,G]$
. Given another element
![]() $g_1\in G$
, we shall consider the exponential equation
$g_1\in G$
, we shall consider the exponential equation
We may assume that
![]() $g_0\neq 1$
; otherwise,
$g_0\neq 1$
; otherwise,
![]() ${\mathrm {EE}}[g_0,G]$
is decidable since G is torsion-free and
${\mathrm {EE}}[g_0,G]$
is decidable since G is torsion-free and
![]() $\mathrm {WP}(G)$
is decidable. Having
$\mathrm {WP}(G)$
is decidable. Having
![]() $g_0\neq 1$
, we may assume that
$g_0\neq 1$
, we may assume that
![]() $g_1\neq 1$
. Standardly, we assume that
$g_1\neq 1$
. Standardly, we assume that
![]() $g_0$
and
$g_0$
and
![]() $g_1$
are represented by some words u and v in the alphabet
$g_1$
are represented by some words u and v in the alphabet
![]() ${X=\underset {i\in \mathbb {N}}{\cup } X_i}$
. Thus, we consider the following exponential equation in G:
${X=\underset {i\in \mathbb {N}}{\cup } X_i}$
. Thus, we consider the following exponential equation in G:
We write
![]() $v=v_1v_2\dots v_{\ell }$
, where
$v=v_1v_2\dots v_{\ell }$
, where
![]() $v_i$
is a word in the alphabet
$v_i$
is a word in the alphabet
![]() $X_{\lambda (i)}$
for some
$X_{\lambda (i)}$
for some
![]() $\lambda (i)$
,
$\lambda (i)$
,
![]() $i=1,\dots ,\ell $
, and
$i=1,\dots ,\ell $
, and
![]() $\lambda (j)\neq \lambda (j+1)$
for
$\lambda (j)\neq \lambda (j+1)$
for
![]() $j=1,\dots ,\ell -1$
. Moreover, we assume that each
$j=1,\dots ,\ell -1$
. Moreover, we assume that each
![]() $v_i$
represents a nontrivial element of
$v_i$
represents a nontrivial element of
![]() $H_{\lambda (i)}$
. This can be recognized by decidability of
$H_{\lambda (i)}$
. This can be recognized by decidability of
![]() $\mathrm {WP}(G)$
. Using conjugation, we may additionally assume that
$\mathrm {WP}(G)$
. Using conjugation, we may additionally assume that
![]() $\lambda (1)\neq \lambda ( \ell )$
if
$\lambda (1)\neq \lambda ( \ell )$
if
![]() $\ell>1$
. Analogously, we write
$\ell>1$
. Analogously, we write
![]() $u=u_1u_2\dots u_{k}$
. Note that
$u=u_1u_2\dots u_{k}$
. Note that
![]() $v_1$
and
$v_1$
and
![]() $u_1$
(resp.
$u_1$
(resp.
![]() $v_{\ell }$
and
$v_{\ell }$
and
![]() $u_k$
) belong to the same subgroup
$u_k$
) belong to the same subgroup
![]() $H_j$
.
$H_j$
.
Suppose that
![]() $\ell>1$
. Then a necessary condition for solvability of equation (5.4) is
$\ell>1$
. Then a necessary condition for solvability of equation (5.4) is
![]() $k>1$
. If this condition is fulfilled, then any possible solution z of equation (5.4) satisfies
$k>1$
. If this condition is fulfilled, then any possible solution z of equation (5.4) satisfies
![]() $|z|=k/\ell $
, and the existence of a solution z can be verified using decidability of
$|z|=k/\ell $
, and the existence of a solution z can be verified using decidability of
![]() $\mathrm {WP}(G)$
.
$\mathrm {WP}(G)$
.
Note that until this moment the corresponding algorithm is uniform on u and v. In the following case, we will call some oracle depending on u.
Suppose that
![]() $\ell =1$
. Then
$\ell =1$
. Then
![]() $u\in H_n$
for
$u\in H_n$
for
![]() $n=\lambda (1)$
, and this n can be determined using the definition of
$n=\lambda (1)$
, and this n can be determined using the definition of
![]() $X_n$
. Using the procedure described in the proof of decidability of
$X_n$
. Using the procedure described in the proof of decidability of
![]() $\mathrm {WP}(G)$
, we write u in the normal form with respect to the amalgamated product (5.3), i.e., we write
$\mathrm {WP}(G)$
, we write u in the normal form with respect to the amalgamated product (5.3), i.e., we write
![]() $u = a^s_n b^{s_1}_{i_1} \ldots b^{s_r}_{i_r}$
where, in particular, each
$u = a^s_n b^{s_1}_{i_1} \ldots b^{s_r}_{i_r}$
where, in particular, each
![]() $b^{s_1}_{i_1}, \ldots , b^{s_r}_{i_r}$
does not have a subword which is a power of
$b^{s_1}_{i_1}, \ldots , b^{s_r}_{i_r}$
does not have a subword which is a power of
![]() $a_n$
. By using conjugation, we may additionally assume that u is cyclically reduced in the sense that
$a_n$
. By using conjugation, we may additionally assume that u is cyclically reduced in the sense that
![]() $i_1\neq i_r$
if
$i_1\neq i_r$
if
![]() $r>1$
.
$r>1$
.
Furthermore, we may now assume that v belongs to
![]() $H_{n}$
too. We also write v in the normal form with respect to the amalgamated product (5.3),
$H_{n}$
too. We also write v in the normal form with respect to the amalgamated product (5.3),
![]() $v = a^t_n b^{t_1}_{j_1} \ldots b^{t_q}_{j_q}$
.
$v = a^t_n b^{t_1}_{j_1} \ldots b^{t_q}_{j_q}$
.
If
![]() $r>1$
, then a necessary condition for solvability of equation (5.4) is
$r>1$
, then a necessary condition for solvability of equation (5.4) is
![]() $q>1$
. In this case, any possible solution z of (5.4) satisfies
$q>1$
. In this case, any possible solution z of (5.4) satisfies
![]() $|z|=r/q$
, and the existence of the corresponding z can be verified using decidability of
$|z|=r/q$
, and the existence of the corresponding z can be verified using decidability of
![]() $\mathrm {WP}(G)$
.
$\mathrm {WP}(G)$
.
Suppose that
![]() $r=1$
. Then a necessary condition for solvability of (5.4) is
$r=1$
. Then a necessary condition for solvability of (5.4) is
![]() $q =1$
and
$q =1$
and
![]() $i_1 = j_1$
. In this case, we only need to verify the existence of z satisfying (5.4) in the group
$i_1 = j_1$
. In this case, we only need to verify the existence of z satisfying (5.4) in the group
![]() $\langle a_n , b_{i_1} \rangle $
. This is the only place where we need the oracle for
$\langle a_n , b_{i_1} \rangle $
. This is the only place where we need the oracle for
![]() $(\mathrm {im} F)_n$
. Verifying whether
$(\mathrm {im} F)_n$
. Verifying whether
![]() $p_{n}\in (\mathrm {im} F)_{n}$
, we decide if
$p_{n}\in (\mathrm {im} F)_{n}$
, we decide if
![]() $n \in \mathrm {im} F_1$
. If this happens, we easily compute in the oracle
$n \in \mathrm {im} F_1$
. If this happens, we easily compute in the oracle
![]() $(\mathrm {im} F)_n$
the relation from the presentation (5.1) of the form
$(\mathrm {im} F)_n$
the relation from the presentation (5.1) of the form
![]() $a_{n} = b^m_{i_1}$
if it exists, and if it does not exist we recognize this. In the latter case, any possible solution z of equation (5.4) satisfies
$a_{n} = b^m_{i_1}$
if it exists, and if it does not exist we recognize this. In the latter case, any possible solution z of equation (5.4) satisfies
![]() $|z|\leqslant |u|_{X_n}$
. In the former case,
$|z|\leqslant |u|_{X_n}$
. In the former case,
![]() $\langle a_n , b_{i_1} \rangle = \langle b_{i_1} \rangle $
. Substituting
$\langle a_n , b_{i_1} \rangle = \langle b_{i_1} \rangle $
. Substituting
![]() $b^m_{i_1}$
instead of
$b^m_{i_1}$
instead of
![]() $a_n$
both in u and v, we obtain an equation in the cyclic group
$a_n$
both in u and v, we obtain an equation in the cyclic group
![]() $\langle b_{i_1} \rangle $
, and the number z can be computed. This gives an algorithm which is computable with respect to
$\langle b_{i_1} \rangle $
, and the number z can be computed. This gives an algorithm which is computable with respect to
![]() $(\mathrm {im}\, F)_n$
.
$(\mathrm {im}\, F)_n$
.
The case
![]() $r=0$
is trivial, and we leave it to the reader.
$r=0$
is trivial, and we leave it to the reader.
This completes the proof of statement (3) for
![]() ${\mathrm {EE}} [g_0 ,G]$
. The argument for
${\mathrm {EE}} [g_0 ,G]$
. The argument for
![]() ${\mathrm {EE}} [G,g_0 ]$
is analogous.
${\mathrm {EE}} [G,g_0 ]$
is analogous.
Proof of statement (4)
Let
![]() $n\in \mathrm {im}\, F_1$
. The following equivalence recognizes
$n\in \mathrm {im}\, F_1$
. The following equivalence recognizes
![]() $j \in (\mathrm {im}\, F)_n$
under the oracle for
$j \in (\mathrm {im}\, F)_n$
under the oracle for
![]() ${\mathrm {EE}} [a_n, G]$
:
${\mathrm {EE}} [a_n, G]$
:
Remark 5.4 Statements (1) and (4) also hold for the corresponding versions of the KP (where one looks for solutions in
![]() $\mathbb {N}$
).
$\mathbb {N}$
).
Theorem B There exists a finitely presented torsion-free group G with decidable conjugacy problem and undecidable
![]() ${\mathrm {EE}}[1]$
such that any r.e. Turing degree is realized as the Turing degree of the problem
${\mathrm {EE}}[1]$
such that any r.e. Turing degree is realized as the Turing degree of the problem
![]() ${\mathrm {EE}}[g,G]$
for appropriate
${\mathrm {EE}}[g,G]$
for appropriate
![]() $g\in G$
.
$g\in G$
.
Proof First, we construct a recursively presented group G with these properties. Let
![]() $\varphi (x,y)$
be Kleene’s universal computable function, i.e., it finds the output (if it exists) of the Turing machine with index x on input y. Let
$\varphi (x,y)$
be Kleene’s universal computable function, i.e., it finds the output (if it exists) of the Turing machine with index x on input y. Let
and let
![]() $\Phi : \mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function with
$\Phi : \mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function with
![]() $\mathrm {im}\, \Phi = W$
. Below, we use notations introduced at the beginning of this subsection. Obviously, the sets
$\mathrm {im}\, \Phi = W$
. Below, we use notations introduced at the beginning of this subsection. Obviously, the sets
![]() $(\mathrm {im}\, \Phi )_n$
,
$(\mathrm {im}\, \Phi )_n$
,
![]() $n\in \mathbb {N}$
, have all possible r.e. Turing degrees. Now, we extend the set W as follows:
$n\in \mathbb {N}$
, have all possible r.e. Turing degrees. Now, we extend the set W as follows:
Let
![]() $\widehat {\Phi }: \mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function with
$\widehat {\Phi }: \mathbb {N}\rightarrow \mathbb {N}^2$
be a total, injective, computable function with
![]() $\mathrm {im}\, \widehat {\Phi } = \widehat {W}$
. We have
$\mathrm {im}\, \widehat {\Phi } = \widehat {W}$
. We have
![]() $(\mathrm {im}\, \widehat {\Phi })_n=((\mathrm {im}\, \Phi )_n\ \backslash \{ 0 \})\cup \{1\}$
for nonempty
$(\mathrm {im}\, \widehat {\Phi })_n=((\mathrm {im}\, \Phi )_n\ \backslash \{ 0 \})\cup \{1\}$
for nonempty
![]() $(\mathrm {im}\, \Phi )_n$
and
$(\mathrm {im}\, \Phi )_n$
and
![]() $n\in \mathbb {N}$
. Therefore, the sets
$n\in \mathbb {N}$
. Therefore, the sets
![]() $(\mathrm {im}\, \widehat {\Phi })_n$
,
$(\mathrm {im}\, \widehat {\Phi })_n$
,
![]() $n\in \mathbb {N}$
, have all possible r.e. Turing degrees as well.
$n\in \mathbb {N}$
, have all possible r.e. Turing degrees as well.
Now, we define a function
![]() $F:\mathbb {N}\rightarrow \mathbb {N}^2$
by the formula
$F:\mathbb {N}\rightarrow \mathbb {N}^2$
by the formula
where
![]() $f:\mathbb {N}^2\rightarrow \mathbb {N}^2$
is the function sending each
$f:\mathbb {N}^2\rightarrow \mathbb {N}^2$
is the function sending each
![]() $(n,m)$
to
$(n,m)$
to
![]() $(n, p^m_n)$
. The function F satisfies the conditions formulated at the beginning of this subsection, since it is total, injective, computable, and for any
$(n, p^m_n)$
. The function F satisfies the conditions formulated at the beginning of this subsection, since it is total, injective, computable, and for any
![]() $n\in \mathbb {N}$
, we have either
$n\in \mathbb {N}$
, we have either
![]() $(\mathrm {im}\, \Phi )_n = \emptyset $
or
$(\mathrm {im}\, \Phi )_n = \emptyset $
or
Finally, we define a recursively presented group G by formula (5.1) and apply Theorem 5.3. By statements (1) and (2) of this theorem,
![]() $\mathrm {CP}(G)$
is decidable and
$\mathrm {CP}(G)$
is decidable and
![]() ${\mathrm {EE}}[1]$
is undecidable for G.
${\mathrm {EE}}[1]$
is undecidable for G.
The statement of Theorem B about Turing degrees follows from statement (4) of Theorem 5.3, which says that, for any
![]() $n\in \mathbb {N}$
, the problem
$n\in \mathbb {N}$
, the problem
![]() ${\mathrm {EE}}[a_{n},G ]$
is computably equivalent to the membership problem for
${\mathrm {EE}}[a_{n},G ]$
is computably equivalent to the membership problem for
![]() $(\mathrm {im}\, F)_{n}$
. It remains to note that
$(\mathrm {im}\, F)_{n}$
. It remains to note that
therefore, these sets have all possible r.e. Turing degrees.
In the second part of the proof, we embed the group G into a finitely presented group
![]() $\overline {G}$
using Ol’shanskii–Sapir construction explained in Remark 3.2. Note that we do not need to do Step 1 there since G already has solvable conjugacy problem, and we do not need to do Step 4 since we do not specially want
$\overline {G}$
using Ol’shanskii–Sapir construction explained in Remark 3.2. Note that we do not need to do Step 1 there since G already has solvable conjugacy problem, and we do not need to do Step 4 since we do not specially want
![]() $\overline {G}$
to be 2-generated.
$\overline {G}$
to be 2-generated.
Thus, using notations of this remark, we may assume that
![]() $G=G_1$
and that we have embeddings
$G=G_1$
and that we have embeddings
![]() $G_1\rightarrow G_2\rightarrow G_3$
, where
$G_1\rightarrow G_2\rightarrow G_3$
, where
![]() $G_3=\overline {G}$
. Simplifying notation, we assume
$G_3=\overline {G}$
. Simplifying notation, we assume
![]() $G_1\leqslant G_2\leqslant G_3$
. By this construction,
$G_1\leqslant G_2\leqslant G_3$
. By this construction,
![]() $G_3$
has solvable conjugacy problem if
$G_3$
has solvable conjugacy problem if
![]() $G_1$
has solvable conjugacy problem. The latter is valid, and hence
$G_1$
has solvable conjugacy problem. The latter is valid, and hence
![]() $\overline {G}$
has solvable conjugacy problem. It remains to prove the following claim.
$\overline {G}$
has solvable conjugacy problem. It remains to prove the following claim.
Claim For any
![]() $g\in G$
, the problems
$g\in G$
, the problems
![]() ${\mathrm {EE}}[g,G_1]$
and
${\mathrm {EE}}[g,G_1]$
and
![]() ${\mathrm {EE}}[g,G_3]$
are computationally equivalent.
${\mathrm {EE}}[g,G_3]$
are computationally equivalent.
Proof The computational equivalence of
![]() ${\mathrm {EE}}[g,G_1]$
and
${\mathrm {EE}}[g,G_1]$
and
![]() ${\mathrm {EE}}[g,G_2]$
follows from the proof of Lemma 11 in [Reference Ol’shanskii and Sapir20]. (We stress that we use the proof and not the formulation of this lemma which requires solvability of power problem in
${\mathrm {EE}}[g,G_2]$
follows from the proof of Lemma 11 in [Reference Ol’shanskii and Sapir20]. (We stress that we use the proof and not the formulation of this lemma which requires solvability of power problem in
![]() $G_1$
.) Indeed, given an exponential equation
$G_1$
.) Indeed, given an exponential equation
![]() $g=u^z$
with
$g=u^z$
with
![]() $u\in G_2$
, the proof (depending on u) either recursively reduces this equation to
$u\in G_2$
, the proof (depending on u) either recursively reduces this equation to
![]() ${\mathrm {EE}}[g,G_1]$
or gives a linear upper bound for
${\mathrm {EE}}[g,G_1]$
or gives a linear upper bound for
![]() $|z|$
in terms of g and u.
$|z|$
in terms of g and u.
The computational equivalence of
![]() ${\mathrm {EE}}[g,G_2]$
and
${\mathrm {EE}}[g,G_2]$
and
![]() ${\mathrm {EE}}[g,G_3]$
analogously follows from the proof of Lemma 12 in [Reference Ol’shanskii and Sapir20].
${\mathrm {EE}}[g,G_3]$
analogously follows from the proof of Lemma 12 in [Reference Ol’shanskii and Sapir20].
6 Complexity of the problem
 ${\mathrm {EE}}[n]$
${\mathrm {EE}}[n]$
Applying the approach of [Reference Bilanovic, Chubb and Roven2], we obtain the following proposition.
Proposition 6.1
-
(1) Detecting a group with decidable
 ${\mathrm {EE}} [n]$
is
${\mathrm {EE}} [n]$
is
 $\Sigma ^0_3$
in the class of recursively presented groups.
$\Sigma ^0_3$
in the class of recursively presented groups. -
(2) The same statement holds for the
 ${\mathrm {EE}}$
-problem and the KP.
${\mathrm {EE}}$
-problem and the KP.
Proof We will use standard terminology from [Reference Soare22]. Kleene’s universal computable function
![]() $\varphi (x,y)$
will be applied to several families of objects. As usual, these objects are coded by natural numbers.
$\varphi (x,y)$
will be applied to several families of objects. As usual, these objects are coded by natural numbers.
Take a computable indexation
![]() $G_i = \langle X \, | \, \mathcal {R}_i \rangle $
,
$G_i = \langle X \, | \, \mathcal {R}_i \rangle $
,
![]() $i\in \omega $
, of all recursively presented groups with respect to generators
$i\in \omega $
, of all recursively presented groups with respect to generators
![]() $X= \{ x_1, x_2 ,\ldots \}$
. Fix an algorithm which for the input
$X= \{ x_1, x_2 ,\ldots \}$
. Fix an algorithm which for the input
![]() $(i,s)$
outputs the sth equality of the form
$(i,s)$
outputs the sth equality of the form
![]() $w = 1$
satisfied in
$w = 1$
satisfied in
![]() $G_i$
. We see that the set of pairs
$G_i$
. We see that the set of pairs
![]() $(G_i ,w)$
, where
$(G_i ,w)$
, where
![]() $G_i \models (w=1)$
with
$G_i \models (w=1)$
with
![]() $w \in {\mathrm {F}}(X)$
, is computably enumerable. We use the notation
$w \in {\mathrm {F}}(X)$
, is computably enumerable. We use the notation
There exists a computable enumeration of the set of pair
![]() $(G_i ,\bar {w})$
where
$(G_i ,\bar {w})$
where
![]() $\bar {w} = (w_0 , w_1 , \ldots , w_n )$
belongs to
$\bar {w} = (w_0 , w_1 , \ldots , w_n )$
belongs to
![]() ${\mathrm {EE}} [n](G_i )$
. Thus, the set
${\mathrm {EE}} [n](G_i )$
. Thus, the set
is computably enumerable. These sets belong to
![]() $\Sigma ^0_1$
. On the other hand, the set
$\Sigma ^0_1$
. On the other hand, the set
belongs to
![]() $\Pi ^0_1$
. The property
$\Pi ^0_1$
. The property
![]() $(w_0 , w_1 , \ldots , w_n )\not \in {\mathrm {EE}}[n](G_i)$
exactly means that, for any
$(w_0 , w_1 , \ldots , w_n )\not \in {\mathrm {EE}}[n](G_i)$
exactly means that, for any
![]() $(s_0 , s_1 ,\ldots ,s_n )$
, the equality
$(s_0 , s_1 ,\ldots ,s_n )$
, the equality
![]() $w_0 = w^{s_1}_1 \cdot \cdots \cdot w^{s_n}_n$
is not recognized in
$w_0 = w^{s_1}_1 \cdot \cdots \cdot w^{s_n}_n$
is not recognized in
![]() $G_i$
at step
$G_i$
at step
![]() $|s_0|$
. Based on these observations, we formulate decidability of
$|s_0|$
. Based on these observations, we formulate decidability of
![]() ${\mathrm {EE}} [n]$
for
${\mathrm {EE}} [n]$
for
![]() $G_i$
as follows.
$G_i$
as follows.
There is a number
![]() $m\in \mathbb {N}$
such that, for any tuple
$m\in \mathbb {N}$
such that, for any tuple
![]() $w_0 , w_1 , \ldots , w_n\in {\mathrm {F}}(X)$
and any
$w_0 , w_1 , \ldots , w_n\in {\mathrm {F}}(X)$
and any
![]() $(s_0 , s_1 ,\ldots ,s_n )\in \mathbb {Z}^{n+1}$
, there exist numbers
$(s_0 , s_1 ,\ldots ,s_n )\in \mathbb {Z}^{n+1}$
, there exist numbers
![]() $\ell , k\in \mathbb {N}$
such that the following properties hold:
$\ell , k\in \mathbb {N}$
such that the following properties hold:
-
• The algorithm
 $\varphi (m,. )$
applied to the code of
$\varphi (m,. )$
applied to the code of
 $\bar {w}$
gives the value
$\bar {w}$
gives the value
 $0$
or
$0$
or
 $1$
at step
$1$
at step
 $\ell $
.
$\ell $
. -
• The algorithm
 $\varphi (m,. )$
applied to the code of
$\varphi (m,. )$
applied to the code of
 $\bar {w}$
gives the value
$\bar {w}$
gives the value
 $0$
at step
$0$
at step
 $\ell $
or the membership
$\ell $
or the membership
 $G_i \in I_{\bar {w}}$
is confirmed at step k of computation.
$G_i \in I_{\bar {w}}$
is confirmed at step k of computation. -
• The algorithm
 $\varphi (m,. )$
applied to the code of
$\varphi (m,. )$
applied to the code of
 $\bar {w}$
gives the value
$\bar {w}$
gives the value
 $1$
at step
$1$
at step
 $\ell $
or the equality
$\ell $
or the equality
 $w_0 = w^{s_1}_1 \cdot \cdots \cdot w^{s_n}_n$
is not recognized at step
$w_0 = w^{s_1}_1 \cdot \cdots \cdot w^{s_n}_n$
is not recognized at step
 $|s_0|$
.
$|s_0|$
.
The second statement of the proposition is similar.
Problem 3 Are
![]() ${\mathrm {EE}} [n]$
and the KP
${\mathrm {EE}} [n]$
and the KP
![]() $\Sigma ^0_3$
-complete in the class of recursively presented groups?
$\Sigma ^0_3$
-complete in the class of recursively presented groups?
Acknowledgment
The authors are grateful to the referee for very helpful remarks. In particular, the proof of Lemma 2.3 given in the paper belongs to the referee. It simplifies the original argument of the authors.