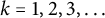1 Introduction
Benford’s law, named for physicist Frank Benford (though discovered almost 60 years prior by Simon Newcomb), refers to the observation that in many naturally occurring datasets, the leading digits are far from uniformly distributed, with smaller digits more likely to occur. Let us make this precise. By the N leading digits of the positive real number x, we mean the N most significant digits. For example (working in base
![]() $10$
),
$10$
),
![]() $123.456$
has the first
$123.456$
has the first
![]() $4$
leading digits
$4$
leading digits
![]() $1234$
, and this is the same for
$1234$
, and this is the same for
![]() $0.00123456$
. Now, let D and b be integers with
$0.00123456$
. Now, let D and b be integers with
![]() $b\ge 2$
. We say a positive real number “begins with D in base b” if its most significant digits in base b are those of the base b expansion of D. Then Benford’s law, in base b, predicts that the proportion of terms in the dataset beginning with D should be approximately
$b\ge 2$
. We say a positive real number “begins with D in base b” if its most significant digits in base b are those of the base b expansion of D. Then Benford’s law, in base b, predicts that the proportion of terms in the dataset beginning with D should be approximately
![]() $\log (1+D^{-1})/\log {b}$
. For example, since
$\log (1+D^{-1})/\log {b}$
. For example, since
![]() $\frac {\log {2}}{\log {10}}=0.3010\dots $
, we expect to see a leading digit
$\frac {\log {2}}{\log {10}}=0.3010\dots $
, we expect to see a leading digit
![]() $1$
in base 10 about
$1$
in base 10 about
![]() $30\%$
of the time.
$30\%$
of the time.
For general background on Benford’s law, see [Reference Berger and Hill5, Reference Miller22]. In this paper, we are interested in datasets arising from positive-valued arithmetic functions. Let
![]() $f\colon \mathbb {N} \to \mathbb {R}_{>0}$
. We say f obeys Benford’s law in base b (or that f is Benford in base b) if, for each positive integer D, the asymptotic density of n for which
$f\colon \mathbb {N} \to \mathbb {R}_{>0}$
. We say f obeys Benford’s law in base b (or that f is Benford in base b) if, for each positive integer D, the asymptotic density of n for which
![]() $f(n)$
begins with D in base b is
$f(n)$
begins with D in base b is
![]() $\log (1+D^{-1})/\log {b}$
. Results on the “Benfordity” of particular arithmetic functions are scattered throughout the literature. For example,
$\log (1+D^{-1})/\log {b}$
. Results on the “Benfordity” of particular arithmetic functions are scattered throughout the literature. For example,
![]() $f(n)=n!$
is Benford in every base b [Reference Diaconis11], as is the “primorial”
$f(n)=n!$
is Benford in every base b [Reference Diaconis11], as is the “primorial”
![]() $f(n) = \prod _{k=1}^{n}p_k$
[Reference Massé and Schneider21]. The classical partition function
$f(n) = \prod _{k=1}^{n}p_k$
[Reference Massé and Schneider21]. The classical partition function
![]() $p(n)$
is also Benford in every base (see [Reference Anderson, Rolen and Stoehr2] or [Reference Massé and Schneider21]). On the other hand,
$p(n)$
is also Benford in every base (see [Reference Anderson, Rolen and Stoehr2] or [Reference Massé and Schneider21]). On the other hand,
![]() $f(n)=n$
is not Benford; the asymptotic density in question does not exist. This same obstruction to Benford’s law persists if
$f(n)=n$
is not Benford; the asymptotic density in question does not exist. This same obstruction to Benford’s law persists if
![]() $f(n)$
is any positive-valued polynomial function of n. (See, for instance, the final section of [Reference Massé and Schneider21]. It should be noted that these examples obey Benford’s law in a weaker sense; namely, Benford’s law holds if asymptotic density is replaced with logarithmic density.)
$f(n)$
is any positive-valued polynomial function of n. (See, for instance, the final section of [Reference Massé and Schneider21]. It should be noted that these examples obey Benford’s law in a weaker sense; namely, Benford’s law holds if asymptotic density is replaced with logarithmic density.)
When f is multiplicative, whether or not f is Benford in base b can be interpreted as a problem in the theory of mean values of multiplicative functions. Namely, f is Benford precisely when
![]() $f(n)^{2\pi i \ell /\log {b}}$
has mean value zero for each nonzero integer
$f(n)^{2\pi i \ell /\log {b}}$
has mean value zero for each nonzero integer
![]() $\ell $
. This criterion was noted by Aursukaree and Chandee [Reference Aursukaree and Chandee3] and used by them to show that the divisor function
$\ell $
. This criterion was noted by Aursukaree and Chandee [Reference Aursukaree and Chandee3] and used by them to show that the divisor function
![]() $d(n)$
is Benford in base
$d(n)$
is Benford in base
![]() $10$
. A more systematic study of the Benford behavior of multiplicative functions, leveraging Halász’s celebrated mean value theorem, was recently undertaken in [Reference Chandee, Li, Pollack and Singha Roy8]. For example, it is shown there that
$10$
. A more systematic study of the Benford behavior of multiplicative functions, leveraging Halász’s celebrated mean value theorem, was recently undertaken in [Reference Chandee, Li, Pollack and Singha Roy8]. For example, it is shown there that
![]() $\phi (n)$
is not Benford, but that
$\phi (n)$
is not Benford, but that
![]() $|\tau (n)|$
is, where
$|\tau (n)|$
is, where
![]() $\tau $
is Ramanujan’s
$\tau $
is Ramanujan’s
![]() $\tau $
-function.Footnote
1
All of the work in [Reference Chandee, Li, Pollack and Singha Roy8] is carried out in base
$\tau $
-function.Footnote
1
All of the work in [Reference Chandee, Li, Pollack and Singha Roy8] is carried out in base
![]() $10$
, but both of the quoted results hold, by simple modifications of the proofs, in each fixed base
$10$
, but both of the quoted results hold, by simple modifications of the proofs, in each fixed base
![]() $b\ge 2$
.
$b\ge 2$
.
Our concern in the present paper is with certain nonmultiplicative functions. Roughly speaking, we show that (for each fixed k) the kth largest prime factor of n obeys Benford’s law, as does the sum of all of the prime factors of n. (Both results hold for each base b.) In fact, our results are somewhat stronger than this.
We let
![]() $P_k(n)$
denote the kth largest prime factor of n; when
$P_k(n)$
denote the kth largest prime factor of n; when
![]() $k=1$
, we write
$k=1$
, we write
![]() $P(n)$
in place of the more cumbersome
$P(n)$
in place of the more cumbersome
![]() $P_1(n)$
. More precisely, if
$P_1(n)$
. More precisely, if
![]() $n = p_1 p_2 p_3 \cdots p_{\Omega (n)}$
, with
$n = p_1 p_2 p_3 \cdots p_{\Omega (n)}$
, with
![]() $p_1 \ge p_2 \ge p_3 \ge \dots \ge p_{\Omega (n)}$
, we set
$p_1 \ge p_2 \ge p_3 \ge \dots \ge p_{\Omega (n)}$
, we set
![]() $P_k(n) = p_k$
, with the convention that
$P_k(n) = p_k$
, with the convention that
![]() $P_k(n) = 0$
if
$P_k(n) = 0$
if
![]() $k> \Omega (n)$
. Put
$k> \Omega (n)$
. Put
(When
![]() $k=1$
, it is usual to write
$k=1$
, it is usual to write
![]() $\Psi (x,y)$
in place of
$\Psi (x,y)$
in place of
![]() $\Psi _1(x,y)$
.) Let
$\Psi _1(x,y)$
.) Let
![]() $a\bmod {q}$
be a coprime residue class. For real
$a\bmod {q}$
be a coprime residue class. For real
![]() $x, y\ge 2$
, define
$x, y\ge 2$
, define
 $$\begin{align*}\begin{aligned} \Psi_k(x,y;b,D,q,a) := \#\{n \le x: P_k(n)\le y, ~P_k(n)\equiv a\ \ \ \pmod{q},\hphantom{extra}\\ P_k(n) \text{ begins with } D \text{ in base } b\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \Psi_k(x,y;b,D,q,a) := \#\{n \le x: P_k(n)\le y, ~P_k(n)\equiv a\ \ \ \pmod{q},\hphantom{extra}\\ P_k(n) \text{ begins with } D \text{ in base } b\}. \end{aligned} \end{align*}$$
Theorem 1.1 Fix positive integers k, b, and D, with
![]() $b\ge 2$
. Fix real numbers
$b\ge 2$
. Fix real numbers
![]() $U\ge 1$
and
$U\ge 1$
and
![]() $\epsilon>0$
. Then
$\epsilon>0$
. Then
 $$\begin{align*}\Psi_k(x,y;b,D,q,a) \sim \frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} \Psi_k(x,y),\end{align*}$$
$$\begin{align*}\Psi_k(x,y;b,D,q,a) \sim \frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} \Psi_k(x,y),\end{align*}$$
as
![]() $x, y \to \infty $
, uniformly for
$x, y \to \infty $
, uniformly for
![]() $y\ge x^{1/U}$
and coprime residue classes
$y\ge x^{1/U}$
and coprime residue classes
![]() $a\bmod {q}$
with
$a\bmod {q}$
with
![]() $q\le \frac {\log {x}}{(\log \log x)^{k-1+\epsilon }}$
. In fact, if
$q\le \frac {\log {x}}{(\log \log x)^{k-1+\epsilon }}$
. In fact, if
![]() $k=1$
, we can take
$k=1$
, we can take
![]() $q \le (\log {x})^{A}$
for any fixed A.
$q \le (\log {x})^{A}$
for any fixed A.
To deduce that
![]() $P_k(n)$
is Benford, it suffices to take
$P_k(n)$
is Benford, it suffices to take
![]() $q=1$
and
$q=1$
and
![]() $y=x$
. The additional generality of Theorem 1.1 seems of some interest. For example, Theorem 1.1 contains the result of Banks–Harman–Shparlinski [Reference Banks, Harman and Shparlinski4] that
$y=x$
. The additional generality of Theorem 1.1 seems of some interest. For example, Theorem 1.1 contains the result of Banks–Harman–Shparlinski [Reference Banks, Harman and Shparlinski4] that
![]() $P(n)$
, on integers
$P(n)$
, on integers
![]() $n\le x$
, is uniformly distributed in coprime residue classes mod q, for q up to an arbitrary fixed power of
$n\le x$
, is uniformly distributed in coprime residue classes mod q, for q up to an arbitrary fixed power of
![]() $\log {x}$
. Theorem 1.1 gives the corresponding result for
$\log {x}$
. Theorem 1.1 gives the corresponding result for
![]() $P_k(n)$
, when
$P_k(n)$
, when
![]() $k>1$
, in the more restricted range
$k>1$
, in the more restricted range
![]() $q \le {\log {x}}/{(\log \log x)^{k-1+\epsilon }}$
. This appears to be new; moreover, this range of q is sharp up to the power of
$q \le {\log {x}}/{(\log \log x)^{k-1+\epsilon }}$
. This appears to be new; moreover, this range of q is sharp up to the power of
![]() $\log \log {x}$
, since
$\log \log {x}$
, since
![]() $\gg x(\log \log {x})^{k-2}/\log {x}$
values of
$\gg x(\log \log {x})^{k-2}/\log {x}$
values of
![]() $n\le x$
have
$n\le x$
have
![]() $P_k(n)=2$
.
$P_k(n)=2$
.
Turning to the sum of the prime factors, we let
![]() $A(n)= \sum _{p^k\parallel n} kp$
. That is,
$A(n)= \sum _{p^k\parallel n} kp$
. That is,
![]() $A(n)$
is the sum of the prime factors of n, counting multiplicity. (The sum of the distinct prime factors of n could be handled by similar arguments.) The function
$A(n)$
is the sum of the prime factors of n, counting multiplicity. (The sum of the distinct prime factors of n could be handled by similar arguments.) The function
![]() $A(n)$
was introduced by Alladi and first investigated by Alladi and Erdős [Reference Alladi and Erdős1].
$A(n)$
was introduced by Alladi and first investigated by Alladi and Erdős [Reference Alladi and Erdős1].
Define
 $$\begin{align*}\begin{aligned} N(x,y; b, D, q, a) := \#\{n \le x: P(n)\le y, A(n)\equiv a\ \ \ \pmod{q},\hphantom{extra}\\ A(n) \text{ begins with } D \text{ in base } b\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} N(x,y; b, D, q, a) := \#\{n \le x: P(n)\le y, A(n)\equiv a\ \ \ \pmod{q},\hphantom{extra}\\ A(n) \text{ begins with } D \text{ in base } b\}. \end{aligned} \end{align*}$$
Theorem 1.2 Fix an integer
![]() $b \ge 2$
, and a positive integer D. Fix real numbers
$b \ge 2$
, and a positive integer D. Fix real numbers
![]() $U\ge 1$
and
$U\ge 1$
and
![]() $\epsilon>0$
. Then
$\epsilon>0$
. Then
 $$\begin{align*}N(x,y;b,D,q,a) \sim \frac 1q \frac{\log(1+D^{-1})}{\log{b}} \Psi(x,y),\end{align*}$$
$$\begin{align*}N(x,y;b,D,q,a) \sim \frac 1q \frac{\log(1+D^{-1})}{\log{b}} \Psi(x,y),\end{align*}$$
as
![]() $x, y \to \infty $
, uniformly for
$x, y \to \infty $
, uniformly for
![]() $y\ge x^{1/U}$
and residue classes
$y\ge x^{1/U}$
and residue classes
![]() $a\bmod {q}$
with
$a\bmod {q}$
with
![]() $q \le (\log {x})^{\frac {1}{2}-\epsilon }$
.
$q \le (\log {x})^{\frac {1}{2}-\epsilon }$
.
As before, taking
![]() $y=x$
and
$y=x$
and
![]() $q=1$
shows that
$q=1$
shows that
![]() $A(n)$
satisfies Benford’s law. Again, the extra generality here seems interesting. For example, it is implicit in Theorem 1.2 that
$A(n)$
satisfies Benford’s law. Again, the extra generality here seems interesting. For example, it is implicit in Theorem 1.2 that
![]() $A(n)$
is equidistributed mod q, uniformly for
$A(n)$
is equidistributed mod q, uniformly for
![]() $q \le (\log {x})^{\frac {1}{2}-\epsilon }$
, a result which we have not seen explicitly stated in the literature before. (See [Reference Goldfeld12] for the case of fixed q.) The same range of uniformity may follow from the method of Hall in [Reference Hall15] (who considered the distribution mod q of
$q \le (\log {x})^{\frac {1}{2}-\epsilon }$
, a result which we have not seen explicitly stated in the literature before. (See [Reference Goldfeld12] for the case of fixed q.) The same range of uniformity may follow from the method of Hall in [Reference Hall15] (who considered the distribution mod q of
![]() $\sum _{p\mid n,~p\nmid q} p$
), but our proof exhibits the result as a simple consequence of quantitative mean value theorems.
$\sum _{p\mid n,~p\nmid q} p$
), but our proof exhibits the result as a simple consequence of quantitative mean value theorems.
In addition to the already-mentioned references, the reader interested in number-theoretic investigations of Benford’s law might also consult [Reference Best, Dynes, Edelsbrunner, McDonald, Miller, Tor, Turnage-Butterbaugh and Weinstein6, Reference Best, Dynes, Edelsbrunner, McDonald, Miller, Tor, Turnage-Butterbaugh and Weinstein7, Reference Chen, Park and Swaminathan9, Reference Jameson, Thorner and Ye18, Reference Kontorovich and Miller20, Reference Pollack and Singha Roy24].
Notation
Most of our notation is standard. Of note, we allow constants in O-symbols to depend on any parameter that has been declared as “fixed.” When we refer to “large” x, the threshold for large enough may also depend on these parameters. We write
![]() $A\gtrsim B$
as an abbreviation for
$A\gtrsim B$
as an abbreviation for
![]() $A\ge (1+o(1))B$
.
$A\ge (1+o(1))B$
.
2 Benford’s law for
 $P_k(n)$
: proof of Theorem 1.1
$P_k(n)$
: proof of Theorem 1.1
We make crucial use of both the results and methods of Knuth and Trabb Pardo [Reference Knuth and Trabb Pardo19], who were the first to seriously investigate
![]() $P_k(n)$
when
$P_k(n)$
when
![]() $k>1$
. We define functions
$k>1$
. We define functions
![]() $\rho _k(\alpha )$
, for integers
$\rho _k(\alpha )$
, for integers
![]() $k\ge 0$
and real
$k\ge 0$
and real
![]() $\alpha $
, as follows:
$\alpha $
, as follows:
Much is known about the asymptotic behavior of
![]() $\rho _k(\alpha )$
as
$\rho _k(\alpha )$
as
![]() $\alpha \to \infty $
; for
$\alpha \to \infty $
; for
![]() $k=1$
, see, for instance, [Reference de Bruijn10], whereas for
$k=1$
, see, for instance, [Reference de Bruijn10], whereas for
![]() $k\ge 2$
, see equations (6.4) and (6.15) in [Reference Knuth and Trabb Pardo19]. For our purposes, much weaker information suffices. We assume as known that each
$k\ge 2$
, see equations (6.4) and (6.15) in [Reference Knuth and Trabb Pardo19]. For our purposes, much weaker information suffices. We assume as known that each
![]() $\rho _k$
(
$\rho _k$
(
![]() $k=1,2,3,\dots $
) is positive-valued and weakly decreasing on
$k=1,2,3,\dots $
) is positive-valued and weakly decreasing on
![]() $(0,\infty )$
, and that
$(0,\infty )$
, and that
![]() $\lim _{\alpha \to \infty } \rho _k(\alpha )=0$
.
$\lim _{\alpha \to \infty } \rho _k(\alpha )=0$
.
The following result, which connects the
![]() $\rho _k$
with the distribution of
$\rho _k$
with the distribution of
![]() $P_k(n)$
, appears as equation (4.7) in [Reference Knuth and Trabb Pardo19] (and is a consequence of the stronger assertion (4.8) shown there).
$P_k(n)$
, appears as equation (4.7) in [Reference Knuth and Trabb Pardo19] (and is a consequence of the stronger assertion (4.8) shown there).
Proposition 2.1 Fix a positive integer k and a real number
![]() $U\ge 1$
. For all
$U\ge 1$
. For all
![]() $x, y\ge 2$
,
$x, y\ge 2$
,
uniformly for
![]() $y\ge x^{1/U}$
, where
$y\ge x^{1/U}$
, where
![]() $u:=\frac {\log {x}}{\log {y}}$
. In particular,
$u:=\frac {\log {x}}{\log {y}}$
. In particular,
![]() $\Psi _k(x,y) \sim \rho _k(u) x$
as
$\Psi _k(x,y) \sim \rho _k(u) x$
as
![]() $x\to \infty $
, uniformly for
$x\to \infty $
, uniformly for
![]() $y\ge x^{1/U}$
.
$y\ge x^{1/U}$
.
(In [Reference Knuth and Trabb Pardo19], it is assumed that the ratio
![]() $\frac {\log {x}}{\log {y}}$
is fixed, rather than merely bounded. However, the proof given actually establishes (2.2) in the full range of Proposition 2.1.)
$\frac {\log {x}}{\log {y}}$
is fixed, rather than merely bounded. However, the proof given actually establishes (2.2) in the full range of Proposition 2.1.)
The next result is a variant of Theorem 1.1 where we require that
![]() $P_k(n)$
be bounded below by a fixed power of x.
$P_k(n)$
be bounded below by a fixed power of x.
Proposition 2.2 Fix positive integers k, b, and D with
![]() $b\ge 2$
. Fix real numbers
$b\ge 2$
. Fix real numbers
![]() $A\ge 1$
,
$A\ge 1$
,
![]() $U\ge 1$
, and fix a real number
$U\ge 1$
, and fix a real number
![]() $U'> U$
. The number of
$U'> U$
. The number of
![]() $n\le x$
for which
$n\le x$
for which
![]() $P_k(n)\equiv a\ \pmod {q}$
,
$P_k(n)\equiv a\ \pmod {q}$
,
![]() $P_k(n)$
begins with the digits of D in base b, and
$P_k(n)$
begins with the digits of D in base b, and
![]() $P_k(n) \in (x^{1/U'}, y]$
is
$P_k(n) \in (x^{1/U'}, y]$
is
 $$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')) x + o(x/\phi(q)), \end{align*}$$
$$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')) x + o(x/\phi(q)), \end{align*}$$
where
![]() $u:=\frac {\log {x}}{\log {y}}$
, where
$u:=\frac {\log {x}}{\log {y}}$
, where
![]() $x, y\to \infty $
with
$x, y\to \infty $
with
![]() $y\ge x^{1/U}$
, and where
$y\ge x^{1/U}$
, and where
![]() $a\bmod {q}$
is a coprime residue class with
$a\bmod {q}$
is a coprime residue class with
![]() $q \le (\log {x})^{A}$
.
$q \le (\log {x})^{A}$
.
The proof of Proposition 2.2 requires two classical results from the theory of primes in arithmetic progressions. Let
![]() $\pi (x;q,a)$
denote the count of primes
$\pi (x;q,a)$
denote the count of primes
![]() $p\le x$
with
$p\le x$
with
![]() $p\equiv a\ \pmod {q}$
.
$p\equiv a\ \pmod {q}$
.
Proposition 2.3 (Brun–Titchmarsh)
If a and q are coprime integers with
![]() $0 < 2q \le x$
, then
$0 < 2q \le x$
, then
Here, the implied constant is absolute.
Proposition 2.4 (Siegel–Walfisz)
Fix a real number
![]() $A> 0$
. If a and
$A> 0$
. If a and
![]() $ q$
are coprime integers with
$ q$
are coprime integers with
![]() $1 \le q \le (\log {x})^A$
, and
$1 \le q \le (\log {x})^A$
, and
![]() $x\ge 3$
, then
$x\ge 3$
, then
Here, C is a certain absolute constant.
For proofs of these results, see [Reference Montgomery and Vaughan23, Theorem 3.9, p. 90] and [Reference Montgomery and Vaughan23, Corollary 11.21, p. 382].
Proof of Proposition 2.2
First note that we can (and will) always assume that
![]() $y\le x$
, since the cases when
$y\le x$
, since the cases when
![]() $y> x$
are covered by the case
$y> x$
are covered by the case
![]() $y=x$
.
$y=x$
.
By a standard compactness argument, when proving Proposition 2.2, we may assume that
![]() $u= \frac {\log {x}}{\log {y}}$
is fixed. To see this, suppose Proposition 2.2 holds when u is fixed but does not hold in general. Then, for some
$u= \frac {\log {x}}{\log {y}}$
is fixed. To see this, suppose Proposition 2.2 holds when u is fixed but does not hold in general. Then, for some
![]() $\epsilon>0$
, there are choices of
$\epsilon>0$
, there are choices of
![]() $x, y, a$
, and q with x arbitrarily large,
$x, y, a$
, and q with x arbitrarily large,
![]() $x\ge y\ge x^{1/U}$
, and
$x\ge y\ge x^{1/U}$
, and
![]() $q\le (\log {x})^{A}$
for which our count exceeds
$q\le (\log {x})^{A}$
for which our count exceeds
 $$ \begin{align} \frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')+\epsilon) x, \end{align} $$
$$ \begin{align} \frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')+\epsilon) x, \end{align} $$
or there are such choices of
![]() $x,y,a$
, and q for which our count falls below
$x,y,a$
, and q for which our count falls below
 $$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')-\epsilon) x. \end{align*}$$
$$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(u)-\rho_k(U')-\epsilon) x. \end{align*}$$
We will assume that we are in the former case; the latter can be handled analogously. By compactness, we may choose
![]() $x,y,a,q$
so that
$x,y,a,q$
so that
![]() $u\to u_0$
, for some
$u\to u_0$
, for some
![]() $u_0 \in [1,U]$
.
$u_0 \in [1,U]$
.
We first rule out
![]() $u_0=1$
. As
$u_0=1$
. As
![]() $y\le x$
, the condition
$y\le x$
, the condition
![]() $P_k(n) \le y$
is always at least as strict as the condition
$P_k(n) \le y$
is always at least as strict as the condition
![]() $P_k(n) \le x$
(which holds vacuously, as we are counting numbers
$P_k(n) \le x$
(which holds vacuously, as we are counting numbers
![]() ${n\le x}$
). Moreover, the
${n\le x}$
). Moreover, the
![]() $u=1$
case of Proposition 2.2 is true by hypothesis. Putting these observations together, we see that the count of n corresponding to
$u=1$
case of Proposition 2.2 is true by hypothesis. Putting these observations together, we see that the count of n corresponding to
![]() $x,y,a,q$
is at most
$x,y,a,q$
is at most
 $$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(1)-\rho_k(U')+o(1)) x. \end{align*}$$
$$\begin{align*}\frac{1}{\phi(q)} \frac{\log(1+D^{-1})}{\log{b}} (\rho_k(1)-\rho_k(U')+o(1)) x. \end{align*}$$
However, if
![]() $u\to 1$
, then
$u\to 1$
, then
![]() $\rho _k(u)\to \rho _k(1)$
, and this estimate is eventually incompatible with (2.3).
$\rho _k(u)\to \rho _k(1)$
, and this estimate is eventually incompatible with (2.3).
Thus, it must be that
![]() $u_0> 1$
. Here, we may obtain a contradiction by a slightly tweaked argument. For any fixed
$u_0> 1$
. Here, we may obtain a contradiction by a slightly tweaked argument. For any fixed
![]() $\delta>0$
, we eventually have
$\delta>0$
, we eventually have
![]() $u> u_0-\delta $
. So the condition
$u> u_0-\delta $
. So the condition
![]() $P_k(n) \le y$
is eventually stricter than the condition
$P_k(n) \le y$
is eventually stricter than the condition
![]() $P_k(n) \le x^{1/(u_0-\delta )}$
. If
$P_k(n) \le x^{1/(u_0-\delta )}$
. If
![]() $\delta $
is fixed sufficiently small (in terms of
$\delta $
is fixed sufficiently small (in terms of
![]() $\epsilon $
), then the
$\epsilon $
), then the
![]() $u=u_0-\delta $
case of Proposition 2.2 gives an estimate contradicting (2.3).
$u=u_0-\delta $
case of Proposition 2.2 gives an estimate contradicting (2.3).
We thus turn to proving the modified statement with the extra condition that u is fixed.
For each nonnegative integer j, let
![]() $\mathcal {I}_j$
denote the interval
$\mathcal {I}_j$
denote the interval
Then our count of n is given by
 $$ \begin{align} \sum_{j\ge 0} \sum_{\substack{p \in \mathcal{I}_j \cap (x^{1/U'},y] \\p\equiv a\ \ \ \pmod{q}}} \sum_{\substack{n \le x\\P_k(n)=p}} 1.\end{align} $$
$$ \begin{align} \sum_{j\ge 0} \sum_{\substack{p \in \mathcal{I}_j \cap (x^{1/U'},y] \\p\equiv a\ \ \ \pmod{q}}} \sum_{\substack{n \le x\\P_k(n)=p}} 1.\end{align} $$
Let
![]() $\mathcal {J}$
be the collection of nonnegative integers j with
$\mathcal {J}$
be the collection of nonnegative integers j with
![]() $\mathcal {I}_j \subset (x^{1/U'}, y/\exp (\sqrt {\log {x}}))$
. Then, at the cost of another error of size
$\mathcal {I}_j \subset (x^{1/U'}, y/\exp (\sqrt {\log {x}}))$
. Then, at the cost of another error of size
![]() $o(x/\phi (q))$
, we can restrict the triple sum in (2.5) to
$o(x/\phi (q))$
, we can restrict the triple sum in (2.5) to
![]() $j \in \mathcal {J}$
. Indeed, the n counted by the triple sum above that are excluded by this restriction have either a prime divisor in
$j \in \mathcal {J}$
. Indeed, the n counted by the triple sum above that are excluded by this restriction have either a prime divisor in
![]() $P:=(x^{1/U'}, bx^{1/U'}]$
or in
$P:=(x^{1/U'}, bx^{1/U'}]$
or in
![]() ${P':=[y/b\exp (\sqrt {\log {x}}), y]}$
, and the number of such
${P':=[y/b\exp (\sqrt {\log {x}}), y]}$
, and the number of such
![]() $n\le x$
is at most
$n\le x$
is at most
 $$ \begin{align*}x\sum_{\substack{p \in P\cup P' \\ p\equiv a\ \ \ \pmod{q}}} 1/p = o(x/\phi(q)),\end{align*} $$
$$ \begin{align*}x\sum_{\substack{p \in P\cup P' \\ p\equiv a\ \ \ \pmod{q}}} 1/p = o(x/\phi(q)),\end{align*} $$
by partial summation and the Brun–Titchmarsh theorem (Proposition 2.3). We proceed to estimate, for each
![]() $j \in \mathcal {J}$
, the corresponding inner sums in (2.5) over p and n.
$j \in \mathcal {J}$
, the corresponding inner sums in (2.5) over p and n.
If p is prime and
![]() $P_k(n)=p$
, then
$P_k(n)=p$
, then
![]() $n=mp$
where
$n=mp$
where
![]() $m \le x/p$
,
$m \le x/p$
,
![]() $P_k(m) \le p$
, and
$P_k(m) \le p$
, and
![]() $P_{k-1}(m)\ge p$
. The converse also holds. Thus, if
$P_{k-1}(m)\ge p$
. The converse also holds. Thus, if
![]() $j \in \mathcal {J}$
and
$j \in \mathcal {J}$
and
![]() $p \in \mathcal {I}_j$
,
$p \in \mathcal {I}_j$
,
 $$\begin{align*}\sum_{\substack{n \le x\\P_k(n)=p}} 1 = \Psi_k(x/p,p) - \Psi_{k-1}(x/p,p-\epsilon) \end{align*}$$
$$\begin{align*}\sum_{\substack{n \le x\\P_k(n)=p}} 1 = \Psi_k(x/p,p) - \Psi_{k-1}(x/p,p-\epsilon) \end{align*}$$
for (say)
![]() $\epsilon = \frac {1}{2}$
. Hence,
$\epsilon = \frac {1}{2}$
. Hence,
 $$\begin{align*}\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}} \sum_{\substack{n\le x \\ P_k(n)=p}} 1 = \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}}\Psi_k(x/p,p) - \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}}\Psi_{k-1}(x/p,p-\epsilon). \end{align*}$$
$$\begin{align*}\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}} \sum_{\substack{n\le x \\ P_k(n)=p}} 1 = \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}}\Psi_k(x/p,p) - \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \pmod{q}}}\Psi_{k-1}(x/p,p-\epsilon). \end{align*}$$
To continue, observe that, for
![]() $j \in \mathcal {J}$
,
$j \in \mathcal {J}$
,
 $$ \begin{align*} &\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_k(x/p,p) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_k(x/t,t)\, \frac{\mathrm{d}t}{\log{t}} \\ &\qquad\qquad= \sum_{\substack{u_j \le p < v_j \\ p\equiv a\ \ \ \pmod{q}}}\sum_{\substack{n \le x/p \\ P_k(n) \le p}}1 - \frac{1}{\phi(q)}\int_{u_j}^{v_j} \sum_{\substack{n \le x/t \\ P_k(n) \le t}} \frac{1}{\log{t}}\,\mathrm{d}t \\ &\qquad\qquad= \sum_{n\le x/u_j} \left(\sum_{\substack{m < p \le M \\ p\equiv a\ \ \ \pmod{q}}} 1 - \frac{1}{\phi(q)} \int_{m}^{M}\frac{\mathrm{d}t}{\log{t}} + O(1) \right), \end{align*} $$
$$ \begin{align*} &\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_k(x/p,p) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_k(x/t,t)\, \frac{\mathrm{d}t}{\log{t}} \\ &\qquad\qquad= \sum_{\substack{u_j \le p < v_j \\ p\equiv a\ \ \ \pmod{q}}}\sum_{\substack{n \le x/p \\ P_k(n) \le p}}1 - \frac{1}{\phi(q)}\int_{u_j}^{v_j} \sum_{\substack{n \le x/t \\ P_k(n) \le t}} \frac{1}{\log{t}}\,\mathrm{d}t \\ &\qquad\qquad= \sum_{n\le x/u_j} \left(\sum_{\substack{m < p \le M \\ p\equiv a\ \ \ \pmod{q}}} 1 - \frac{1}{\phi(q)} \int_{m}^{M}\frac{\mathrm{d}t}{\log{t}} + O(1) \right), \end{align*} $$
where m and M are defined by
and where the last displayed sum on n is understood to be extended only over those
![]() $n\le x/u_j$
for which
$n\le x/u_j$
for which
![]() $m \le M$
. By the Siegel–Walfisz theorem (Proposition 2.4),
$m \le M$
. By the Siegel–Walfisz theorem (Proposition 2.4),
 $$\begin{align*}\sum_{\substack{m < p \le M \\ p\equiv a\ \ \ \pmod{q}}} 1 - \frac{1}{\phi(q)} \int_{m}^{M}\frac{\mathrm{d}t}{\log{t}} \ll M \exp(-C\sqrt{\log M}) \ll \frac{x}{n} \exp(-C'\sqrt{\log{x}}), \end{align*}$$
$$\begin{align*}\sum_{\substack{m < p \le M \\ p\equiv a\ \ \ \pmod{q}}} 1 - \frac{1}{\phi(q)} \int_{m}^{M}\frac{\mathrm{d}t}{\log{t}} \ll M \exp(-C\sqrt{\log M}) \ll \frac{x}{n} \exp(-C'\sqrt{\log{x}}), \end{align*}$$
where C is an absolute positive constant and
![]() $C'= C/\sqrt {U'}$
. (This use of the Siegel–Walfisz theorem explains the restriction
$C'= C/\sqrt {U'}$
. (This use of the Siegel–Walfisz theorem explains the restriction
![]() $q\le (\log {x})^A$
in the statement of Proposition 2.2.) Putting this back in the above and summing on n, we find that (for large x)
$q\le (\log {x})^A$
in the statement of Proposition 2.2.) Putting this back in the above and summing on n, we find that (for large x)
 $$ \begin{align} \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_k(x/p,p) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_k(x/t,t)\, \frac{\mathrm{d}t}{\log{t}} \ll x \log{x} \cdot \exp(-C'\sqrt{\log{x}}) + \frac{x}{u_j}. \end{align} $$
$$ \begin{align} \sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_k(x/p,p) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_k(x/t,t)\, \frac{\mathrm{d}t}{\log{t}} \ll x \log{x} \cdot \exp(-C'\sqrt{\log{x}}) + \frac{x}{u_j}. \end{align} $$
A nearly identical calculation gives the same bound for the difference
 $$ \begin{align*}\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_{k-1}(x/p,p-\epsilon) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_{k-1}(x/t,t)\, \frac{\mathrm{d}t}{\log{t}}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{p \in \mathcal{I}_j \\ p\equiv a\ \ \ \pmod{q}}}\Psi_{k-1}(x/p,p-\epsilon) - \frac{1}{\phi(q)}\int_{\mathcal{I}_j} \Psi_{k-1}(x/t,t)\, \frac{\mathrm{d}t}{\log{t}}.\end{align*} $$
Since
![]() $u_{j+1}/u_j \ge 2$
and the smallest
$u_{j+1}/u_j \ge 2$
and the smallest
![]() $j \in \mathcal {J}$
has
$j \in \mathcal {J}$
has
![]() $u_j \ge x^{1/U'}$
, the expression on the right-hand side of (2.6), when summed on
$u_j \ge x^{1/U'}$
, the expression on the right-hand side of (2.6), when summed on
![]() $j \in \mathcal {J}$
, is
$j \in \mathcal {J}$
, is
![]() $\ll x (\log {x})^2 \exp (-C'\sqrt {\log {x}}) + x^{1-1/U'}$
, and this is certainly
$\ll x (\log {x})^2 \exp (-C'\sqrt {\log {x}}) + x^{1-1/U'}$
, and this is certainly
![]() $o(x/\phi (q))$
. As a consequence, instead of our original triple sum (2.5), it is enough to estimate
$o(x/\phi (q))$
. As a consequence, instead of our original triple sum (2.5), it is enough to estimate
 $$ \begin{align} \frac{x}{\phi(q)} \sum_{j \in \mathcal{J}} \frac{1}{x}\int_{\mathcal{I}_j}(\Psi_k(x/t,t) - \Psi_{k-1}(x/t,t))\, \frac{\mathrm{d}t}{\log{t}}. \end{align} $$
$$ \begin{align} \frac{x}{\phi(q)} \sum_{j \in \mathcal{J}} \frac{1}{x}\int_{\mathcal{I}_j}(\Psi_k(x/t,t) - \Psi_{k-1}(x/t,t))\, \frac{\mathrm{d}t}{\log{t}}. \end{align} $$
We now apply Proposition 2.1, noting that for each
![]() $t \in \mathcal {I}_j$
, we have
$t \in \mathcal {I}_j$
, we have
![]() $\frac {\log {(x/t)}}{\log {t}} = \frac {\log {x}}{\log {t}}-1\le U'-1$
as well as
$\frac {\log {(x/t)}}{\log {t}} = \frac {\log {x}}{\log {t}}-1\le U'-1$
as well as
![]() $\log (x/t) \ge \log (y/t) \ge \sqrt {\log {x}}$
. We find that
$\log (x/t) \ge \log (y/t) \ge \sqrt {\log {x}}$
. We find that
 $$ \begin{align*} &\frac{1}{x}\int_{\mathcal{I}_j} (\Psi_k(x/t,t) - \Psi_{k-1}(x/t,t)) \frac{\mathrm{d}t}{\log{t}} \\ &\qquad= \int_{\mathcal{I}_j} \frac{1}{t} \left(\rho_k\left(\frac{\log{x}}{\log{t}}-1\right) - \rho_{k-1}\left(\frac{\log{x}}{\log{t}}-1\right)\right) \frac{\mathrm{d}t}{\log{t}} + O\left(\int_{\mathcal{I}_j} \frac{1}{t\sqrt{\log{x}}} \frac{\mathrm{d}t}{\log{t}}\right).\end{align*} $$
$$ \begin{align*} &\frac{1}{x}\int_{\mathcal{I}_j} (\Psi_k(x/t,t) - \Psi_{k-1}(x/t,t)) \frac{\mathrm{d}t}{\log{t}} \\ &\qquad= \int_{\mathcal{I}_j} \frac{1}{t} \left(\rho_k\left(\frac{\log{x}}{\log{t}}-1\right) - \rho_{k-1}\left(\frac{\log{x}}{\log{t}}-1\right)\right) \frac{\mathrm{d}t}{\log{t}} + O\left(\int_{\mathcal{I}_j} \frac{1}{t\sqrt{\log{x}}} \frac{\mathrm{d}t}{\log{t}}\right).\end{align*} $$
The error term, when summed on
![]() $j \in \mathcal {J}$
, is
$j \in \mathcal {J}$
, is
![]() $\ll \frac {1}{\sqrt {\log {x}}}\int _{2}^{x} \frac {\mathrm {d}t}{t\log {t}} \ll \log \log {x}/\sqrt {\log {x}}$
, and so is
$\ll \frac {1}{\sqrt {\log {x}}}\int _{2}^{x} \frac {\mathrm {d}t}{t\log {t}} \ll \log \log {x}/\sqrt {\log {x}}$
, and so is
![]() $o(1)$
; inserted back into (2.7), we see that this gives rise to a final error of size
$o(1)$
; inserted back into (2.7), we see that this gives rise to a final error of size
![]() $o(x/\phi (q))$
in our count, which is acceptable. To deal with the remaining integrals, we write
$o(x/\phi (q))$
in our count, which is acceptable. To deal with the remaining integrals, we write
![]() $u_j = x^{\mu _j}$
and
$u_j = x^{\mu _j}$
and
![]() $v_j = x^{\nu _j}$
and make the change of variables
$v_j = x^{\nu _j}$
and make the change of variables
![]() $\alpha = \frac {\log {x}}{\log {t}}$
. Then
$\alpha = \frac {\log {x}}{\log {t}}$
. Then
![]() $\mathrm {d}\alpha = -\frac {\log {x}}{t(\log {t})^2}\, \mathrm {d}t$
, so that
$\mathrm {d}\alpha = -\frac {\log {x}}{t(\log {t})^2}\, \mathrm {d}t$
, so that
![]() $\frac {\mathrm {d}t}{t\log {t}} = -\frac {\mathrm {d}\alpha }{\alpha }$
and
$\frac {\mathrm {d}t}{t\log {t}} = -\frac {\mathrm {d}\alpha }{\alpha }$
and
 $$ \begin{align*} & \sum_{j \in \mathcal{J}} \int_{\mathcal{I}_j} \frac{1}{t}\left(\rho_k\left(\frac{\log{x}}{\log{t}}-1\right) - \rho_{k-1}\left(\frac{\log{x}}{\log{t}}-1\right)\right) \frac{\mathrm{d}t}{\log{t}}\\[5pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad = \sum_{j \in \mathcal{J}} \int_{1/\mu_j}^{1/\nu_j} -\frac{\rho_k(\alpha-1)-\rho_{k-1}(\alpha-1)}{\alpha}\, \mathrm{d}\alpha. \end{align*} $$
$$ \begin{align*} & \sum_{j \in \mathcal{J}} \int_{\mathcal{I}_j} \frac{1}{t}\left(\rho_k\left(\frac{\log{x}}{\log{t}}-1\right) - \rho_{k-1}\left(\frac{\log{x}}{\log{t}}-1\right)\right) \frac{\mathrm{d}t}{\log{t}}\\[5pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad = \sum_{j \in \mathcal{J}} \int_{1/\mu_j}^{1/\nu_j} -\frac{\rho_k(\alpha-1)-\rho_{k-1}(\alpha-1)}{\alpha}\, \mathrm{d}\alpha. \end{align*} $$
From (2.1),
![]() $-\frac {\rho _k(\alpha -1)-\rho _{k-1}(\alpha -1)}{\alpha } = \rho _k'(\alpha )$
, so that this last sum on j simplifies to
$-\frac {\rho _k(\alpha -1)-\rho _{k-1}(\alpha -1)}{\alpha } = \rho _k'(\alpha )$
, so that this last sum on j simplifies to
![]() $\sum _{j \in \mathcal {J}} (\rho _k(1/\nu _j)-\rho _k(1/\mu _j))$
. Now, following [Reference Knuth and Trabb Pardo19], we introduce the function
$\sum _{j \in \mathcal {J}} (\rho _k(1/\nu _j)-\rho _k(1/\mu _j))$
. Now, following [Reference Knuth and Trabb Pardo19], we introduce the function
![]() $F_k(\beta)$
defined for
$F_k(\beta)$
defined for
![]() $\beta \in (0,1]$
by
$\beta \in (0,1]$
by
![]() $F_k(\beta)=\rho_k(1/\beta)$
. By the mean value theorem,
$F_k(\beta)=\rho_k(1/\beta)$
. By the mean value theorem,
 $$ \begin{align*} \rho_k(1/\nu_j) - \rho_k(1/\mu_j) &= F_k(\nu_j) - F_k(\mu_j) \\ &= (\nu_j-\mu_j) F_k'(t_j) = \frac{\log(1+D^{-1})}{\log{x}} F_k'(t_j)\end{align*} $$
$$ \begin{align*} \rho_k(1/\nu_j) - \rho_k(1/\mu_j) &= F_k(\nu_j) - F_k(\mu_j) \\ &= (\nu_j-\mu_j) F_k'(t_j) = \frac{\log(1+D^{-1})}{\log{x}} F_k'(t_j)\end{align*} $$
for some
![]() $t_j \in (\mu _j,\nu _j)$
. Thus,
$t_j \in (\mu _j,\nu _j)$
. Thus,
 $$ \begin{align*} \sum_{j \in \mathcal{J}} (\rho_k(1/\nu_j)-\rho_k(1/\mu_j)) &= \frac{\log(1+D^{-1})}{\log{b}}\sum_{j \in \mathcal{J}} F_k'(t_j) \cdot \frac{\log{b}}{\log{x}} \\\ &= \frac{\log(1+D^{-1})}{\log{b}}\sum_{j \in \mathcal{J}} F_k'(t_j) \cdot (\mu_{j+1}-\mu_j). \end{align*} $$
$$ \begin{align*} \sum_{j \in \mathcal{J}} (\rho_k(1/\nu_j)-\rho_k(1/\mu_j)) &= \frac{\log(1+D^{-1})}{\log{b}}\sum_{j \in \mathcal{J}} F_k'(t_j) \cdot \frac{\log{b}}{\log{x}} \\\ &= \frac{\log(1+D^{-1})}{\log{b}}\sum_{j \in \mathcal{J}} F_k'(t_j) \cdot (\mu_{j+1}-\mu_j). \end{align*} $$
Since each
![]() $t_j \in (\mu _j,\nu _j) \subset (\mu _j,\mu _{j+1})$
, the final sum on j is essentially a Riemann sum. To make this precise, let
$t_j \in (\mu _j,\nu _j) \subset (\mu _j,\mu _{j+1})$
, the final sum on j is essentially a Riemann sum. To make this precise, let
![]() $j_0 = \min \mathcal {J}$
and
$j_0 = \min \mathcal {J}$
and
![]() $j_1 = \max \mathcal {J}$
. Then
$j_1 = \max \mathcal {J}$
. Then
 $$\begin{align*}F_k'(1/U') \left(\mu_{j_0}-\frac{1}{U'}\right) + \sum_{j \in \mathcal{J}} F_k'(t_j) (\mu_{j+1}-\mu_j) + F_k'(1/u)\left(\frac{1}{u}-\mu_{j_1+1}\right) \end{align*}$$
$$\begin{align*}F_k'(1/U') \left(\mu_{j_0}-\frac{1}{U'}\right) + \sum_{j \in \mathcal{J}} F_k'(t_j) (\mu_{j+1}-\mu_j) + F_k'(1/u)\left(\frac{1}{u}-\mu_{j_1+1}\right) \end{align*}$$
is a genuine Riemann sum for
![]() $\int _{1/U'}^{1/u} F_k'(t)\, \mathrm {d}t$
, whose mesh size goes to
$\int _{1/U'}^{1/u} F_k'(t)\, \mathrm {d}t$
, whose mesh size goes to
![]() $0$
as
$0$
as
![]() $x \to \infty $
. However, the terms we have added to the sum on
$x \to \infty $
. However, the terms we have added to the sum on
![]() $j\in \mathcal {J}$
contribute
$j\in \mathcal {J}$
contribute
![]() $o(1)$
, as
$o(1)$
, as
![]() $x\to \infty $
. It follows that
$x\to \infty $
. It follows that
![]() $\sum _{j \in \mathcal {J}} F_k'(t_j) (\mu _{j+1}-\mu _j) \to \int _{1/U'}^{1/u} F_k'(t)\,\mathrm {d}t = F_k(1/u) - F_k(1/U') = \rho _k(u)-\rho _k(U')$
. Collecting estimates completes the proof of the proposition in the case when u is fixed.
$\sum _{j \in \mathcal {J}} F_k'(t_j) (\mu _{j+1}-\mu _j) \to \int _{1/U'}^{1/u} F_k'(t)\,\mathrm {d}t = F_k(1/u) - F_k(1/U') = \rho _k(u)-\rho _k(U')$
. Collecting estimates completes the proof of the proposition in the case when u is fixed.
To deduce Theorem 1.1, it remains to handle the contribution from n with
![]() ${P_k(n) \le x^{1/U'}}$
.
${P_k(n) \le x^{1/U'}}$
.
The following lemma bounds the number of integers with a large smooth divisor. A proof is sketched in Exercise 293 on page 554 of [Reference Tenenbaum26], with a solution in [Reference Tenenbaum25, pp. 305–306]. By the y-smooth part of a number n, we mean
![]() $\prod _{\substack {p^e\parallel n \\ p \le y}} p^e$
.
$\prod _{\substack {p^e\parallel n \\ p \le y}} p^e$
.
Lemma 2.5 For all
![]() $x\ge z\ge y\ge 2$
, the number of
$x\ge z\ge y\ge 2$
, the number of
![]() $n\le x$
whose y-smooth part exceeds z is
$n\le x$
whose y-smooth part exceeds z is
![]() $O\left (x \exp \left (-\frac {1}{2}\frac {\log {z}}{\log {y}}\right )\right )$
.
$O\left (x \exp \left (-\frac {1}{2}\frac {\log {z}}{\log {y}}\right )\right )$
.
Lemma 2.6 Fix a positive integer k and a real number
![]() $B \ge 1$
.
$B \ge 1$
.
-
• When
 $k=1$
, the number of
$k=1$
, the number of
 $n\le x$
with
$n\le x$
with
 $P_k(n) \le y$
and
$P_k(n) \le y$
and
 $P_k(n)\equiv a\ \pmod {q}$
is uniformly for
$P_k(n)\equiv a\ \pmod {q}$
is uniformly for $$\begin{align*}\ll \frac{x}{\phi(q)} \exp\left(-\frac{1}{8}u\right) + x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp\left(-\frac{1}{8}u\right), \end{align*}$$
$$\begin{align*}\ll \frac{x}{\phi(q)} \exp\left(-\frac{1}{8}u\right) + x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp\left(-\frac{1}{8}u\right), \end{align*}$$
 $x\ge y \ge 3$
with
$x\ge y \ge 3$
with
 $y\le x^{1/4}$
, and
$y\le x^{1/4}$
, and
 $a\bmod {q}$
any coprime residue class with
$a\bmod {q}$
any coprime residue class with
 $q\le x^{1/8}$
. As usual,
$q\le x^{1/8}$
. As usual,
 $u = \frac {\log {x}}{\log {y}}$
.
$u = \frac {\log {x}}{\log {y}}$
.
-
• When
 $k\ge 2$
, the number of
$k\ge 2$
, the number of
 $n\le x$
with
$n\le x$
with
 $P_k(n) \le y$
and
$P_k(n) \le y$
and
 $P_k(n)\equiv a\ \pmod {q}$
is uniformly in the same range of
$P_k(n)\equiv a\ \pmod {q}$
is uniformly in the same range of $$\begin{align*}\ll \frac{x}{\log{x}}(\log\log{x})^{k-2} \log{(3q)} + \frac{x}{\phi(q)} \frac{(\log{u})^{k-2}}{u}, \end{align*}$$
$$\begin{align*}\ll \frac{x}{\log{x}}(\log\log{x})^{k-2} \log{(3q)} + \frac{x}{\phi(q)} \frac{(\log{u})^{k-2}}{u}, \end{align*}$$
 $x,y$
, and q.
$x,y$
, and q.
Proof We will restrict attention to
![]() $n> x^{3/4}$
; this is permissible, since
$n> x^{3/4}$
; this is permissible, since
![]() $x^{3/4}$
is dwarfed by either of our target upper bounds. We let
$x^{3/4}$
is dwarfed by either of our target upper bounds. We let
![]() $p = P_k(n)$
and write
$p = P_k(n)$
and write
![]() $n = p_1\cdots p_{k-1} p s$
, where
$n = p_1\cdots p_{k-1} p s$
, where
![]() $p_1 \geq p_2 \geq \dots \ge p_{k-1} \ge p$
and
$p_1 \geq p_2 \geq \dots \ge p_{k-1} \ge p$
and
![]() $P(s) \le p$
.
$P(s) \le p$
.
We first show that we can assume
![]() $s \le x^{1/2}$
. Indeed, suppose
$s \le x^{1/2}$
. Indeed, suppose
![]() $s> x^{1/2}$
. Then, with
$s> x^{1/2}$
. Then, with
![]() $m=n/p$
, we have that
$m=n/p$
, we have that
![]() $m \le x/p$
and that the p-smooth part of m exceeds
$m \le x/p$
and that the p-smooth part of m exceeds
![]() $x^{1/2}$
. Applying Lemma 2.5, we see that for every
$x^{1/2}$
. Applying Lemma 2.5, we see that for every
![]() $p \le y$
, the number of corresponding m is
$p \le y$
, the number of corresponding m is
 $$ \begin{align*} \ll \frac{x}{p}\exp\left(-\frac{1}{4}\frac{\log{x}}{\log{p}}\right) &\ll \frac{x}{p}\exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \cdot \exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \\ &\ll \frac{x}{(\log{x})^{B}} \frac{(\log{p})^B}{p} \exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \\ &\ll \frac{x}{(\log{x})^{B}} \frac{(\log{p})^B}{p} \exp\left(-\frac{1}{8}u\right)\!. \end{align*} $$
$$ \begin{align*} \ll \frac{x}{p}\exp\left(-\frac{1}{4}\frac{\log{x}}{\log{p}}\right) &\ll \frac{x}{p}\exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \cdot \exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \\ &\ll \frac{x}{(\log{x})^{B}} \frac{(\log{p})^B}{p} \exp\left(-\frac{1}{8}\frac{\log{x}}{\log{p}}\right) \\ &\ll \frac{x}{(\log{x})^{B}} \frac{(\log{p})^B}{p} \exp\left(-\frac{1}{8}u\right)\!. \end{align*} $$
Now, we sum on
![]() $p \le y$
with
$p \le y$
with
![]() $p\equiv a\ \pmod {q}$
. We split the sum at
$p\equiv a\ \pmod {q}$
. We split the sum at
![]() $3q^2$
, using Mertens’ theorem to bound the first half and the Brun–Titchmarsh theorem (with partial summation) for the second; this gives
$3q^2$
, using Mertens’ theorem to bound the first half and the Brun–Titchmarsh theorem (with partial summation) for the second; this gives
 $$ \begin{align*} \sum_{\substack{p \le y \\p \equiv a\ \ \ \pmod{q}}} \frac{(\log{p})^B}{p} &\le \sum_{p \le 3q^2} \frac{(\log{p})^B}{p} + \sum_{\substack{3q^2 < p \le y \\ p \equiv a\ \ \ \pmod{q}}} \frac{(\log{p})^B}{p} \\ &\ll (\log(3q))^{B-1} \sum_{p \le 3q^2} \frac{\log{p}}{p} + \frac{1}{\phi(q)} (\log{y})^{B} \\&\ll (\log{(3q)})^{B} + \frac{(\log{y})^{B}}{\phi(q)}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{p \le y \\p \equiv a\ \ \ \pmod{q}}} \frac{(\log{p})^B}{p} &\le \sum_{p \le 3q^2} \frac{(\log{p})^B}{p} + \sum_{\substack{3q^2 < p \le y \\ p \equiv a\ \ \ \pmod{q}}} \frac{(\log{p})^B}{p} \\ &\ll (\log(3q))^{B-1} \sum_{p \le 3q^2} \frac{\log{p}}{p} + \frac{1}{\phi(q)} (\log{y})^{B} \\&\ll (\log{(3q)})^{B} + \frac{(\log{y})^{B}}{\phi(q)}. \end{align*} $$
Substituting this estimate into the previous display, we conclude that the n with
![]() ${s> x^{1/2}}$
contribute
${s> x^{1/2}}$
contribute
 $$ \begin{align} \ll \frac{x}{u^B \phi(q)} \exp(-\frac{1}{8}u) &+ x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp(-\frac{1}{8}u) \notag \\ &\ll \frac{x}{\phi(q)} \exp\left(-\frac{1}{8}u\right) + x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp\left(-\frac{1}{8}u\right). \end{align} $$
$$ \begin{align} \ll \frac{x}{u^B \phi(q)} \exp(-\frac{1}{8}u) &+ x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp(-\frac{1}{8}u) \notag \\ &\ll \frac{x}{\phi(q)} \exp\left(-\frac{1}{8}u\right) + x \left(\frac{\log(3q)}{\log{x}}\right)^B \cdot \exp\left(-\frac{1}{8}u\right). \end{align} $$
This is already enough to settle the
![]() $k=1$
case of Lemma 2.6. Indeed, in that case,
$k=1$
case of Lemma 2.6. Indeed, in that case,
![]() $n=ps$
, where
$n=ps$
, where
![]() $p = P(n)$
, and
$p = P(n)$
, and
![]() $s = n/P(n) \ge n/y> x^{3/4}/y \ge x^{1/2}$
.
$s = n/P(n) \ge n/y> x^{3/4}/y \ge x^{1/2}$
.
Now, suppose that
![]() $k \ge 2$
and that
$k \ge 2$
and that
![]() $s \le x^{1/2}$
. Then
$s \le x^{1/2}$
. Then
so that
![]() $p_1 \ge x^{1/4k}$
. Hence, given
$p_1 \ge x^{1/4k}$
. Hence, given
![]() $p_2,\dots ,p_{k-1},p$
, and s, the number of possibilities for
$p_2,\dots ,p_{k-1},p$
, and s, the number of possibilities for
![]() $p_1$
(and thus also for n) is
$p_1$
(and thus also for n) is
![]() $\ll \pi (x/p_2\cdots p_{k-1} p s) \ll x/p_2 \cdots p_{k-1} p s\log {x}$
. Observe that s is p-smooth, while each
$\ll \pi (x/p_2\cdots p_{k-1} p s) \ll x/p_2 \cdots p_{k-1} p s\log {x}$
. Observe that s is p-smooth, while each
![]() $p_i \in [p,x]$
. We have that
$p_i \in [p,x]$
. We have that
![]() $\sum _{s\ p\text {-smooth}} 1/s = \prod _{\text {prime }\ell \le p} (1-1/\ell )^{-1} \ll \log {p}$
. Moreover (when
$\sum _{s\ p\text {-smooth}} 1/s = \prod _{\text {prime }\ell \le p} (1-1/\ell )^{-1} \ll \log {p}$
. Moreover (when
![]() $p \le y$
),
$p \le y$
),
![]() $\sum _{p \le p_i \le x} 1/p_i \ll \log \frac {\log {x}}{\log {p}}$
. Hence, the number of possibilities for n given p is
$\sum _{p \le p_i \le x} 1/p_i \ll \log \frac {\log {x}}{\log {p}}$
. Hence, the number of possibilities for n given p is
 $$\begin{align*}\ll \frac{x}{\log{x}} \left(\log \frac{\log{x}}{\log{p}}\right)^{k-2} \frac{\log{p}}{p}. \end{align*}$$
$$\begin{align*}\ll \frac{x}{\log{x}} \left(\log \frac{\log{x}}{\log{p}}\right)^{k-2} \frac{\log{p}}{p}. \end{align*}$$
We now sum on
![]() $p\le y$
with
$p\le y$
with
![]() $p\equiv a\ \pmod {q}$
. Estimating crudely, we see that the
$p\equiv a\ \pmod {q}$
. Estimating crudely, we see that the
![]() $p\le 3q^2$
contribute
$p\le 3q^2$
contribute
To handle the remaining contribution in the case when
![]() $y> 3q^2$
, we apply partial summation; by Brun–Titchmarsh,
$y> 3q^2$
, we apply partial summation; by Brun–Titchmarsh,
 $$ \begin{align*} &\sum_{\substack{3q^2 < p \le y\\p\equiv a\ \ \ \pmod{q}}} \left(\log \frac{\log{x}}{\log{p}}\right)^{k-2} \frac{\log{p}}{p} \\ &\qquad\qquad\qquad\qquad\ll \frac{1}{\phi(q)} (\log{u})^{k-2} -\int_{3q^2}^{y} \pi(t;q,a) \mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right).\end{align*} $$
$$ \begin{align*} &\sum_{\substack{3q^2 < p \le y\\p\equiv a\ \ \ \pmod{q}}} \left(\log \frac{\log{x}}{\log{p}}\right)^{k-2} \frac{\log{p}}{p} \\ &\qquad\qquad\qquad\qquad\ll \frac{1}{\phi(q)} (\log{u})^{k-2} -\int_{3q^2}^{y} \pi(t;q,a) \mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right).\end{align*} $$
Since
![]() $\left (\log \frac {\log {x}}{\log {t}}\right )^{k-2} \frac {\log {t}}{t}$
is a decreasing function of t on
$\left (\log \frac {\log {x}}{\log {t}}\right )^{k-2} \frac {\log {t}}{t}$
is a decreasing function of t on
![]() $[3q^2,y]$
, the bound
$[3q^2,y]$
, the bound
![]() $\pi (t;q,a) \ll t/\phi (q)\log {t}$
implies that
$\pi (t;q,a) \ll t/\phi (q)\log {t}$
implies that
 $$ \begin{align*} &-\int_{3q^2}^{y} \pi(t;q,a) \, \mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ll -\frac{1}{\phi(q)} \int_{3q^2}^{y} \frac{t}{\log{t}} \,\mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right). \end{align*} $$
$$ \begin{align*} &-\int_{3q^2}^{y} \pi(t;q,a) \, \mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ll -\frac{1}{\phi(q)} \int_{3q^2}^{y} \frac{t}{\log{t}} \,\mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right). \end{align*} $$
Integrating by parts again,
 $$ \begin{align*} &\int_{3q^2}^{y} \frac{t}{\log{t}}\,\mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right) \\ &\qquad\qquad\qquad\qquad=-\int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t} \, \mathrm{d}\left(\frac{t}{\log{t}}\right)+ O((\log\log{x})^{k-2}) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ll \int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \, \frac{\mathrm{d}t}{t} + O((\log\log{x})^{k-2}).\end{align*} $$
$$ \begin{align*} &\int_{3q^2}^{y} \frac{t}{\log{t}}\,\mathrm{d}\left(\left(\log \frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t}\right) \\ &\qquad\qquad\qquad\qquad=-\int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \frac{\log{t}}{t} \, \mathrm{d}\left(\frac{t}{\log{t}}\right)+ O((\log\log{x})^{k-2}) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ll \int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \, \frac{\mathrm{d}t}{t} + O((\log\log{x})^{k-2}).\end{align*} $$
Making the change of variables
![]() $\alpha = \frac {\log {t}}{\log {x}}$
,
$\alpha = \frac {\log {t}}{\log {x}}$
,
 $$\begin{align*}\int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \, \frac{\mathrm{d}t}{t} \le \log{x} \int_{0}^{1/u} (\log(1/\alpha))^{k-2}\, \mathrm{d}\alpha \ll \log{x} \cdot \frac{1}{u} (\log u)^{k-2}. \end{align*}$$
$$\begin{align*}\int_{3q^2}^{y} \left(\log\frac{\log{x}}{\log{t}}\right)^{k-2} \, \frac{\mathrm{d}t}{t} \le \log{x} \int_{0}^{1/u} (\log(1/\alpha))^{k-2}\, \mathrm{d}\alpha \ll \log{x} \cdot \frac{1}{u} (\log u)^{k-2}. \end{align*}$$
(In the last step, we use that
![]() $\int _{0}^{z} (\log (1/\alpha ))^{k-2}\,\mathrm {d}\alpha $
has the form
$\int _{0}^{z} (\log (1/\alpha ))^{k-2}\,\mathrm {d}\alpha $
has the form
![]() $z\cdot Q(\log (1/z))$
, where Q is a monic polynomial with degree
$z\cdot Q(\log (1/z))$
, where Q is a monic polynomial with degree
![]() $k-2$
.) Collecting estimates, we conclude that when
$k-2$
.) Collecting estimates, we conclude that when
![]() $k\ge 2$
, the n with
$k\ge 2$
, the n with
![]() $s \le x^{1/2}$
make a contribution
$s \le x^{1/2}$
make a contribution
 $$\begin{align*}\ll \frac{x}{\log{x}} (\log\log{x})^{k-2}\log{(3q)} + \frac{x}{\phi(q)} \frac{(\log{u})^{k-2}}{u}.\end{align*}$$
$$\begin{align*}\ll \frac{x}{\log{x}} (\log\log{x})^{k-2}\log{(3q)} + \frac{x}{\phi(q)} \frac{(\log{u})^{k-2}}{u}.\end{align*}$$
Since this upper bound dominates the contribution (2.8) from n with
![]() $s> x^{1/2}$
, the
$s> x^{1/2}$
, the
![]() $k\ge 2$
cases of Lemma 2.6 follow.
$k\ge 2$
cases of Lemma 2.6 follow.
Proof of Theorem 1.1
Fix
![]() $\eta> 0$
. We will show that the count of n in question is eventuallyFootnote
2
larger than
$\eta> 0$
. We will show that the count of n in question is eventuallyFootnote
2
larger than
![]() $\frac {1}{\phi (q)} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho _k(u)-\eta \right )x$
and eventually smaller than
$\frac {1}{\phi (q)} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho _k(u)-\eta \right )x$
and eventually smaller than
![]() $\frac {1}{\phi (q)} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho _k(u)+\eta \right )x$
, and hence is
$\frac {1}{\phi (q)} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho _k(u)+\eta \right )x$
, and hence is
![]() $\sim \frac {1}{\phi (q)}\frac {\log (1+D^{-1})}{\log {b}} \rho _k(u) x$
. Since
$\sim \frac {1}{\phi (q)}\frac {\log (1+D^{-1})}{\log {b}} \rho _k(u) x$
. Since
![]() $\Psi _k(x,y) \sim \rho _k(u) x$
, Theorem 1.1 then follows.
$\Psi _k(x,y) \sim \rho _k(u) x$
, Theorem 1.1 then follows.
The required lower bound is immediate from Proposition 2.2: it suffices to apply that proposition with
![]() $U'$
fixed large enough that
$U'$
fixed large enough that
![]() $\rho _k(U') < \eta $
.
$\rho _k(U') < \eta $
.
We turn now to the upper bound. Apply Lemma 2.6, taking
![]() $B=A+1$
in the case
$B=A+1$
in the case
![]() $k=1$
. That lemma implies the existence of a constant C, depending only on k (and on A, if
$k=1$
. That lemma implies the existence of a constant C, depending only on k (and on A, if
![]() $k=1$
) such that the following holds: for any fixed
$k=1$
) such that the following holds: for any fixed
![]() $U'\ge 4$
, the number of
$U'\ge 4$
, the number of
![]() $n\le x$
with
$n\le x$
with
![]() $P_k(n) \equiv a\ \pmod {q}$
and
$P_k(n) \equiv a\ \pmod {q}$
and
![]() $P_k(n) \le x^{1/U'}$
is eventually at most
$P_k(n) \le x^{1/U'}$
is eventually at most
![]() $C \frac {x}{\phi (q)} \frac {(\log {U'})^{k-2}}{U'}$
. If we choose
$C \frac {x}{\phi (q)} \frac {(\log {U'})^{k-2}}{U'}$
. If we choose
![]() $U'> U$
so large that
$U'> U$
so large that
![]() $C \frac {(\log {U'})^{k-2}}{U'} < \eta \frac {\log (1+D^{-1})}{\log {b}}$
, the desired upper bound then follows from Proposition 2.2.
$C \frac {(\log {U'})^{k-2}}{U'} < \eta \frac {\log (1+D^{-1})}{\log {b}}$
, the desired upper bound then follows from Proposition 2.2.
3 Benford’s law for the sum of the prime factors: proof of Theorem 1.2
For multiplicative functions
![]() $F,G$
taking values on or inside the complex unit circle, we define (following [Reference Granville and Soundararajan13]) the distance between F and G, up to x, by
$F,G$
taking values on or inside the complex unit circle, we define (following [Reference Granville and Soundararajan13]) the distance between F and G, up to x, by
 $$\begin{align*}\mathbb{D}(F,G;x) = \sqrt{\sum_{p \le x} \frac{1-\mathop{\mathrm{Re}}(F(p)\overline{G(p)})}{p}}. \end{align*}$$
$$\begin{align*}\mathbb{D}(F,G;x) = \sqrt{\sum_{p \le x} \frac{1-\mathop{\mathrm{Re}}(F(p)\overline{G(p)})}{p}}. \end{align*}$$
The following statement (Corollary 4.12 on page 494 of [Reference Tenenbaum26]), due to Montgomery and Tenenbaum, makes quantitatively precise a result of Halász [Reference Halász14] that F has mean value
![]() $0$
unless F “pretends” to be
$0$
unless F “pretends” to be
![]() $n^{it}$
for some t.
$n^{it}$
for some t.
Proposition 3.1 Let F be a multiplicative function with
![]() $|F(n)|\le 1$
for all n. For
$|F(n)|\le 1$
for all n. For
![]() $x\ge 2$
and
$x\ge 2$
and
![]() $T\ge 2$
, let
$T\ge 2$
, let
Then
 $$\begin{align*}\sum_{n \le x} F(n) \ll x \frac{1+m(x,T)}{\mathrm{e}^{m(x,T)}}+ \frac{x}{T}. \end{align*}$$
$$\begin{align*}\sum_{n \le x} F(n) \ll x \frac{1+m(x,T)}{\mathrm{e}^{m(x,T)}}+ \frac{x}{T}. \end{align*}$$
Here, the implied constant is absolute.
When F is real-valued, the following (slightly weakened version of a) theorem of Hall and Tenenbaum [Reference Hall and Tenenbaum16] allows us to consider only
![]() $\mathbb {D}(F,1;x)$
.
$\mathbb {D}(F,1;x)$
.
Proposition 3.2 Let F be a real-valued multiplicative function with
![]() $|F(n)|\le 1$
for all n. Then
$|F(n)|\le 1$
for all n. Then
Lemma 3.3 Fix
![]() $\delta> 0$
and fix
$\delta> 0$
and fix
![]() $U\ge 1$
. For all large x, the number of
$U\ge 1$
. For all large x, the number of
![]() $n\le x$
with
$n\le x$
with
![]() $P(n)\le y$
and
$P(n)\le y$
and
![]() $A(n)\equiv a\ \pmod {q}$
is
$A(n)\equiv a\ \pmod {q}$
is
 $$\begin{align*}\frac{\Psi(x,y)}{q}+ O(x/(\log{x})^{\frac{1}{2}-\delta}), \end{align*}$$
$$\begin{align*}\frac{\Psi(x,y)}{q}+ O(x/(\log{x})^{\frac{1}{2}-\delta}), \end{align*}$$
for all
![]() $x\ge y \ge x^{1/U}$
and residue classes
$x\ge y \ge x^{1/U}$
and residue classes
![]() $a\bmod {q}$
with
$a\bmod {q}$
with
![]() $q\le \log {x}$
.
$q\le \log {x}$
.
Proof By the orthogonality relations for additive characters,

Hence, it suffices to show that
for each nonzero residue class
![]() $r\bmod {q}$
.
$r\bmod {q}$
.
Write
![]() $r/q = r'/q'$
in lowest terms, so that
$r/q = r'/q'$
in lowest terms, so that
![]() $q'> 1$
. If
$q'> 1$
. If
![]() $q'=2$
, then
$q'=2$
, then
![]() $r'=1$
, and
$r'=1$
, and
![]() is a real-valued multiplicative function of modulus at most
is a real-valued multiplicative function of modulus at most
![]() $1$
. Moreover,
$1$
. Moreover,
![]() $\mathbb {D}(F,1;x)^2 \ge \sum _{2 < p \le y} 2/p = 2\log \log {x} + O(1)$
. By Proposition 3.2, the left-hand side of (3.1) is
$\mathbb {D}(F,1;x)^2 \ge \sum _{2 < p \le y} 2/p = 2\log \log {x} + O(1)$
. By Proposition 3.2, the left-hand side of (3.1) is
![]() $O(x/(\log {x})^{0.6})$
, which is more than we need. So we may assume
$O(x/(\log {x})^{0.6})$
, which is more than we need. So we may assume
![]() $q'> 2$
.
$q'> 2$
.
When
![]() $q'>2$
, we apply Proposition 3.1 taking
$q'>2$
, we apply Proposition 3.1 taking
![]() $T=\log {x}$
. Let t be any real number with
$T=\log {x}$
. Let t be any real number with
![]() $|t|\le T$
. We set
$|t|\le T$
. We set
![]() $z= \exp ((\log {x})^{\delta })$
and start from the lower bound
$z= \exp ((\log {x})^{\delta })$
and start from the lower bound
 $$ \begin{align} \mathbb{D}(F, n^{it}; x)^2 \ge \sum_{z < p \le y} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} p^{-it})}{p}. \end{align} $$
$$ \begin{align} \mathbb{D}(F, n^{it}; x)^2 \ge \sum_{z < p \le y} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} p^{-it})}{p}. \end{align} $$
To estimate the right-hand sum, we split the range of summation into blocks on which
![]() $p^{-it}$
is essentially constant.
$p^{-it}$
is essentially constant.
Cover
![]() $(z,y]$
with intervals
$(z,y]$
with intervals
![]() $\mathcal {I}= (u,u(1+1/(\log {x})^2)]$
, allowing the rightmost interval to jut out slightly past y but no further than
$\mathcal {I}= (u,u(1+1/(\log {x})^2)]$
, allowing the rightmost interval to jut out slightly past y but no further than
![]() $y+y/(\log {x})^2$
. On each interval
$y+y/(\log {x})^2$
. On each interval
![]() $\mathcal {I}$
, every
$\mathcal {I}$
, every
![]() $p \in \mathcal {I}$
satisfies
$p \in \mathcal {I}$
satisfies
![]() $|t\log {p} - t\log {u}| \le |t|/(\log {x})^2 \le 1/\log {x}$
, so that
$|t\log {p} - t\log {u}| \le |t|/(\log {x})^2 \le 1/\log {x}$
, so that
 $$\begin{align*}|p^{-it} - u^{-it}| = \left|\int_{t \log{u}}^{t\log{p}} \exp(-i\theta)\,d\theta\right| \le 1/\log{x} ,\end{align*}$$
$$\begin{align*}|p^{-it} - u^{-it}| = \left|\int_{t \log{u}}^{t\log{p}} \exp(-i\theta)\,d\theta\right| \le 1/\log{x} ,\end{align*}$$
and
 $$ \begin{align} \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} p^{-it})}{p} = \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} + O\left(\frac{1}{\log{x}}\sum_{p \in \mathcal{I}} \frac{1}{p}\right).\end{align} $$
$$ \begin{align} \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} p^{-it})}{p} = \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} + O\left(\frac{1}{\log{x}}\sum_{p \in \mathcal{I}} \frac{1}{p}\right).\end{align} $$
The error term when summed over all intervals
![]() $\mathcal {I}$
will be
$\mathcal {I}$
will be
![]() $O(\log \log {x}/\log {x})$
, which is negligible for us. So we focus on the main term. Observe that
$O(\log \log {x}/\log {x})$
, which is negligible for us. So we focus on the main term. Observe that
![]() $p = (1+o(1))u$
for every
$p = (1+o(1))u$
for every
![]() $p \in \mathcal {I}$
. (Here and below, asymptotic notation refers to the behavior as
$p \in \mathcal {I}$
. (Here and below, asymptotic notation refers to the behavior as
![]() $x\to \infty $
.) Thus,
$x\to \infty $
.) Thus,
 $$ \begin{align*} \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} &\gtrsim \frac{1}{u} \sum_{p \in \mathcal{I}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})) \\&\gtrsim \frac{1}{u} \sum_{\substack{a'\bmod{q'} \\ \gcd(a',q')=1}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' a'/q'} u^{-it})) \pi(\mathcal{I};q',a'), \end{align*} $$
$$ \begin{align*} \sum_{p \in \mathcal{I}} \frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} &\gtrsim \frac{1}{u} \sum_{p \in \mathcal{I}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})) \\&\gtrsim \frac{1}{u} \sum_{\substack{a'\bmod{q'} \\ \gcd(a',q')=1}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' a'/q'} u^{-it})) \pi(\mathcal{I};q',a'), \end{align*} $$
where
![]() $\pi (\mathcal {I};q',a')$
denotes the number of primes
$\pi (\mathcal {I};q',a')$
denotes the number of primes
![]() $p \in \mathcal {I}$
with
$p \in \mathcal {I}$
with
![]() $p\equiv a'\ \pmod {q'}$
. By the Siegel–Walfisz theorem (Proposition 2.4),
$p\equiv a'\ \pmod {q'}$
. By the Siegel–Walfisz theorem (Proposition 2.4),
![]() $\pi (\mathcal {I};q',a') \sim \frac {1}{\phi (q')} \pi (\mathcal {I})$
, where
$\pi (\mathcal {I};q',a') \sim \frac {1}{\phi (q')} \pi (\mathcal {I})$
, where
![]() $\pi (\mathcal {I})$
is the total count of primes belonging to
$\pi (\mathcal {I})$
is the total count of primes belonging to
![]() $\mathcal {I}$
. Thus, the above right-hand side is
$\mathcal {I}$
. Thus, the above right-hand side is
 $$ \begin{align}\gtrsim \frac{\pi(\mathcal{I})}{\phi(q') u} \sum_{\substack{a'\bmod{q'} \\ \gcd(a',q')=1}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' a'/q'} u^{-it})) &= \frac{\pi(\mathcal{I})}{\phi(q') u} (\phi(q') - \mathop{\mathrm{Re}}(\mu(q') u^{-it})) \notag\\ &\ge \frac{1}{2} \pi(\mathcal{I})/u \gtrsim \frac{1}{2} \sum_{p \in \mathcal{I}}\frac{1}{p}; \end{align} $$
$$ \begin{align}\gtrsim \frac{\pi(\mathcal{I})}{\phi(q') u} \sum_{\substack{a'\bmod{q'} \\ \gcd(a',q')=1}} (1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' a'/q'} u^{-it})) &= \frac{\pi(\mathcal{I})}{\phi(q') u} (\phi(q') - \mathop{\mathrm{Re}}(\mu(q') u^{-it})) \notag\\ &\ge \frac{1}{2} \pi(\mathcal{I})/u \gtrsim \frac{1}{2} \sum_{p \in \mathcal{I}}\frac{1}{p}; \end{align} $$
here, we use that
![]() $\sum _{a'\ \pmod {q'},~\gcd (a',q')=1} \mathrm {e}^{2\pi i a' r'/q'} = \mu (q')$
(see, for example, [Reference Hardy and Wright17, Theorem 272, p. 309]) and that
$\sum _{a'\ \pmod {q'},~\gcd (a',q')=1} \mathrm {e}^{2\pi i a' r'/q'} = \mu (q')$
(see, for example, [Reference Hardy and Wright17, Theorem 272, p. 309]) and that
![]() $\phi (q') - \mathop {\mathrm {Re}}(\mu (q') u^{-it}) \ge \phi (q')-1 \ge \frac {1}{2}\phi (q')$
, as
$\phi (q') - \mathop {\mathrm {Re}}(\mu (q') u^{-it}) \ge \phi (q')-1 \ge \frac {1}{2}\phi (q')$
, as
![]() $q'> 2$
. Combining the last two displays and summing on
$q'> 2$
. Combining the last two displays and summing on
![]() $\mathcal {I}$
,
$\mathcal {I}$
,
 $$ \begin{align*} \sum_{\mathcal{I}} \sum_{p \in \mathcal{I}}\frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} \gtrsim \frac{1}{2} \sum_{\mathcal{I}} \sum_{p \in \mathcal{I}}\frac{1}{p} \ge \frac{1}{2}\sum_{z < p \le y} \frac{1}{p} \gtrsim \frac{1}{2}(1-\delta)\log\log{x}. \end{align*} $$
$$ \begin{align*} \sum_{\mathcal{I}} \sum_{p \in \mathcal{I}}\frac{1-\mathop{\mathrm{Re}}(\mathrm{e}^{2\pi i r' p/q'} u^{-it})}{p} \gtrsim \frac{1}{2} \sum_{\mathcal{I}} \sum_{p \in \mathcal{I}}\frac{1}{p} \ge \frac{1}{2}\sum_{z < p \le y} \frac{1}{p} \gtrsim \frac{1}{2}(1-\delta)\log\log{x}. \end{align*} $$
From (3.3) (and the immediately following remark about the error term), the same lower bound holds for
![]() $\sum _{\mathcal {I}}\sum _{p \in \mathcal {I}} \frac {1-\mathop {\mathrm {Re}}(\mathrm {e}^{2\pi i r' p/q'} p^{-it})}{p}$
. This double sum essentially coincides with the right-hand side of (3.2), except for possibly including contributions from a few values of
$\sum _{\mathcal {I}}\sum _{p \in \mathcal {I}} \frac {1-\mathop {\mathrm {Re}}(\mathrm {e}^{2\pi i r' p/q'} p^{-it})}{p}$
. This double sum essentially coincides with the right-hand side of (3.2), except for possibly including contributions from a few values of
![]() $p> y$
. However, those contributions are
$p> y$
. However, those contributions are
![]() $O(1)$
, in fact
$O(1)$
, in fact
![]() $\ll \sum _{y < p < y+y/(\log {x})^2} 1/p \ll 1/(\log {x})^2$
. Thus,
$\ll \sum _{y < p < y+y/(\log {x})^2} 1/p \ll 1/(\log {x})^2$
. Thus,
![]() $\mathbb {D}(F,n^{it};x)^2 \gtrsim \frac {1}{2}(1-\delta )\log \log {x}$
. In particular,
$\mathbb {D}(F,n^{it};x)^2 \gtrsim \frac {1}{2}(1-\delta )\log \log {x}$
. In particular,
![]() $\mathbb {D}(F,n^{it};x)^2 \ge (\frac {1}{2}-\frac {9}{10}\delta )\log \log {x}$
once x is sufficiently large (in terms of
$\mathbb {D}(F,n^{it};x)^2 \ge (\frac {1}{2}-\frac {9}{10}\delta )\log \log {x}$
once x is sufficiently large (in terms of
![]() $\delta $
and U). Since this lower bound holds uniformly in t with
$\delta $
and U). Since this lower bound holds uniformly in t with
![]() $|t| \le T$
, the desired inequality (3.1) follows from Proposition 3.1.
$|t| \le T$
, the desired inequality (3.1) follows from Proposition 3.1.
Using Lemma 3.3, we can establish the following
![]() $A(n)$
-analogue of Proposition 2.2.
$A(n)$
-analogue of Proposition 2.2.
Proposition 3.4 Fix positive integers
![]() $k,D$
, and b with
$k,D$
, and b with
![]() $b\ge 2$
. Fix real numbers
$b\ge 2$
. Fix real numbers
![]() $U'> U \ge 1$
, and fix
$U'> U \ge 1$
, and fix
![]() $\epsilon> 0$
. The number of
$\epsilon> 0$
. The number of
![]() $n\le x$
for which
$n\le x$
for which
![]() $A(n)\equiv a\ \pmod {q}$
,
$A(n)\equiv a\ \pmod {q}$
,
![]() $P(n)$
begins with the digits of D in base b, and
$P(n)$
begins with the digits of D in base b, and
![]() $P(n) \in (x^{1/U'},y]$
is
$P(n) \in (x^{1/U'},y]$
is
 $$\begin{align*}\frac{1}{q}\frac{\log(1+D^{-1})}{\log{b}}\left(\rho(u)-\rho(U')\right)x + o(x/q), \end{align*}$$
$$\begin{align*}\frac{1}{q}\frac{\log(1+D^{-1})}{\log{b}}\left(\rho(u)-\rho(U')\right)x + o(x/q), \end{align*}$$
where
![]() $u:=\frac {\log {x}}{\log {y}}$
, where
$u:=\frac {\log {x}}{\log {y}}$
, where
![]() $x,y\to \infty $
with
$x,y\to \infty $
with
![]() $y\ge x^{1/U}$
, and where
$y\ge x^{1/U}$
, and where
![]() $a\bmod {q}$
is any residue class with
$a\bmod {q}$
is any residue class with
![]() $q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
$q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
Proof (sketch)
The proof is similar to the case
![]() $k=1$
of Proposition 2.2, with the needed input on
$k=1$
of Proposition 2.2, with the needed input on
![]() $\Psi (x,y)$
replaced by appeals to Lemma 3.3. We may assume
$\Psi (x,y)$
replaced by appeals to Lemma 3.3. We may assume
![]() $y = x^{1/u}$
where
$y = x^{1/u}$
where
![]() $u\ge 1$
is fixed. With the intervals
$u\ge 1$
is fixed. With the intervals
![]() $\mathcal {I}_j$
defined as in (2.4), the desired count of n is given by the triple sum
$\mathcal {I}_j$
defined as in (2.4), the desired count of n is given by the triple sum
 $$ \begin{align} \sum_{j\ge 0} \sum_{p \in \mathcal{I}_j \cap (x^{1/U'},y]} \sum_{\substack{n \le x\\P(n)=p \\ A(n)\equiv a\ \pmod{q}}} 1.\end{align} $$
$$ \begin{align} \sum_{j\ge 0} \sum_{p \in \mathcal{I}_j \cap (x^{1/U'},y]} \sum_{\substack{n \le x\\P(n)=p \\ A(n)\equiv a\ \pmod{q}}} 1.\end{align} $$
At the cost of a negligible error, we may restrict the outer sum to
![]() $j \in \mathcal {J}$
, where
$j \in \mathcal {J}$
, where
![]() $\mathcal {J}$
is the collection of nonnegative integers j with
$\mathcal {J}$
is the collection of nonnegative integers j with
![]() $\mathcal {I}_j \subset (x^{1/U'}, y/\exp (\sqrt {\log {x}}))$
; indeed, defining (as before)
$\mathcal {I}_j \subset (x^{1/U'}, y/\exp (\sqrt {\log {x}}))$
; indeed, defining (as before)
![]() $P:=(x^{1/U'}, bx^{1/U'}]$
and
$P:=(x^{1/U'}, bx^{1/U'}]$
and
![]() $P':=[y/b\exp (\sqrt {\log {x}}), y]$
, the incurred error is of size
$P':=[y/b\exp (\sqrt {\log {x}}), y]$
, the incurred error is of size
which is
![]() $o(x/q)$
. Now, suppose
$o(x/q)$
. Now, suppose
![]() $j \in \mathcal {J}$
and
$j \in \mathcal {J}$
and
![]() $p \in \mathcal {I}_j$
; then, by Lemma 3.3,
$p \in \mathcal {I}_j$
; then, by Lemma 3.3,
 $$\begin{align*}\sum_{\substack{n \le x\\P(n)=p \\ A(n)\equiv a\ \ \ \pmod{q}}} 1 = \sum_{\substack{m \le x/p \\ P(m) \le p \\ A(m)\equiv a-p\ \ \ \pmod{q}}} 1 = \frac{1}{q}\Psi(x/p,p) + O\left(\frac{x}{p(\log{(x/p)})^{\frac{1}{2}(1-\epsilon)}}\right).\end{align*}$$
$$\begin{align*}\sum_{\substack{n \le x\\P(n)=p \\ A(n)\equiv a\ \ \ \pmod{q}}} 1 = \sum_{\substack{m \le x/p \\ P(m) \le p \\ A(m)\equiv a-p\ \ \ \pmod{q}}} 1 = \frac{1}{q}\Psi(x/p,p) + O\left(\frac{x}{p(\log{(x/p)})^{\frac{1}{2}(1-\epsilon)}}\right).\end{align*}$$
Summing on all
![]() $j \in \mathcal {J}$
and all
$j \in \mathcal {J}$
and all
![]() $p \in \mathcal {I}_j$
, the contribution from O-terms is
$p \in \mathcal {I}_j$
, the contribution from O-terms is
 $$\begin{align*}\ll x \sum_{x^{1/U'} < p \le x/2} \frac{1}{p(\log{(x/p)})^{\frac{1}{2}(1-\epsilon)}} \ll \frac{x}{(\log{x})^{\frac{1}{2}(1-\epsilon)}}, \end{align*}$$
$$\begin{align*}\ll x \sum_{x^{1/U'} < p \le x/2} \frac{1}{p(\log{(x/p)})^{\frac{1}{2}(1-\epsilon)}} \ll \frac{x}{(\log{x})^{\frac{1}{2}(1-\epsilon)}}, \end{align*}$$
which is
![]() $o(x/q)$
. (Perhaps the simplest way to estimate this last sum on p is to consider, for each j, the contribution from p with
$o(x/q)$
. (Perhaps the simplest way to estimate this last sum on p is to consider, for each j, the contribution from p with
![]() $x/p \in (e^j,e^{j+1}]$
.) On the other hand, the calculations from the proof of Proposition 2.2 (with
$x/p \in (e^j,e^{j+1}]$
.) On the other hand, the calculations from the proof of Proposition 2.2 (with
![]() $k=1$
,
$k=1$
,
![]() $q=1$
) already show that
$q=1$
) already show that
 $$\begin{align*}\sum_{j \in \mathcal{J}} \sum_{p \in \mathcal{I}_j} \Psi(x/p,p) = \frac{\log(1+D^{-1})}{\log{b}} (\rho(u)-\rho(U')+o(1))x. \end{align*}$$
$$\begin{align*}\sum_{j \in \mathcal{J}} \sum_{p \in \mathcal{I}_j} \Psi(x/p,p) = \frac{\log(1+D^{-1})}{\log{b}} (\rho(u)-\rho(U')+o(1))x. \end{align*}$$
Collecting estimates, we deduce that (3.5) is
![]() $\frac {1}{q}\frac {\log (1+D^{-1})}{\log {b}}\left (\rho (u)-\rho (U')\right )x + o(x/q)$
, as desired.
$\frac {1}{q}\frac {\log (1+D^{-1})}{\log {b}}\left (\rho (u)-\rho (U')\right )x + o(x/q)$
, as desired.
Proposition 3.4 implies the following variant of Theorem 1.2, with the leading digits of
![]() $P(n)$
prescribed (instead of those of
$P(n)$
prescribed (instead of those of
![]() $A(n)$
).
$A(n)$
).
Proposition 3.5 Fix positive integers
![]() $k,D$
, and b with
$k,D$
, and b with
![]() $b\ge 2$
. Fix a real number
$b\ge 2$
. Fix a real number
![]() $U \ge 1$
, and fix
$U \ge 1$
, and fix
![]() $\epsilon> 0$
. The number of
$\epsilon> 0$
. The number of
![]() $n\le x$
for which
$n\le x$
for which
![]() $A(n)\equiv a\ \pmod {q}$
,
$A(n)\equiv a\ \pmod {q}$
,
![]() $P(n)$
begins with the digits of D in base b, and
$P(n)$
begins with the digits of D in base b, and
![]() $P(n) \le y$
is
$P(n) \le y$
is
 $$\begin{align*}\sim \frac{1}{q}\frac{\log(1+D^{-1})}{\log{b}} \Psi(x,y), \end{align*}$$
$$\begin{align*}\sim \frac{1}{q}\frac{\log(1+D^{-1})}{\log{b}} \Psi(x,y), \end{align*}$$
where
![]() $x,y\to \infty $
with
$x,y\to \infty $
with
![]() $y\ge x^{1/U}$
, and where
$y\ge x^{1/U}$
, and where
![]() $a\bmod {q}$
is any residue class with
$a\bmod {q}$
is any residue class with
![]() $q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
$q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
Proof The proof parallels that of Theorem 1.1. It suffices to show that the count of n in question is eventually larger than
![]() $\frac {1}{q} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho (u)-\eta \right )x$
and eventually smaller than
$\frac {1}{q} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho (u)-\eta \right )x$
and eventually smaller than
![]() $\frac {1}{q} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho (u)+\eta \right )x$
. The lower bound follows from Proposition 3.4, fixing
$\frac {1}{q} \frac {\log (1+D^{-1})}{\log {b}} \left (\rho (u)+\eta \right )x$
. The lower bound follows from Proposition 3.4, fixing
![]() $U'$
large enough that
$U'$
large enough that
![]() $\rho (U') < \eta $
. For the upper bound, we fix
$\rho (U') < \eta $
. For the upper bound, we fix
![]() $U'$
large enough that
$U'$
large enough that
![]() $\rho (U') < \eta \frac {\log (1+D^{-1})}{\log {b}}$
; the upper bound inequality then follows from Lemma 3.3 and Proposition 3.4.
$\rho (U') < \eta \frac {\log (1+D^{-1})}{\log {b}}$
; the upper bound inequality then follows from Lemma 3.3 and Proposition 3.4.
To finish the proof of Theorem 1.2, we show that
![]() $P(n)$
and
$P(n)$
and
![]() $A(n)$
usually have the same leading digits. We begin by observing that
$A(n)$
usually have the same leading digits. We begin by observing that
![]() $P(n)$
and
$P(n)$
and
![]() $A(n)$
are usually close.
$A(n)$
are usually close.
Lemma 3.6 Fix
![]() $\delta> 0$
. For large x, the number of
$\delta> 0$
. For large x, the number of
![]() $n\le x$
for which
$n\le x$
for which
![]() $A(n)> (1+\delta ) P(n)$
is
$A(n)> (1+\delta ) P(n)$
is
![]() $O(x (\log \log {x})^2/\log {x})$
.
$O(x (\log \log {x})^2/\log {x})$
.
Proof Put
![]() $y:= x^{1/2\log \log {x}}$
. We may suppose that
$y:= x^{1/2\log \log {x}}$
. We may suppose that
![]() $P(n)> y$
, since by standard results on the distribution of smooth numbers (e.g., Theorem 5.1 on page 512 of [Reference Tenenbaum26]) this condition excludes only
$P(n)> y$
, since by standard results on the distribution of smooth numbers (e.g., Theorem 5.1 on page 512 of [Reference Tenenbaum26]) this condition excludes only
![]() $O(x/\log {x})$
integers
$O(x/\log {x})$
integers
![]() $n\le x$
. If
$n\le x$
. If
![]() $A(n)> (1+\delta )P(n)$
for one of these remaining n, then
$A(n)> (1+\delta )P(n)$
for one of these remaining n, then
![]() $\delta P(n) < \sum _{k>1} P_k(n) \le \Omega (n) P_2(n) \le 2 P_2(n) \log {x}$
. Hence, n is divisible by
$\delta P(n) < \sum _{k>1} P_k(n) \le \Omega (n) P_2(n) \le 2 P_2(n) \log {x}$
. Hence, n is divisible by
![]() $pp'$
for primes
$pp'$
for primes
![]() $p, p'$
with
$p, p'$
with
![]() $p> y$
and
$p> y$
and
![]() $p' \in (\frac {\delta }{2} p/\log {x},p]$
. The number of such
$p' \in (\frac {\delta }{2} p/\log {x},p]$
. The number of such
![]() $n\le x$
is
$n\le x$
is
 $$\begin{align*}x \sum_{y<p\le x}\sum_{\frac{\delta}{2} \frac{p}{\log{x}}<p'\le p}\frac{1}{pp'} \ll x\sum_{y<p\le x} \frac{1}{p} \frac{\log\log{x}}{\log{p}} \ll x\frac{\log\log{x}}{\log{y}} \ll x \frac{(\log\log{x})^2}{\log{x}}. \end{align*}$$
$$\begin{align*}x \sum_{y<p\le x}\sum_{\frac{\delta}{2} \frac{p}{\log{x}}<p'\le p}\frac{1}{pp'} \ll x\sum_{y<p\le x} \frac{1}{p} \frac{\log\log{x}}{\log{p}} \ll x\frac{\log\log{x}}{\log{y}} \ll x \frac{(\log\log{x})^2}{\log{x}}. \end{align*}$$
Here, the sum on
![]() $p'$
has been estimated using Mertens’ theorem with the usual
$p'$
has been estimated using Mertens’ theorem with the usual
![]() $1/\log $
error term [Reference Tenenbaum26, Theorem 1.10, p. 18].
$1/\log $
error term [Reference Tenenbaum26, Theorem 1.10, p. 18].
Lemma 3.7 Fix positive integers N and b, with
![]() $b\ge 2$
, and fix a real number
$b\ge 2$
, and fix a real number
![]() $\epsilon> 0$
. Among all
$\epsilon> 0$
. Among all
![]() $n\le x$
with
$n\le x$
with
![]() $A(n)\equiv a\ \pmod {q}$
, the number of n for which the N leading base b digits of
$A(n)\equiv a\ \pmod {q}$
, the number of n for which the N leading base b digits of
![]() $P(n)$
do not coincide with those of
$P(n)$
do not coincide with those of
![]() $A(n)$
is
$A(n)$
is
![]() $o(x/q)$
, as
$o(x/q)$
, as
![]() $x\to \infty $
, uniformly in residue classes
$x\to \infty $
, uniformly in residue classes
![]() $a\bmod {q}$
with
$a\bmod {q}$
with
![]() $q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
$q\le (\log {x})^{\frac {1}{2}-\epsilon }$
.
Proof Since b and N are fixed, it is enough to prove the estimate of the lemma under the assumption that the N leading digits in the base b expansion of
![]() $P(n)$
are fixed, say as the digits of the positive integer D.
$P(n)$
are fixed, say as the digits of the positive integer D.
For M a (fixed) positive integer to be specified momentarily, we let
![]() $D'$
be the integer obtained by tacking M copies of the digit “
$D'$
be the integer obtained by tacking M copies of the digit “
![]() $b-1$
” on to the end of the b-ary expansion of D. Thus,
$b-1$
” on to the end of the b-ary expansion of D. Thus,
![]() $D' = b^M D + (b^M-1)$
.
$D' = b^M D + (b^M-1)$
.
Suppose
![]() $P(n)$
begins with D in base b, but
$P(n)$
begins with D in base b, but
![]() $A(n)$
does not. We take two cases. First, it may be that
$A(n)$
does not. We take two cases. First, it may be that
![]() $P(n)$
begins with D but not
$P(n)$
begins with D but not
![]() $D'$
; in that case, for
$D'$
; in that case, for
![]() $A(n)$
to not begin with D, we must have
$A(n)$
to not begin with D, we must have
![]() $A(n)/P(n)> 1+1/D'$
. By Lemma 3.6, the number of such
$A(n)/P(n)> 1+1/D'$
. By Lemma 3.6, the number of such
![]() $n\le x$
is
$n\le x$
is
![]() $O(x(\log \log {x})^2/\log {x})$
, which is
$O(x(\log \log {x})^2/\log {x})$
, which is
![]() $o(x/q)$
. On the other hand, if
$o(x/q)$
. On the other hand, if
![]() $P(n)$
begins with
$P(n)$
begins with
![]() $D'$
, we apply Proposition 3.5. Taking
$D'$
, we apply Proposition 3.5. Taking
![]() $y=x$
there, we see that the number of
$y=x$
there, we see that the number of
![]() $n\le x$
for which
$n\le x$
for which
![]() $P(n)$
begins with
$P(n)$
begins with
![]() $D'$
and
$D'$
and
![]() $A(n)\equiv a\ \pmod {q}$
is
$A(n)\equiv a\ \pmod {q}$
is
![]() $\sim \frac {\log (1+1/D')}{\log {b}}\frac {x}{q}$
. Since the coefficient
$\sim \frac {\log (1+1/D')}{\log {b}}\frac {x}{q}$
. Since the coefficient
![]() $\frac {\log (1+1/D')}{\log {b}}$
of
$\frac {\log (1+1/D')}{\log {b}}$
of
![]() $\frac {x}{q}$
in this estimate can be made as small as we like by fixing M large enough, we obtain the lemma.
$\frac {x}{q}$
in this estimate can be made as small as we like by fixing M large enough, we obtain the lemma.
Theorem 1.2 follows from combining Proposition 3.5 with Lemma 3.7.
Remark The range of uniformity in q can be widened under the assumption that q is supported on sufficiently large primes. More precisely, for any fixed
![]() $Q \ge 2$
, the result of Theorem 1.2 holds uniformly for
$Q \ge 2$
, the result of Theorem 1.2 holds uniformly for
![]() $q \leq (\log x)^{1-1/Q-\epsilon }$
, provided the least prime
$q \leq (\log x)^{1-1/Q-\epsilon }$
, provided the least prime
![]() $P^-(q)$
dividing q is at least
$P^-(q)$
dividing q is at least
![]() $Q+1$
. The key observation is that, in the notation of Lemma 3.3, such q have
$Q+1$
. The key observation is that, in the notation of Lemma 3.3, such q have
![]() $\phi (q') \ge P^-(q)-1 \ge Q$
, which shows that
$\phi (q') \ge P^-(q)-1 \ge Q$
, which shows that
 $$\begin{align*}\frac{\pi(\mathcal{I})}{\phi(q') u} (\phi(q') - \mathop{\mathrm{Re}}(\mu(q') u^{-it})) \ge \left(1-\frac1Q\right) \frac{\pi(\mathcal{I})}{u}\end{align*}$$
$$\begin{align*}\frac{\pi(\mathcal{I})}{\phi(q') u} (\phi(q') - \mathop{\mathrm{Re}}(\mu(q') u^{-it})) \ge \left(1-\frac1Q\right) \frac{\pi(\mathcal{I})}{u}\end{align*}$$
in the display (3.4). The remainder of the proof requires only minor modifications.
Acknowledgment
We thank the referees for their careful reading of the manuscript.