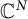1 Introduction
Our goal is to completely characterize which linear fractional transformations map the ball
![]() $\mathbb {B}^N$
into itself for
$\mathbb {B}^N$
into itself for
![]() $N>1$
. We recall the unit ball is defined as
$N>1$
. We recall the unit ball is defined as
A characterization for
![]() $N=1$
can be determined by noting that linear fractional maps (LFMs) in the disk map the boundary of the disk to a dilated and translated automorphism of the disk. This determination makes critical use of the well-known fact that LFMs map generalized circles to generalized circles, where a generalized circle is defined to include lines. This unique feature of LFMs will prevent our results in this article from generalizing to rational maps of degree greater than
$N=1$
can be determined by noting that linear fractional maps (LFMs) in the disk map the boundary of the disk to a dilated and translated automorphism of the disk. This determination makes critical use of the well-known fact that LFMs map generalized circles to generalized circles, where a generalized circle is defined to include lines. This unique feature of LFMs will prevent our results in this article from generalizing to rational maps of degree greater than
![]() $1$
.
$1$
.
In order to replicate this line of reasoning in higher dimensions, we first produce some preliminary results about LFMs.
2 LFMs in
 $\mathbb {C}^N$
$\mathbb {C}^N$
Recall that a LFM in
![]() $\mathbb {C}$
is defined as
$\mathbb {C}$
is defined as
where the coefficients a, b, c, and d are complex numbers such that
![]() $ad-bc \neq 0$
(otherwise,
$ad-bc \neq 0$
(otherwise,
![]() $\phi (z)$
is a constant function).
$\phi (z)$
is a constant function).
Given such a map
![]() $\phi $
, we will find it insightful to make use of its associated matrix, defined as
$\phi $
, we will find it insightful to make use of its associated matrix, defined as
 $$ \begin{align*} m_{\phi} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align*} $$
$$ \begin{align*} m_{\phi} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align*} $$
For
![]() $c \neq 0$
, we must have
$c \neq 0$
, we must have
![]() $z \neq -\frac {d}{c}$
, from which it follows, in order to avoid poles in the disk, that the inequality
$z \neq -\frac {d}{c}$
, from which it follows, in order to avoid poles in the disk, that the inequality
must hold. While this is a necessary condition for a LFM to be a self-map of the disk, it is not sufficient. It turns out a stronger condition holds.
Theorem 2.1 The LFM
![]() $\phi (z)=\frac {az+b}{cz+d}$
is a self-map of the disk if and only if the following inequality holds:
$\phi (z)=\frac {az+b}{cz+d}$
is a self-map of the disk if and only if the following inequality holds:
It appears the most accessible location of the proof, which is relatively simple, can be found in Martín’s paper [Reference Martín7]. Another location of the proof can be found in [Reference Hinkkanen5]. Other than this, it seem to have primarily resided in the mathematical folklore.
We aim to obtain a parallel result in
![]() $\mathbb {B}^N$
for
$\mathbb {B}^N$
for
![]() $N>1$
. In order to discuss linear fractional self-maps in higher dimensions, we must first state what it means to be a LFM in
$N>1$
. In order to discuss linear fractional self-maps in higher dimensions, we must first state what it means to be a LFM in
![]() $\mathbb {C}^N$
. One remarkable fact about LFMs in
$\mathbb {C}^N$
. One remarkable fact about LFMs in
![]() $\mathbb {C}$
is that they are exactly the linear transformations in homogeneous coordinates. Taking the perspective that LFMs in
$\mathbb {C}$
is that they are exactly the linear transformations in homogeneous coordinates. Taking the perspective that LFMs in
![]() $\mathbb {C}^N$
should share this property, we arrive at the following definition. For more details, see [Reference Pilla8].
$\mathbb {C}^N$
should share this property, we arrive at the following definition. For more details, see [Reference Pilla8].
Definition 2.1 We say
![]() $\phi $
is a LFM in
$\phi $
is a LFM in
![]() $\mathbb {C}^N$
if
$\mathbb {C}^N$
if
where A is an
![]() $N \times N$
matrix, B and C are column vectors in
$N \times N$
matrix, B and C are column vectors in
![]() $\mathbb {C}^N$
,
$\mathbb {C}^N$
,
![]() $D \in \mathbb {C}$
, and
$D \in \mathbb {C}$
, and
![]() $\langle \cdot , \cdot \rangle $
is the standard inner product.
$\langle \cdot , \cdot \rangle $
is the standard inner product.
As in the case of the disk, the domain of
![]() $\phi $
is given by
$\phi $
is given by
![]() $\{z \in \mathbb {C}^N \mid \langle z, C \rangle +D \neq 0\}$
. In order to avoid poles in the unit ball, we then require
$\{z \in \mathbb {C}^N \mid \langle z, C \rangle +D \neq 0\}$
. In order to avoid poles in the unit ball, we then require
![]() $|D|^2>|C|^2$
since
$|D|^2>|C|^2$
since
![]() $z=-\frac {DC}{|C|^2}$
is a zero of
$z=-\frac {DC}{|C|^2}$
is a zero of
![]() $\langle z, C \rangle +D$
which for our case requires
$\langle z, C \rangle +D$
which for our case requires
![]() $\left |-\frac {DC}{|C|^2}\right |>1$
.
$\left |-\frac {DC}{|C|^2}\right |>1$
.
We define the associated matrix
![]() $m_{\phi }$
of the LFM
$m_{\phi }$
of the LFM
![]() $\phi (z)=\frac {Az+B}{\langle z,C\rangle +D}$
to be given by
$\phi (z)=\frac {Az+B}{\langle z,C\rangle +D}$
to be given by
 $$ \begin{align*} m_{\phi} = \begin{pmatrix} A & B \\ C^* & D \end{pmatrix}. \end{align*} $$
$$ \begin{align*} m_{\phi} = \begin{pmatrix} A & B \\ C^* & D \end{pmatrix}. \end{align*} $$
Note that for a LFM in
![]() $\mathbb {C}^N$
,
$\mathbb {C}^N$
,
![]() $m_{\phi }$
will be an
$m_{\phi }$
will be an
![]() $(n+1) \times (n+1)$
matrix. For LFMs
$(n+1) \times (n+1)$
matrix. For LFMs
![]() $\phi $
and
$\phi $
and
![]() $\psi $
, a routine calculation shows that
$\psi $
, a routine calculation shows that
![]() $m_{\phi \circ \psi }=m_{\phi }m_{\psi }$
and
$m_{\phi \circ \psi }=m_{\phi }m_{\psi }$
and
![]() $m_{\phi ^{-1}}=(m_{\phi })^{-1}$
. Thus, function composition corresponds to matrix multiplication and
$m_{\phi ^{-1}}=(m_{\phi })^{-1}$
. Thus, function composition corresponds to matrix multiplication and
![]() $m_{\phi }$
is invertible as a matrix if and only if the LFM
$m_{\phi }$
is invertible as a matrix if and only if the LFM
![]() $\phi $
has an inverse. In order to ensure this, we will presume
$\phi $
has an inverse. In order to ensure this, we will presume
![]() $\phi $
is one-to-one.
$\phi $
is one-to-one.
In order to generalize the results of Martín, we ask if our LFMs map generalized spheres to generalized spheres in
![]() $\mathbb {C}^N$
for
$\mathbb {C}^N$
for
![]() $N>1$
. It turns out this is just a little too much to ask. We do, however, have the following.
$N>1$
. It turns out this is just a little too much to ask. We do, however, have the following.
Theorem 2.2 LFMs in
![]() $\mathbb {C}^N$
map generalized ellipsoids to generalized ellipsoids.
$\mathbb {C}^N$
map generalized ellipsoids to generalized ellipsoids.
For LFMs defined on the closed unit ball, this results was proved by Cowen and MacCluer [Reference Cowen and MacCluer3]. For this result, a generalized ellipsoid is defined as the image of
![]() $\mathbb {B}^N$
under an invertible linear transformation composed with a translation.
$\mathbb {B}^N$
under an invertible linear transformation composed with a translation.
We aim to discuss these objects in a more tractable way, demonstrating a novel proof of the ellipsoid-preserving properties of LFMs, more reminiscent of the proof in one complex variable. In order to do so, however, we first investigate how to decompose LFMs into their atomic parts.
3 Decomposition of linear fractional maps
Our goal in this section will be to decompose LFMs into a canon of simpler maps. In one variable, one obtains a rather nice decomposition through some clever rewriting. The simplest way to generalize this result is to appeal to decomposition of the associated matrix. Given an invertible matrix
![]() $m_{\phi }$
associated with a LFM
$m_{\phi }$
associated with a LFM
![]() $\phi $
, Bruhat decomposition tells us we may write
$\phi $
, Bruhat decomposition tells us we may write
![]() $m_{\phi }$
as a (matrix) product of the following: permutation matrices, upper triangular unipotent matrices, and diagonal matrices. Here, unipotent means each diagonal entry is
$m_{\phi }$
as a (matrix) product of the following: permutation matrices, upper triangular unipotent matrices, and diagonal matrices. Here, unipotent means each diagonal entry is
![]() $1$
. See, for example, [Reference Humphreys4] for more details.
$1$
. See, for example, [Reference Humphreys4] for more details.
Permutation matrices may be further decomposed into a product of matrices that permute two of the variables and leave the others fixed. The associated LFMs play the analog of inversion maps in one variable. In hindsight, perhaps this is what ought to be expected. If one takes the perspective that, in the complex plane, inversion is simply reflection about the boundary of the disk, then inversion analogs in higher dimensions manifesting themselves as reflections permuting two variables is not so surprising. This motivates the following definition.
Definition 3.1 A LFM from
![]() $\mathbb {C}^N$
to
$\mathbb {C}^N$
to
![]() $\mathbb {C}^N$
will be called a reflection if its associated matrix is a permutation matrix that permutes precisely two variables and fixes the rest.
$\mathbb {C}^N$
will be called a reflection if its associated matrix is a permutation matrix that permutes precisely two variables and fixes the rest.
These inversion analogs also draw attention to some of the stark differences in higher dimensions. In
![]() $\mathbb {C}$
, the map
$\mathbb {C}$
, the map
![]() $\frac {1}{z}$
possesses several useful properties, including the fact that it inverts the unit disk while mapping its boundary onto itself. The author shouldn’t need to do much convincing to remind the reader of the countless results in complex analysis that utilize this fact. Thus, it is worth understanding the nature of its analogs in several variables.
$\frac {1}{z}$
possesses several useful properties, including the fact that it inverts the unit disk while mapping its boundary onto itself. The author shouldn’t need to do much convincing to remind the reader of the countless results in complex analysis that utilize this fact. Thus, it is worth understanding the nature of its analogs in several variables.
This also draws attention to the fact that we are making a conscious decision to first investigate self-maps of the unit ball. The study of one complex variable bifurcates into the study of
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathbb {D}$
since all other simply-connected open subsets of
$\mathbb {D}$
since all other simply-connected open subsets of
![]() $\mathbb {C}$
are biholomorphically equivalent to
$\mathbb {C}$
are biholomorphically equivalent to
![]() $\mathbb {D}$
by the Riemann Mapping Theorem. It’s well-known that this theorem fails spectacularly even in
$\mathbb {D}$
by the Riemann Mapping Theorem. It’s well-known that this theorem fails spectacularly even in
![]() $\mathbb {C}^2$
. In fact, even the unit polydisk, defined by
$\mathbb {C}^2$
. In fact, even the unit polydisk, defined by
is not biholomorphically equivalent to the unit ball
![]() $\mathbb {B}^N$
for
$\mathbb {B}^N$
for
![]() $N>1$
. With this in mind, it is interesting to note that our reflections do map the boundary of the polydisk into itself. One may also conclude by our decomposition that inversion of
$N>1$
. With this in mind, it is interesting to note that our reflections do map the boundary of the polydisk into itself. One may also conclude by our decomposition that inversion of
![]() $\mathbb {B}^N$
by a LFM is unique to the case
$\mathbb {B}^N$
by a LFM is unique to the case
![]() $N=1$
.
$N=1$
.
To handle the upper triangular matrices, we make the following definition.
Definition 3.2 A LFM from
![]() $\mathbb {C}^N$
to
$\mathbb {C}^N$
to
![]() $\mathbb {C}^N$
will be called a multi-linear map if it can be written in the form
$\mathbb {C}^N$
will be called a multi-linear map if it can be written in the form
![]() $\left (\langle z, \alpha _1 \rangle +c_1, \langle z, \alpha _2 \rangle +c_2, \ldots, \langle z,\alpha_N \rangle + c_N \right )$
for some vectors
$\left (\langle z, \alpha _1 \rangle +c_1, \langle z, \alpha _2 \rangle +c_2, \ldots, \langle z,\alpha_N \rangle + c_N \right )$
for some vectors
![]() $\{\alpha_k\}_{k=1}^{N} $
and constants
$\{\alpha_k\}_{k=1}^{N} $
and constants
![]() $\{c_k\}_{k=1}^{N}$
.
$\{c_k\}_{k=1}^{N}$
.
The below theorem then quickly follows from the Bruhat decomposition of the associated matrix of the LFM.
Theorem 3.1 Any LFM in
![]() $\mathbb {C}^N$
can be written as a composition of multi-linear maps and reflections.
$\mathbb {C}^N$
can be written as a composition of multi-linear maps and reflections.
4 Generalized ellipsoids
Now that we have decomposed our LFMs, we may proceed to our desired result. It suffices to show our results for reflections and multi-linear maps.
Theorem 4.1 Let
![]() $\phi $
be a LFM in
$\phi $
be a LFM in
![]() $\mathbb {B}^N$
. Then
$\mathbb {B}^N$
. Then
![]() $\phi $
maps generalized ellipsoids to generalized ellipsoids.
$\phi $
maps generalized ellipsoids to generalized ellipsoids.
Proof We first show it is true for reflections. It suffices to show that the map
maps generalized ellipsoids to generalized ellipsoids. Recalling that a generalized ellipsoid is defined as the image of the unit ball under a linear transformation and translation, without loss of generality, it is clear to see that one may write a generalized ellipsoid in standard form as
 $$ \begin{align*} \sum_{i=1}^N \alpha_i |z_i|^2+\sum_{i=1}^N\beta_i \Re(z_i)+\sum_{i=1}^N \gamma_i \Im(z_i)+\delta=0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^N \alpha_i |z_i|^2+\sum_{i=1}^N\beta_i \Re(z_i)+\sum_{i=1}^N \gamma_i \Im(z_i)+\delta=0. \end{align*} $$
Noting that
![]() $\frac {1}{z_N}=\frac {\overline {z_N}}{|z_N|^2}$
, we have
$\frac {1}{z_N}=\frac {\overline {z_N}}{|z_N|^2}$
, we have
 $$ \begin{align*} &=\sum_{i=1}^{N-1} \alpha_i \left|\frac{z_i}{z_N}\right|^2+\alpha_N\left|\frac{1}{z_N}\right|^2+\sum_{i=1}^{N-1}\beta_i \Re\left(\frac{z_i\overline{z_N}}{|z_N|^2}\right)+\beta_N \Re\left(\frac{\overline{z_N}}{|z_N|^2}\right)\\ &+\sum_{i=1}^{N-1}\gamma_i \Im\left(\frac{z_i\overline{z_N}}{|z_N|^2}\right)+\gamma_N \Im\left(\frac{\overline{z_N}}{|z_N|^2}\right)+\delta=0, \end{align*} $$
$$ \begin{align*} &=\sum_{i=1}^{N-1} \alpha_i \left|\frac{z_i}{z_N}\right|^2+\alpha_N\left|\frac{1}{z_N}\right|^2+\sum_{i=1}^{N-1}\beta_i \Re\left(\frac{z_i\overline{z_N}}{|z_N|^2}\right)+\beta_N \Re\left(\frac{\overline{z_N}}{|z_N|^2}\right)\\ &+\sum_{i=1}^{N-1}\gamma_i \Im\left(\frac{z_i\overline{z_N}}{|z_N|^2}\right)+\gamma_N \Im\left(\frac{\overline{z_N}}{|z_N|^2}\right)+\delta=0, \end{align*} $$
which simplifies to
 $$ \begin{align*} &\sum_{i=1}^{N-1} \alpha_i \left|z_i\right|^2+\alpha_N+\sum_{i=1}^{N-1}\beta_i \Re\left(z_i\overline{z_N}\right)+\beta_N \Re\left(\overline{z_N}\right)\\ &+\sum_{i=1}^{N-1}\gamma_i \Im\left(z_i\overline{z_N}\right)+\gamma_N \Im\left(\overline{z_N}\right)+\delta|z_N|^2=0, \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{N-1} \alpha_i \left|z_i\right|^2+\alpha_N+\sum_{i=1}^{N-1}\beta_i \Re\left(z_i\overline{z_N}\right)+\beta_N \Re\left(\overline{z_N}\right)\\ &+\sum_{i=1}^{N-1}\gamma_i \Im\left(z_i\overline{z_N}\right)+\gamma_N \Im\left(\overline{z_N}\right)+\delta|z_N|^2=0, \end{align*} $$
which simplifies to
 $$ \begin{align*} &=\sum_{i=1}^{N-1} \alpha_i \left|z_i\right|^2+\alpha_N+\sum_{i=1}^{N-1}\beta_i \Re(z_i)\Re(z_N)+\sum_{i=1}^{N-1}\beta_i \Im(z_i)\Im(z_N)\\ &+\beta_N \Re\left(z_N\right)+\sum_{i=1}^{N-1}\gamma_i \Re(z_i)\Im(z_N)-\sum_{i=1}^{N-1}\gamma_i \Im(z_i)\Re(z_N)\\ &-\gamma_N \Im\left(z_N\right)+\delta|z_N|^2=0. \end{align*} $$
$$ \begin{align*} &=\sum_{i=1}^{N-1} \alpha_i \left|z_i\right|^2+\alpha_N+\sum_{i=1}^{N-1}\beta_i \Re(z_i)\Re(z_N)+\sum_{i=1}^{N-1}\beta_i \Im(z_i)\Im(z_N)\\ &+\beta_N \Re\left(z_N\right)+\sum_{i=1}^{N-1}\gamma_i \Re(z_i)\Im(z_N)-\sum_{i=1}^{N-1}\gamma_i \Im(z_i)\Re(z_N)\\ &-\gamma_N \Im\left(z_N\right)+\delta|z_N|^2=0. \end{align*} $$
We next note that this is an equation of a generalized ellipsoid in nonstandard form.
Next, we consider multi-linear maps. Letting
![]() $z_k=x_k+iy_k$
,
$z_k=x_k+iy_k$
,
![]() $\alpha _{ij}=u_{jk}+iv_{jk}$
, and
$\alpha _{ij}=u_{jk}+iv_{jk}$
, and
![]() $\beta _{j}=s_j+it_j$
, we have
$\beta _{j}=s_j+it_j$
, we have
 $$ \begin{align*} &\sum_{j=1}^N \left|\beta_i+\sum_{k=1}^N\alpha_{jk}z_k\right|^2=\sum_{j=1}^N \left|s_j+\sum_{k=1}^N \left(u_{jk}x_k-v_{jk}y_k\right)+i\left(t_j+\sum_{k=1}^N(v_{jk}x_k+u_{jk}y_k)\right)\right|^2\\ &=\sum_{j=1}^N\left[\left(s_j+\sum_{k=1}^N \left(u_{jk}x_k-v_{jk}y_k\right)\right)^2+\left(t_j+\sum_{k=1}^N(v_{jk}x_k+u_{jk}y_k)\right)^2\right]. \end{align*} $$
$$ \begin{align*} &\sum_{j=1}^N \left|\beta_i+\sum_{k=1}^N\alpha_{jk}z_k\right|^2=\sum_{j=1}^N \left|s_j+\sum_{k=1}^N \left(u_{jk}x_k-v_{jk}y_k\right)+i\left(t_j+\sum_{k=1}^N(v_{jk}x_k+u_{jk}y_k)\right)\right|^2\\ &=\sum_{j=1}^N\left[\left(s_j+\sum_{k=1}^N \left(u_{jk}x_k-v_{jk}y_k\right)\right)^2+\left(t_j+\sum_{k=1}^N(v_{jk}x_k+u_{jk}y_k)\right)^2\right]. \end{align*} $$
From which it is evident, after expansion, that we will have the form of a generalized ellipsoid in nonstandard form.
5 Automorphisms of
 $\mathbb {B}^N$
and
$\mathbb {B}^N$
and
 $\mathbb {D}^N$
$\mathbb {D}^N$
Recall that for
![]() $\alpha $
with
$\alpha $
with
![]() $|\alpha |<1$
, there is an automorphism of the disk
$|\alpha |<1$
, there is an automorphism of the disk
![]() $\phi _{\alpha }$
given by
$\phi _{\alpha }$
given by
such that
![]() $\phi _{\alpha }(0)=\alpha $
and
$\phi _{\alpha }(0)=\alpha $
and
![]() $\phi _{\alpha }(\alpha )=0$
.
$\phi _{\alpha }(\alpha )=0$
.
In fact, all automorphism of the disk can be written as
for some
![]() $\alpha $
in the disk. In particular, note that up to rotation, all automorphisms of the disk are LFMs. Furthermore, for
$\alpha $
in the disk. In particular, note that up to rotation, all automorphisms of the disk are LFMs. Furthermore, for
![]() $N=1$
, the polydisk and unit ball are equivalent.
$N=1$
, the polydisk and unit ball are equivalent.
One might hope for similar results to be true for
![]() $\mathbb {B}^N$
and
$\mathbb {B}^N$
and
![]() $\mathbb {D}^N$
when
$\mathbb {D}^N$
when
![]() $N>1$
. It turns out such hopes are realized, although the group of automorphisms are different for each.
$N>1$
. It turns out such hopes are realized, although the group of automorphisms are different for each.
In the polydisk
![]() $\mathbb {D}^N$
, the automorphisms consist of automorphisms of the disk such as those in equation (5.2), composed with permutations of the disks (see Rudin [Reference Rudin11]). Since the polydisk is already a Cartesian product of disks in the complex plane, this result is not so surprising.
$\mathbb {D}^N$
, the automorphisms consist of automorphisms of the disk such as those in equation (5.2), composed with permutations of the disks (see Rudin [Reference Rudin11]). Since the polydisk is already a Cartesian product of disks in the complex plane, this result is not so surprising.
Let
![]() $\langle \phantom {z} , \phantom {z} \rangle $
denote the standard inner product, and for
$\langle \phantom {z} , \phantom {z} \rangle $
denote the standard inner product, and for
![]() $\alpha \in \mathbb {B}^N$
, let
$\alpha \in \mathbb {B}^N$
, let
![]() $P_{\alpha }$
denote the orthogonal projection of
$P_{\alpha }$
denote the orthogonal projection of
![]() $\mathbb {C}^N$
onto the span of
$\mathbb {C}^N$
onto the span of
![]() $\alpha $
and
$\alpha $
and
![]() $Q_{\alpha }(z)=z-P_{\alpha }(z)$
denote the projection onto the orthogonal complement of the span of
$Q_{\alpha }(z)=z-P_{\alpha }(z)$
denote the projection onto the orthogonal complement of the span of
![]() $\alpha $
. Letting
$\alpha $
. Letting
![]() $P_0(z)=0$
, we have
$P_0(z)=0$
, we have
Next, let
![]() $s_{\alpha }=\sqrt {1-|\alpha |^2}$
. We define the following map:
$s_{\alpha }=\sqrt {1-|\alpha |^2}$
. We define the following map:
for
![]() $\alpha \in \mathbb {B}^N$
. Note that this map is an involution and exchanges the points
$\alpha \in \mathbb {B}^N$
. Note that this map is an involution and exchanges the points
![]() $0$
and
$0$
and
![]() $\alpha $
.
$\alpha $
.
One may show that all automorphisms of
![]() $\mathbb {B}^N$
are of the form
$\mathbb {B}^N$
are of the form
![]() $U\phi _{\alpha }$
, where U is an
$U\phi _{\alpha }$
, where U is an
![]() $n \times n$
unitary matrix (see Rudin [Reference Rudin12]). As in the disk, U can be seen as a rotation of the ball.
$n \times n$
unitary matrix (see Rudin [Reference Rudin12]). As in the disk, U can be seen as a rotation of the ball.
Although it would take us too far afield to discuss domains beyond the unit ball and polydisk, for completion, we state the following result due to Ahn, Byun, and Park [Reference Ahn, Byun and Park1]. It turns out, for Hartog-type domains over classical Hermitian symmetric spaces, the automorphisms consists simply of the classical Lie groups.
6 Linear fractional self-maps of
 $\mathbb {B}^N$
$\mathbb {B}^N$
Given a LFM
![]() $\phi (z)=\frac {Az+B}{\langle z, C \rangle +D}$
, the main goal of this section is to study the range of
$\phi (z)=\frac {Az+B}{\langle z, C \rangle +D}$
, the main goal of this section is to study the range of
![]() $\phi $
on the unit ball. While we are not the first to study this, we will be taking a novel approach.
$\phi $
on the unit ball. While we are not the first to study this, we will be taking a novel approach.
The first results in this direction were by Cowen and MacCluer [Reference Cowen and MacCluer3] who showed that a LFM is a self-map of the unit ball if and only if its associated matrix is a Krein contraction. For
![]() $z_1$
in
$z_1$
in
![]() $\mathbb {C}^N$
and
$\mathbb {C}^N$
and
![]() $z_2 \neq 0$
in
$z_2 \neq 0$
in
![]() $\mathbb {C}$
, we identify
$\mathbb {C}$
, we identify
![]() $z=(z_1, z_2)$
with
$z=(z_1, z_2)$
with
![]() $v=\frac {z_1}{z_2}$
. For
$v=\frac {z_1}{z_2}$
. For
![]() $v, w$
described in this way, define the Krein inner product by
$v, w$
described in this way, define the Krein inner product by
![]() $[v,w]=\langle Jv, w \rangle $
, where
$[v,w]=\langle Jv, w \rangle $
, where
![]() $\langle \phantom {z}, \phantom {z} \rangle $
denotes the standard inner product with
$\langle \phantom {z}, \phantom {z} \rangle $
denotes the standard inner product with
 $$ \begin{align*}J=\begin{pmatrix} I & 0 \\ 0 & -1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}J=\begin{pmatrix} I & 0 \\ 0 & -1 \end{pmatrix}.\end{align*} $$
Thus, a map
![]() $\phi $
is a self-map of
$\phi $
is a self-map of
![]() $\mathbb {B}^N$
if and only if
$\mathbb {B}^N$
if and only if
for some
![]() $t>0$
. Without a way to determine t, however, this result doesn’t give a practical way of determining whether a specified LFM is a self-map of the unit ball. Geometric characterizations were also given by Bisi and Bracci [Reference Bisi and Bracci2] but such characterizations are not so practical for determining whether a given LFM is a self-map of the ball.
$t>0$
. Without a way to determine t, however, this result doesn’t give a practical way of determining whether a specified LFM is a self-map of the unit ball. Geometric characterizations were also given by Bisi and Bracci [Reference Bisi and Bracci2] but such characterizations are not so practical for determining whether a given LFM is a self-map of the ball.
Cowen and MacCluer’s results were improved upon by Richman [Reference Richman10] who showed how to determine t in terms of eigenvalues and eigenvectors of
![]() $m_{\phi }$
for certain cases. Richman’s approach depends on the fixed point behavior of
$m_{\phi }$
for certain cases. Richman’s approach depends on the fixed point behavior of
![]() $\phi $
. In particular, if
$\phi $
. In particular, if
![]() $\phi $
has no interior fixed point, it is known that
$\phi $
has no interior fixed point, it is known that
![]() $\phi $
has a boundary fixed point. In such a case, the positive multiple t can be determined uniquely. In the case that
$\phi $
has a boundary fixed point. In such a case, the positive multiple t can be determined uniquely. In the case that
![]() $\phi $
has an interior fixed point, the best results one can obtain is given in terms of bounds (upper and lower) on t.
$\phi $
has an interior fixed point, the best results one can obtain is given in terms of bounds (upper and lower) on t.
Our goal is determine when such a LFM is a self-map of the unit ball in the spirit of the folklore results codified by Martín without resorting to fixed point behavior. We aim to give an easily verifiable criterion dependent only on the coefficients of the LFM. This will extend Richman’s results to the general case of an interior fixed point and give an alternative criterion of determining when a given LFM is a self-map of the ball. Our approach will lie in the realization that the image of the unit ball under a LFM is a translated ellipsoid. After determining the translation, we recognize the ellipsoid as a perturbation of the unit ball. We thus apply some basic tools from linear algebra in order to obtain our desired result. We began with a basic lemma about perturbations.
Lemma 6.1 For
![]() $\alpha =(\alpha _1,\ldots , \alpha _N) \in \mathbb {B}^N\backslash \{0\}$
and
$\alpha =(\alpha _1,\ldots , \alpha _N) \in \mathbb {B}^N\backslash \{0\}$
and
![]() $s=\sqrt {1-|\alpha |^2}$
, let
$s=\sqrt {1-|\alpha |^2}$
, let
![]() $\Omega _N=s\beta -sI-\beta $
with
$\Omega _N=s\beta -sI-\beta $
with
![]() $\beta =\frac {1}{|\alpha |^2}(\alpha _i\overline {\alpha _j}),$
where I is the
$\beta =\frac {1}{|\alpha |^2}(\alpha _i\overline {\alpha _j}),$
where I is the
![]() $N \times N$
identity matrix and
$N \times N$
identity matrix and
![]() $(\alpha _i\overline {\alpha _j})$
is the
$(\alpha _i\overline {\alpha _j})$
is the
![]() $N \times N$
matrix with
$N \times N$
matrix with
![]() $ij{\text {th}}$
entry
$ij{\text {th}}$
entry
![]() $\alpha _i\overline {\alpha _j}$
. Then, we have the following:
$\alpha _i\overline {\alpha _j}$
. Then, we have the following:
Proof First, we recall the Sherman–Morrison formula [Reference Press, Flannery, Teukolsky and Vetterling9] which states that for an invertible square matrix A and column vectors
![]() $u,v$
such that
$u,v$
such that
![]() $1+\overline {v}^TA^{-1}u \neq 0$
, we have
$1+\overline {v}^TA^{-1}u \neq 0$
, we have
 $$ \begin{align*}\left(A+u\overline{v}^T\right)^{-1}=A^{-1}-\frac{A^{-1}u\overline{v}^TA^{-1}}{1+\overline{v}^TA^{-1}u},\end{align*} $$
$$ \begin{align*}\left(A+u\overline{v}^T\right)^{-1}=A^{-1}-\frac{A^{-1}u\overline{v}^TA^{-1}}{1+\overline{v}^TA^{-1}u},\end{align*} $$
where
![]() $u\overline {v}^T$
is the outer product of u and v.
$u\overline {v}^T$
is the outer product of u and v.
We realize that we may write
![]() $\Omega _N$
as the sum of an invertible matrix and outer product given by
$\Omega _N$
as the sum of an invertible matrix and outer product given by
 $$ \begin{align*}\Omega_N=-sI+(s-1)\beta=-sI+\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha \overline{\left[\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha\right]}^T,\end{align*} $$
$$ \begin{align*}\Omega_N=-sI+(s-1)\beta=-sI+\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha \overline{\left[\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha\right]}^T,\end{align*} $$
and we may thus apply the Sherman–Morrison formula. We obtain the following:
 $$ \begin{align*} \Omega_N^{-1}&=\left(-sI+\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha \overline{\left[\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha\right]}^T\right)^{-1}\\ &=-\frac{1}{s}I+\frac{-\frac{(s-1)}{s^2|\alpha|^2}(\alpha_i\overline{\alpha_j})}{1-\frac{(s-1)}{s|\alpha|^2}|\alpha|^2}=-\frac{1}{s}I-\frac{(s-1)}{s|\alpha|^2}\frac{(\alpha_i\overline{\alpha_j})}{(s-(s-1))}\\ &=\frac{-|\alpha|^2I-(s-1)(\alpha_i\overline{\alpha_j})}{s|\alpha|^2}\\ &=-\frac{1}{s|\alpha|^2}\left(|\alpha|^2+(s-1)(\alpha_i\overline{\alpha_j})\right)=-\frac{1+(s-1)\beta}{s}.\\[-40pt] \end{align*} $$
$$ \begin{align*} \Omega_N^{-1}&=\left(-sI+\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha \overline{\left[\left(\frac{\sqrt{s-1}}{|\alpha|}\right)\alpha\right]}^T\right)^{-1}\\ &=-\frac{1}{s}I+\frac{-\frac{(s-1)}{s^2|\alpha|^2}(\alpha_i\overline{\alpha_j})}{1-\frac{(s-1)}{s|\alpha|^2}|\alpha|^2}=-\frac{1}{s}I-\frac{(s-1)}{s|\alpha|^2}\frac{(\alpha_i\overline{\alpha_j})}{(s-(s-1))}\\ &=\frac{-|\alpha|^2I-(s-1)(\alpha_i\overline{\alpha_j})}{s|\alpha|^2}\\ &=-\frac{1}{s|\alpha|^2}\left(|\alpha|^2+(s-1)(\alpha_i\overline{\alpha_j})\right)=-\frac{1+(s-1)\beta}{s}.\\[-40pt] \end{align*} $$
We now have the following main result. We presume
![]() $C \neq 0$
to avoid the linear case and assume
$C \neq 0$
to avoid the linear case and assume
![]() $|D|^2>|C|^2$
.
$|D|^2>|C|^2$
.
Theorem 6.2 Let
![]() $M_i$
represent the
$M_i$
represent the
![]() $i{\textit {th}}$
row of the matrix M and
$i{\textit {th}}$
row of the matrix M and
![]() $s=\frac {\sqrt {|D|^2-|C|^2}}{|D|}$
. A LFM
$s=\frac {\sqrt {|D|^2-|C|^2}}{|D|}$
. A LFM
is a self-map of
![]() $\mathbb {B}^N$
if and only if
$\mathbb {B}^N$
if and only if
 $$ \begin{align*} &|BD-AC|^2+\left|\left(BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i\right|^2\\ &-2\biggl< BD-AC, \left(BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i \biggr> \leq (|D|^2-|C|^2)^2 \end{align*} $$
$$ \begin{align*} &|BD-AC|^2+\left|\left(BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i\right|^2\\ &-2\biggl< BD-AC, \left(BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i \biggr> \leq (|D|^2-|C|^2)^2 \end{align*} $$
for all
![]() $1 \leq i \leq N$
.
$1 \leq i \leq N$
.
Proof If
![]() $\phi $
is a self-map of
$\phi $
is a self-map of
![]() $\mathbb {B}^N$
, then we saw
$\mathbb {B}^N$
, then we saw
![]() $\mathbb {B}^N$
will map onto an ellipsoid inside of
$\mathbb {B}^N$
will map onto an ellipsoid inside of
![]() $\mathbb {B}^N$
. Hence,
$\mathbb {B}^N$
. Hence,
![]() $\phi $
can be written as
$\phi $
can be written as
where U is an
![]() $N \times N$
unitary matrix, R is a compression matrix,
$N \times N$
unitary matrix, R is a compression matrix,
![]() $\phi _{\alpha }$
is equal to equation (5.4), and
$\phi _{\alpha }$
is equal to equation (5.4), and
![]() $M=(m_1,\ldots , m_N)^T$
is the center of the ellipsoid given by
$M=(m_1,\ldots , m_N)^T$
is the center of the ellipsoid given by
![]() $\phi (\mathbb {B}^N)$
.
$\phi (\mathbb {B}^N)$
.
Next, we let
![]() $\beta =\frac {1}{|\alpha |^2}(\alpha _i \overline {\alpha _j}),$
where
$\beta =\frac {1}{|\alpha |^2}(\alpha _i \overline {\alpha _j}),$
where
![]() $\alpha _i \overline {\alpha _j}$
represents the
$\alpha _i \overline {\alpha _j}$
represents the
![]() ${ij}{\text {th}}$
entry of an
${ij}{\text {th}}$
entry of an
![]() $N \times N$
matrix, we note that
$N \times N$
matrix, we note that
![]() $\phi _{\alpha }(z)=\frac {\alpha -(s+\beta -s\beta )z}{1-\alpha ^*z}$
. A computation shows that we must have
$\phi _{\alpha }(z)=\frac {\alpha -(s+\beta -s\beta )z}{1-\alpha ^*z}$
. A computation shows that we must have
where
![]() $\Gamma '=(m_i\overline {\alpha _j})$
.
$\Gamma '=(m_i\overline {\alpha _j})$
.
It follows that we must have
![]() $C=-\alpha $
and
$C=-\alpha $
and
![]() $D=1$
. Thus
$D=1$
. Thus
![]() $|\alpha |^2=|C|^2$
. Let
$|\alpha |^2=|C|^2$
. Let
![]() $\Gamma =-\Gamma '=(m_i\overline {c_j})$
. Comparing the numerators of 6.3 implies
$\Gamma =-\Gamma '=(m_i\overline {c_j})$
. Comparing the numerators of 6.3 implies
![]() $B=M+RU\alpha $
and
$B=M+RU\alpha $
and
![]() $A=RU(s\beta -s-\beta )-\Gamma '$
. Thus, since
$A=RU(s\beta -s-\beta )-\Gamma '$
. Thus, since
![]() $C=-\alpha $
, we have
$C=-\alpha $
, we have
![]() $M=B+\left (A-\Gamma \right )(s\beta -s-\beta )^{-1}C$
which we may rearrange as
$M=B+\left (A-\Gamma \right )(s\beta -s-\beta )^{-1}C$
which we may rearrange as
 $$ \begin{align} M+\Gamma\left(-\frac{1}{s}I-\frac{s-1}{s|C|^2}(c_i\overline{c_j})\right)C=B+A\left(-\frac{1}{s}I-\frac{s-1}{s|C|^2}(c_i\overline{c_j})\right)C. \end{align} $$
$$ \begin{align} M+\Gamma\left(-\frac{1}{s}I-\frac{s-1}{s|C|^2}(c_i\overline{c_j})\right)C=B+A\left(-\frac{1}{s}I-\frac{s-1}{s|C|^2}(c_i\overline{c_j})\right)C. \end{align} $$
Noting that
![]() $(c_i\overline {c_j})C=|C|^2C$
, the left-hand side of 6.4 gives us
$(c_i\overline {c_j})C=|C|^2C$
, the left-hand side of 6.4 gives us
Likewise, after some simplification, we see that the right-hand side of 6.4 gives
![]() $B-AC$
. Thus, we have
$B-AC$
. Thus, we have
Next, since
![]() $\Gamma =MC^*=\left (\frac {B-AC}{1-|C|^2}\right )C^*$
, we have that
$\Gamma =MC^*=\left (\frac {B-AC}{1-|C|^2}\right )C^*$
, we have that
 $$ \begin{align*} RU&=\left(A-\Gamma\right)(s\beta-s-\beta)^{-1}\\ &=\left(A-\Gamma\right)\left(-\frac{1}{s|C|^2}\left[|C|^2I+(s-1)(c_i\overline{c_j})\right]\right)\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}A(c_i\overline{c_j})+\frac{(s-1)}{s|C|^2}\Gamma (c_i \overline{c_j})+\frac{1}{s}\Gamma\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}ACC^*+\Gamma.\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}ACC^*+\left(\frac{B-AC}{1-|C|^2}\right)C^*\\ &=-\frac{1}{s}A+\frac{BC^*}{1-|C|^2}-\frac{s-(1-|C|^2)}{s|C|^2(1-|C|^2)}ACC^*\\ &=\frac{BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)}{1-|C|^2}. \end{align*} $$
$$ \begin{align*} RU&=\left(A-\Gamma\right)(s\beta-s-\beta)^{-1}\\ &=\left(A-\Gamma\right)\left(-\frac{1}{s|C|^2}\left[|C|^2I+(s-1)(c_i\overline{c_j})\right]\right)\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}A(c_i\overline{c_j})+\frac{(s-1)}{s|C|^2}\Gamma (c_i \overline{c_j})+\frac{1}{s}\Gamma\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}ACC^*+\Gamma.\\ &=-\frac{1}{s}A-\frac{(s-1)}{s|C|^2}ACC^*+\left(\frac{B-AC}{1-|C|^2}\right)C^*\\ &=-\frac{1}{s}A+\frac{BC^*}{1-|C|^2}-\frac{s-(1-|C|^2)}{s|C|^2(1-|C|^2)}ACC^*\\ &=\frac{BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)}{1-|C|^2}. \end{align*} $$
Next, we let
![]() $RU_i$
represent the
$RU_i$
represent the
![]() $i{\text {th}}$
row of
$i{\text {th}}$
row of
![]() $RU$
. We apply the law of cosines to find the length of the vector connecting the displacement vector M and
$RU$
. We apply the law of cosines to find the length of the vector connecting the displacement vector M and
![]() $RU_i$
for each i. In order to remain in the unit ball, this set of i vectors must each be less than or equal to
$RU_i$
for each i. In order to remain in the unit ball, this set of i vectors must each be less than or equal to
![]() $1$
. That is, we must have
$1$
. That is, we must have
for all
![]() $1 \leq i \leq N$
.
$1 \leq i \leq N$
.
After multiplying the inequality by
![]() $1-|C|^2$
and rearranging, we obtain the set of inequalities
$1-|C|^2$
and rearranging, we obtain the set of inequalities
 $$ \begin{align*} &|B-AC|^2+\left|\left(BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i\right|^2\\ &-2\biggl< B-AC, \left(BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i \biggr>\leq (1-|C|^2)^2 \end{align*} $$
$$ \begin{align*} &|B-AC|^2+\left|\left(BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i\right|^2\\ &-2\biggl< B-AC, \left(BC^*-A\left(s+(1-s)\frac{CC^*}{|C|^2}\right)\right)_i \biggr>\leq (1-|C|^2)^2 \end{align*} $$
for all
![]() $1 \leq i \leq N$
.
$1 \leq i \leq N$
.
Finally, returning from our normalized case of
![]() $D \neq 1$
, we obtain our results.
$D \neq 1$
, we obtain our results.
The linear case follows quite simply. We have
![]() $\phi (z)=Az+b$
. Let
$\phi (z)=Az+b$
. Let
![]() $A_i$
represent the ith row of the matrix A. By the same reasoning as above, we require
$A_i$
represent the ith row of the matrix A. By the same reasoning as above, we require
for all
![]() $1 \leq i \leq N$
.
$1 \leq i \leq N$
.
Example 6.3 Let
![]() $\phi $
be the LFM in two complex variables given by
$\phi $
be the LFM in two complex variables given by
Identifying
![]() $\langle z, C \rangle $
with
$\langle z, C \rangle $
with
![]() $C^*z$
, we can write this as
$C^*z$
, we can write this as
 $$ \begin{align*}\left( \frac{z_1+1}{-z_1+3}, \frac{2z_2}{-z_1+3} \right)=\frac{\begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix}\begin{pmatrix} z_1 \\ z_2 \end{pmatrix} +\begin{pmatrix} 1 \\ 0 \end{pmatrix}}{(-1, 0)^T(z_1, z_2)+3}.\end{align*} $$
$$ \begin{align*}\left( \frac{z_1+1}{-z_1+3}, \frac{2z_2}{-z_1+3} \right)=\frac{\begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix}\begin{pmatrix} z_1 \\ z_2 \end{pmatrix} +\begin{pmatrix} 1 \\ 0 \end{pmatrix}}{(-1, 0)^T(z_1, z_2)+3}.\end{align*} $$
Thus, we have
 $A=\begin {pmatrix} 1 & 0 \\ 0 & 2 \end {pmatrix}$
,
$A=\begin {pmatrix} 1 & 0 \\ 0 & 2 \end {pmatrix}$
,
![]() $B=(1, 0)^T$
,
$B=(1, 0)^T$
,
![]() $C=(-1, 0)^T$
, and
$C=(-1, 0)^T$
, and
![]() $D=3$
. Hence,
$D=3$
. Hence,
![]() $BD-AC=(4,0)^T$
and
$BD-AC=(4,0)^T$
and
 $$ \begin{align*}BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)=\begin{pmatrix} -4 & 0 \\ 0 & 4\sqrt{2} \end{pmatrix}.\end{align*} $$
$$ \begin{align*}BC^*-A\overline{D}\left(s+(1-s)\frac{CC^*}{|C|^2}\right)=\begin{pmatrix} -4 & 0 \\ 0 & 4\sqrt{2} \end{pmatrix}.\end{align*} $$
Thus, we have
 $$ \begin{align*} &|(4, 0)|^2+|(-4,0)|^2-2\langle (4,0), (-4,0) \rangle &=64=(|D|^2-|C|^2)^2\\ &|(4, 0)|^2+|(0,4\sqrt{2})|^2-2\langle (4,0), (0,4\sqrt{2}) \rangle &=46<64=(|D|^2-|C|^2)^2. \end{align*} $$
$$ \begin{align*} &|(4, 0)|^2+|(-4,0)|^2-2\langle (4,0), (-4,0) \rangle &=64=(|D|^2-|C|^2)^2\\ &|(4, 0)|^2+|(0,4\sqrt{2})|^2-2\langle (4,0), (0,4\sqrt{2}) \rangle &=46<64=(|D|^2-|C|^2)^2. \end{align*} $$
Hence,
![]() $\phi $
is a self-map of the unit ball.
$\phi $
is a self-map of the unit ball.
One final comment regarding this result. As seen in the example, equality is achieved precisely when the self-map has no interior fixed points. Thus, the derived criteria for determining whether a LFM is a self-map of the unit ball also tells us whether our map has an interior fixed point or not. If there is no interior fixed point, then it is well known that our map must have a privileged fixed point on the boundary, known as the Denjoy–Wolff point [Reference MacCluer6].
Acknowledgment
The author would like to thank Brittney Miller and Chris Felder for fruitful conversations regarding analytic self-maps of the disk. The author would also like to thank Ralph Bremigan for recommending the use of Bruhat decomposition.