No CrossRef data available.
Article contents
Decomposition of topological Azumaya algebras
Published online by Cambridge University Press: 29 June 2021
Abstract
Let 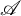 $\mathscr {A}$
be a topological Azumaya algebra of degree
$\mathscr {A}$
be a topological Azumaya algebra of degree 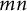 $mn$
over a CW complex X. We give conditions for the positive integers m and n, and the space X so that
$mn$
over a CW complex X. We give conditions for the positive integers m and n, and the space X so that 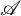 $\mathscr {A}$
can be decomposed as the tensor product of topological Azumaya algebras of degrees m and n. Then we prove that if
$\mathscr {A}$
can be decomposed as the tensor product of topological Azumaya algebras of degrees m and n. Then we prove that if 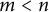 $m<n$
and the dimension of X is higher than
$m<n$
and the dimension of X is higher than 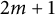 $2m+1$
,
$2m+1$
, 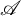 $\mathscr {A}$
may not have such decomposition.
$\mathscr {A}$
may not have such decomposition.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Antieau, B. and Williams, B., The topological period-index problem over 6-complexes. J. Topol. 7(2013), no. 3, 617–640. http://doi.org/10.1112/jtopol/jtt042
CrossRefGoogle Scholar
Antieau, B. and Williams, B., Unramified division algebras do not always contain Azumaya maximal orders. Invent. Math. 197(2014), no. 1, 47–56. http://doi.org/10.1007/s00222-013-0479-7
CrossRefGoogle Scholar
Antieau, B. and Williams, B., The period-index problem for twisted topological K-theory. Geom. Topol. 18(2014), no. 2, 1115–1148. http://doi.org/10.2140/gt.2014.18.1115
CrossRefGoogle Scholar
Auslander, M. and Goldman, O., The Brauer group of a commutative ring. Trans. Amer. Math. Soc.
97(1960), no. 3, 367–409. http://doi.org/10.1090/S0002-9947-1960-0121392-6
CrossRefGoogle Scholar
Azumaya, G., On maximally central algebras. Nagoya Math. J. 2(1951), 119–150. http://doi.org/10.1017/S0027763000010114
CrossRefGoogle Scholar
Bott, R., The space of loops on a Lie group. Michigan Math. J. 5(1958), no. 1, 35–61. http://doi.org/10.1307/mmj/1028998010
CrossRefGoogle Scholar
Grothendieck, A.,
Le groupe de Brauer: I. Algèbres d’Azumaya et interprétations diverses
. In: Séminaire Bourbaki: années 1964/65 1965/66, exposés 277-312, Séminaire Bourbaki, 9, Société mathématique de France, 1966, pp. 199–219. talk:290.Google Scholar
Mimura, M., Chapter 19—Homotopy theory of Lie groups. In: James, I. (ed.), Handbook of algebraic topology. North-Holland, Amsterdam, 1995, pp. 951–991. http://doi.org/10.1016/B978-044481779-2/50020-1
CrossRefGoogle Scholar
Saltman, D. J., Lectures on division algebras. CBMS Reg. Conf. Ser. Math., 94, AMS, Providence, RI, 1999; on behalf of CBMS, Washington, DC. http://doi.org/10.1090/cbms/094
CrossRefGoogle Scholar
Spanier, E. H., Algebraic topology. Springer, New York, NY, 1981. http://doi.org/10.1007/978-1-4684-9322-1
CrossRefGoogle Scholar
Steenrod, N., The topology of fibre bundles (PMS-14). Princeton University Press, Princeton, NJ, 1951. http://doi.org/10.1515/9781400883875
CrossRefGoogle Scholar



