Article contents
Almost Gorenstein rings arising from fiber products
Published online by Cambridge University Press: 10 July 2020
Abstract
The purpose of this paper is, as part of the stratification of Cohen–Macaulay rings, to investigate the question of when the fiber products are almost Gorenstein rings. We show that the fiber product 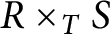 $R \times _T S$
of Cohen–Macaulay local rings R, S of the same dimension
$R \times _T S$
of Cohen–Macaulay local rings R, S of the same dimension 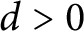 $d>0$
over a regular local ring T with
$d>0$
over a regular local ring T with 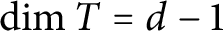 $\dim T=d-1$
is an almost Gorenstein ring if and only if so are R and S. In addition, the other generalizations of Gorenstein properties are also explored.
$\dim T=d-1$
is an almost Gorenstein ring if and only if so are R and S. In addition, the other generalizations of Gorenstein properties are also explored.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The first author was partially supported by JSPS Grant-in-Aid for Young Scientists 20K14299 and JSPS Overseas Research Fellowships. The second author was partially supported by JSPS Grant-in-Aid for Scientific Research (C) 16K05112. The third author was partially supported by Grant-in-Aid for JSPS Fellows 20J10517.
References
- 7
- Cited by



