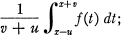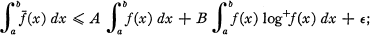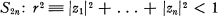Research Article
On Polynomial Extensions Of Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-2
-
- Article
-
- You have access
- Export citation
A Theorem On Zariski Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-4
-
- Article
-
- You have access
- Export citation
Certain Diophantine Equations Linear In One Unknown
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 5-12
-
- Article
-
- You have access
- Export citation
A Class Of Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-28
-
- Article
-
- You have access
- Export citation
The Normalizer Of Certain Modular Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-31
-
- Article
-
- You have access
- Export citation
On Unitary and Symmetric Matrices With Real Quaternion Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 32-39
-
- Article
-
- You have access
- Export citation
Submethods Of Regular Matrix Summability Methods
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-46
-
- Article
-
- You have access
- Export citation
Entire Solutions Of The Functional Equation f(f(z)) = g(z)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 47-48
-
- Article
-
- You have access
- Export citation
On An Inversion Formula For The Laplace Transformation, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-52
-
- Article
-
- You have access
- Export citation
A Regular Singular Functional
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 53-68
-
- Article
-
- You have access
- Export citation
A Condition For Existence Of Moments Of Infinitely Divisible Distributions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-71
-
- Article
-
- You have access
- Export citation
On Disconjugate Differential Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 72-81
-
- Article
-
- You have access
- Export citation
On a Theorem Of Le Roux
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-85
-
- Article
-
- You have access
- Export citation
Uniqueness In Boundary Value Problems For The Second Order Hyperbolic Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-96
-
- Article
-
- You have access
- Export citation
Asymptotic Solution Of Differential Equations In a Domain Containing a Regular Singular Point
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-104
-
- Article
-
- You have access
- Export citation
Differentiable Points Of Arcs In Conformal 3-Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-118
-
- Article
-
- You have access
- Export citation
Pencils Of Polarities In Projective Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-144
-
- Article
-
- You have access
- Export citation
On Connections Of Cartan
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-156
-
- Article
-
- You have access
- Export citation
A Generalization Of An Inequality Of Hardy and Littlewood
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-170
-
- Article
-
- You have access
- Export citation
Harmonic and Analytic Functions Of Several Variables and The Maximal Theorem Of Hardy and Littlewood
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 171-183
-
- Article
-
- You have access
- Export citation



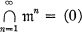
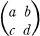
 .
.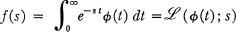
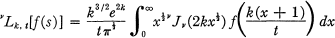
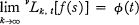
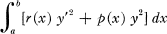
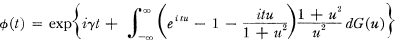
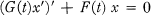
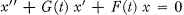
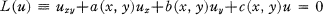
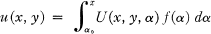
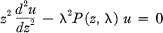
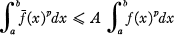
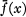 is defined as the supremum of the numbers
is defined as the supremum of the numbers