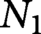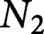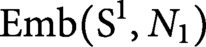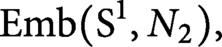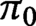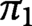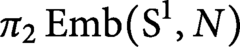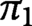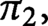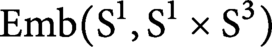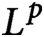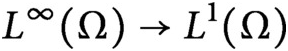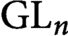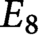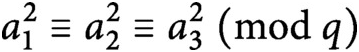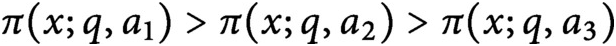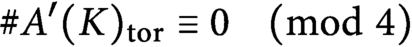Article
Spaces of knotted circles and exotic smooth structures
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2020, pp. 1-23
-
- Article
-
- You have access
- Open access
- Export citation
On a family of torsional creep problems in Finsler metrics
- Part of:
-
- Published online by Cambridge University Press:
- 02 September 2020, pp. 24-41
-
- Article
- Export citation
Möbius automorphisms of surfaces with many circles
- Part of:
-
- Published online by Cambridge University Press:
- 02 September 2020, pp. 42-71
-
- Article
- Export citation
Action convergence of operators and graphs
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2020, pp. 72-121
-
- Article
-
- You have access
- Open access
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
-
- Article
-
- You have access
- Open access
- Export citation
Some complexity results in the theory of normal numbers
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2020, pp. 170-198
-
- Article
- Export citation
Tropical geometry and Newton–Okounkov cones for Grassmannian of planes from compactifications
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2020, pp. 199-231
-
- Article
- Export citation
Densities in certain three-way prime number races
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2020, pp. 232-265
-
- Article
- Export citation
Divisibility of torsion subgroups of abelian surfaces over number fields
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2020, pp. 266-298
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CJM volume 74 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 February 2022, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
CJM volume 74 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 11 February 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation