Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-26T03:58:15.632Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisted Vertex Operators and Unitary Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Fulin Chen ,
Yun Gao ,
Naihuan Jing  and
Shaobin Tan
Fulin Chen
Affiliation:
Department of Mathematics, Xiamen University, Xiamen, China 361005. e-mail: fulinchen@amss.ac.cn, tans@xmu.edu.cn
Yun Gao
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3. e-mail: , ygao@yorku.ca
Naihuan Jing
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC, USA 27695. jing@math.ncsu.edu
Shaobin Tan
Affiliation:
Department of Mathematics, Xiamen University, Xiamen, China 361005. e-mail: fulinchen@amss.ac.cn, tans@xmu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A representation of the central extension of the unitary Lie algebra coordinated with a skew Laurent polynomial ring is constructed using vertex operators over an integral 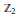${{\mathbb{Z}}_{2}}$-lattice. The irreducible decomposition of the representation is explicitly computed and described. As a by-product, some fundamental representations of affine Kac–Moody Lie algebra of type 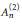$A_{n}^{\left( 2 \right)}$ are recovered by the new method.

Keywords

17B6017B69Lie algebravertex operatorrepresentation theory
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 3 , 01 June 2015 , pp. 573 - 596
Copyright
Copyright © Canadian Mathematical Society 2015

References

[ABG] Allison, B. N., Benkart, G., and Gao, Y., Lie algebras graded by the root system BCr,r≥ 2. Mem.Amer. Math. Soc. 158(2002), no. 751.Google Scholar
[AF] Allison, B. N. and Faulkner, J. R., Nonassociative coefficient algebras for Steinberg unitary Lie algebras. J. Algebra 161(1993), no. 1, 1–19. http://dx.doi.org/10.1006/jabr.1993.1202 Google Scholar
[B] Billig, Y., Principal vertex operator representations for toroidal Lie algebras. J. Math. Phys. 39(1998), no. 7, 3844–3864.http://dx.doi.org/10.1063/1.532472 Google Scholar
[BGT] Berman, S., Gao, Y., and Tan, S., A unified view on vertex operator construction. Israel J. Math. 134(2003), 29–60. http://dx.doi.org/10.1007/BF02787402 Google Scholar
[BS] Berman, S. and Szmigielski, J., Principal realization for the extended affine Lie algebra of type sl2with coordinates in a simple quantum torus with two generators. Contemp. Math., 248, American Mathematical Society, Providence, RI, 1999, 39–67.Google Scholar
[EM] Eswara Rao, S. and Moody, R. V., Vertex representations for n-toroidal Lie algebras and a generalization of the Virasoro algebra. Comm. Math. Phys. 159(1994), no. 2, 239–264.http://dx.doi.org/10.1007/BF02102638 Google Scholar
[FJ] Frenkel, I. B., Jing, N. H., Vertex representations of quantum affine Lie algebras. Proc. Nat. Acad. Sci. U.S.A. 85(1988), no. 24, 9373–9377. http://dx.doi.org/10.1073/pnas.85.24.9373 Google Scholar
[FJW] Frenkel, I. B., Jing, N., and Wang, W., Vertex representations via finite groups and the McKay correspondence. Internat. Math. Res. Notices 2000, no. 4, 195–222.Google Scholar
[FK] Frenkel, I.B. and Kac, V., Basic Representations of affine Lie algebras and dual resonance models. Invent. Math. 62(1980/81), no. 1, 23–66. http://dx.doi.org/10.1007/BF01391662 Google Scholar
[FLM] Frenkel, I. B., Lepowsky, J., and Meurman, A., Vertex operator algebras and the Monster. Pure and Applied Mathematics, 134, Academic Press, Boston, MA, 1988.Google Scholar
[G1] Gao, Y., Steinberg unitary Lie algebras and skew–dihedral homology. J. Algebra 179(1996), no. 1, 261–304.http://dx.doi.org/10.1006/jabr.1996.0013 Google Scholar
[G2] Gao, Y., Involutive Lie algebras graded by finite root systems and compact forms of IM algebras. Math. Z. 223(1996), no. 4, 651–672. http://dx.doi.org/10.1007/PL00004280 Google Scholar
[G3] Gao, Y., Vertex operators arising from the homogeneous realization for ĝlN. Comm. Math. Phys. 211(2000), no. 3, 745–777. http://dx.doi.org/10.1007/s00220005083 Google Scholar
[G4] Gao, Y., Representations of extended affine Lie algebras coordinatized by certain quantum tori. Compositio Math. 123(2000), no. 1, 1–25. http://dx.doi.org/10.1023/A:1001830622499 Google Scholar
[J] Jing, N., Twisted vertex representations of the quantum affine algebras. Invent. Math. 102(1990), no. 3, 663–690.http://dx.doi.org/10.1007/BF01233443 Google Scholar
[KKLW] Kac, V. G., Kazhdan, D. A., Lepowsky, J., and L.Wilson, R., Realization of the basic representations of the Euclidean Lie algebras. Advances in Math. 42(1981), no. 1, 83–112.http://dx.doi.org/10.1016/0001-8708(81)90053-0 Google Scholar
[KL] Kassel, C. and Loday, J.-L., Extensions centrales d’algèbres de Lie. Ann. Inst. Fourier (Grenoble) 32(1982), no. 4, 119–142.http://dx.doi.org/10.5802/aif.896 Google Scholar
[LW] Lepowsky, J. and Wilson, R. L., Construction of the affine Lie algebra A(1) 1. Commun. Math. Phys. 62(1978), no. 1, 43–53. http://dx.doi.org/10.1007/BF01940329 Google Scholar
[MRY] Moody, R. V., Eswara Rao, S., and Yokomuma, T., Toroidal lie algebras and vertex representations. Geom. Dedicata 35(1990), no. 1–3, 283–307.Google Scholar
[S] Segal, G., Unitary representations of some infinite-dimensional groups. Commun. Math. Phys. 80(1981), no. 3, 301–342.http://dx.doi.org/10.1007/BF01208274 Google Scholar
[T1] Tan, S., TKK algebras and vertex operator representations. J. Algebra 211(1999), no. 1, 298–342.http://dx.doi.org/10.1006/jabr.1998.7604 Google Scholar
[T2] Tan, S., Principal construction of the toroidal Lie algebra of type A1. Math. Z. 230(1999), no. 4, 621–657.http://dx.doi.org/10.1007/PL00004710 Google Scholar
[T3] Tan, S., Vertex operator representations for toroidal Lie algebras of type Bl. Comm. Algebra 27(1999),no. 8, 3593–3618. http://dx.doi.org/10.1080/00927879908826650 Google Scholar
[W] Wakimoto, M., Twisted vertex operators and A–D–E representations. arxiv:math/0111018v2Google Scholar
[Y] Yamada, H. K., Extended affine Lie algebras and their vertex representations. Publ. Res. Inst. Math. Sci. 25(1989), no. 4, 587–603. http://dx.doi.org/10.2977/prims/1195173183 Google Scholar