Article contents
Toric Degenerations, Tropical Curve, and Gromov–Witten Invariants of Fano Manifolds
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper, we give a tropical method for computing Gromov–Witten type invariants of Fano manifolds of special type. This method applies to those Fano manifolds that admit toric degenerations to toric Fano varieties with singularities allowing small resolutions. Examples include (generalized) flag manifolds of type 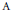 $\text{A}$ and some moduli space of rank two bundles on a genus two curve.
$\text{A}$ and some moduli space of rank two bundles on a genus two curve.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 1
- Cited by


