Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-18T10:11:37.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification Groups of Abelian Local Field Extensions

Published online by Cambridge University Press:  20 November 2018

Murray A. Marshall
Murray A. Marshall*
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a local field; that is, a complete discrete-valued field having a perfect residue class field. If L is a finite Galois extension of k then L is also a local field. Let G denote the Galois group GL|k. Then the nth ramification group Gn is defined by

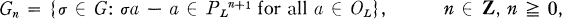
where OL, denotes the ring of integers of L, and PL is the prime ideal of OL. The ramification groups form a descending chain of invariant subgroups of G:

1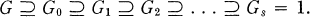

In this paper, an attempt is made to characterize (in terms of the arithmetic of k) the ramification filters (1) obtained from abelian extensions L\k.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 2 , April 1971 , pp. 271 - 281
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Arf, C., Untersuchungen Über reinverzweigte Erweiterungen diskret bewerteter perfekter Kôrper, J. Reine Angew. Math. 181 (1939), 1–44.Google Scholar
2. Artin, E. and Tate, J., Class field theory (Benjamin, New York-Amsterdam, 1968).Google Scholar
3. Hasse, H., Normenresttheorie galoisscher Zahlkörper mit Anwendungen auf Fiihrer und Discriminante abelscher Zahlkôrper, J. Fac. Sci. Tokyo 2 (1934), 477–498.Google Scholar
4. Herbrand, J., Sur la théorie des groupes de décomposition, d'inertie, et de ramification, J. Math. Pures Appl. Sér. 9 10 (1931), 481–498.Google Scholar
5. Lang, S., Rapport sur la cohomologie des groupes (Benjamin, New York-Amsterdam, 1967).Google Scholar
6. Marshall, M., The ramification filters of abelian extensions of a local field, Ph.D. Thesis, Queen's University, Kingston, Ontario, 1969.Google Scholar
7. Marshall, M., The maximal p-extension of a local field (Can. J. Math., to appear).Google Scholar
8. Maus, E., Die gruppentheoretische Struktur der Verzweigungsgruppenreihen, J. Reine Angew. Math. 280 (1968), 1–28.Google Scholar
9. Ore, O., Additive polynomials, Trans. Amer. Math. Soc. 35 (1933), 559–584.Google Scholar
10. Pontryagin, L. S., Topological groups, translated from the second Russian edition by Brown, Aden (Gordon and Breach, New York-London-Paris, 1966).Google Scholar
11. Serre, J.-P., Groupes proalgébriques, Inst. Hautes Études Sci. Publ. Math. No. 7 (1960), 67 pp.Google Scholar
12. Serre, J.-P., Sur les corps locaux à corps résiduel algébriquement clos, Bull. Soc. Math. France 89 (1961), 105–154.Google Scholar
13. Serre, J.-P., Corps locaux, Publications de l'Institut de Mathématique de l'Université de Nancago, VIII, Actualités Sci. Indust., No. 1296 (Hermann, Paris, 1962).Google Scholar
14. Serre, J.-P., Cohomologie galoisienne, Cours au Collège de France, 1962-1963. Seconde édition, with a contribution by Jean-Louis Verdier, Lecture Notes in Mathematics 5 (Springer- Verlag, Berlin-Heidelberg-New York, 1964).Google Scholar