Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-12T09:14:27.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Products of Decomposable Positive Operators

Published online by Cambridge University Press:  20 November 2018

Terrance Quinn
Terrance Quinn*
Affiliation:
Department of Mathematics, Statistics and Computer Science, Dalhousie University, Halifax, Nova Scotia B3H3J5
*
Mailing address: Department of Mathematics University College Cork City Ireland e-mail: tquinn @bureau.ucc.ie
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent years there has been a growing interest in problems of factorization for bounded linear operators. We first show that many of these problems properly belong to the category of C*-algebras. With this interpretation, it becomes evident that the problem is fundamental both to the structure of operator algebras and the elements therein. In this paper we consider the direct integral algebra 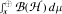with 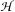separable and infinite dimensional. We generalize a theorem of Wu (1988) and characterize those decomposable operators which are products of non-negative decomposable operators. We do this by first showing that various results on operator ranges may be generalized to “measurable fields of operator ranges”.

Keywords

47A6847C15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 4 , 01 August 1994 , pp. 854 - 871
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Azoff, E. A. and Clancey, K. F., Spectral multiplicity for direct integrals of normal operators, J. Operator Theory 3(1980), 213–235.Google Scholar
2. Ballantine, C. S., Products of positive definite matrices IV, Linear Algebra Appl. 3(1970), 79–114.Google Scholar
3. Conway, J. B., A course in functional analysis, Springer-Verlag, New York, 1985.Google Scholar
4. Feldman, J. and Kadison, R. V., The closure of the regular operators in a ring of operators, Proc. Amer. Math. Soc. 5(1954), 909–916.Google Scholar
5. Fillmore, P., On products of symmetries, Canad. J. Math. 18(1966), 897–900.Google Scholar
6. Fillmore, P. and Williams, J., On operator ranges, Adv. in Math. 7(1971), 254–281.Google Scholar
7. Halmos, P., A Hilbert-space problem book, Second Ed., Springer-Verlag, New York, 1982.Google Scholar
8. Halmos, P., Bad products of good matrices, Linear and Multilinear Algebra 29(1991), 1–20.Google Scholar
9. Halmos, P. and Kakutani, S., Products of symmetries, Bull. Amer. Math. Soc. 64(1958), 77–78.Google Scholar
10. Herrero, D. A., Approximation of Hilbert-space operators I, Pitman Res. Notes in Math. 72, London 1982.Google Scholar
11. Himmellerg, C. J., Measurable relations, Fund. Math. LXXXVII(1975), 53–72.Google Scholar
12. Kadison, R. V. and Ringrose, J. G., Fundamentals in the theory of operator algebras I, II, Academic Press, New York, 1983, 1986.Google Scholar
13. Khalkhali, M., Laurie, C., Mathes, B. and Radjavi, H., Approximation by products of positive operators, J. Operator Theory, to appear.Google Scholar
14. Nussbaum, A. E., Reduction theory for unbounded closed operators in Hilbert-space, Duke Math. J. 31 (1964), 33–44.Google Scholar
15. Quinn, T., Factorization in C* -algebras: products of positive operators, Ph.D. thesis, Dalhousie Univ., Halifax, 1992.Google Scholar
16. Radjavi, H., Products of Hermitian matrices and symmetries, Proc. Amer. Math. Soc. 26(1970), 701.Google Scholar
17. Radjavi, H., On self-adjoint factorization ofoperators, Canad. J. Math. 21(1969), 1421–1426.Google Scholar
18. Stone, M. H., On unbounded operators in Hilbert space, J. Indian Math. Soc. 15(1951), 155–192.Google Scholar
19. Takesaki, M., Theory of operator algebras I, Springer-Verlag, New York, 1979.Google Scholar
20. von Neumann, J., Functional Operators II, Ann. of Math. Stud. 22, Princeton Univ. Press, Princeton, 1950.Google Scholar
21. Wu, P. Y., Products of normal operators, Canad. J. Math.(6) XL(1988), 1322–1330.Google Scholar
22. Wu, P. Y., The operator factorization problems, Linear Algebra Appl. 117(1989), 35–63.Google Scholar