Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Larson, Paul
and
Tall, Franklin D.
2014.
On the Hereditary Paracompactness of Locally Compact, Hereditarily Normal Spaces.
Canadian Mathematical Bulletin,
Vol. 57,
Issue. 3,
p.
579.
Tall, Franklin D.
2014.
PFA(S)[S]and locally compact normal spaces.
Topology and its Applications,
Vol. 162,
Issue. ,
p.
100.
Yorioka, Teruyuki
2015.
A note on a forcing related to the S‐space problem in the extension with a coherent Suslin tree.
Mathematical Logic Quarterly,
Vol. 61,
Issue. 3,
p.
169.
Fischer, A.J.
Tall, F.D.
and
Todorcevic, S.
2015.
Forcing with a coherent Souslin tree and locally countable subspaces of countably tight compact spaces.
Topology and its Applications,
Vol. 195,
Issue. ,
p.
284.
Junnila, Heikki
and
Nyikos, Peter
2016.
Compactifications and remainders of monotonically normal spaces.
Topology and its Applications,
Vol. 213,
Issue. ,
p.
80.
Tall, Franklin D.
2017.
PFA(S)[S] for the masses.
Topology and its Applications,
Vol. 232,
Issue. ,
p.
13.
Yorioka, Teruyuki
2017.
Club-Isomorphisms of Aronszajn Trees in the Extension with a Suslin Tree.
Notre Dame Journal of Formal Logic,
Vol. 58,
Issue. 3,
Dow, Alan
and
Tall, Franklin D.
2018.
Normality Versus Paracompactness in Locally Compact Spaces.
Canadian Journal of Mathematics,
Vol. 70,
Issue. 1,
p.
74.
 $L$-spaces or compact
$L$-spaces or compact  $S$-spaces. The model is one of the form
$S$-spaces. The model is one of the form 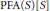 $\text{PFA}\left( S \right)\left[ S \right]$, where
$\text{PFA}\left( S \right)\left[ S \right]$, where  $S$ is a coherent Souslin tree.
$S$ is a coherent Souslin tree.

