Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T10:11:35.983Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Embedding into a Ring of an Archimedean ι-Group

Published online by Cambridge University Press:  20 November 2018

Anthony W. Hager  and
Lewis C. Robertson
Anthony W. Hager
Affiliation:
Wesley an University, Middletown, Connecticut
Lewis C. Robertson
Affiliation:
Wesley an University, Middletown, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall prove the following about the “ringification” ρA of [2] and [5] of an archimedean l-group A: (a) Any “minimal ring” containing A is ρA; (b) A ↦ ρA is a reflector; (c) ρA need not be laterally complete when A is. These constitute the solutions to the problems posed in [2] by Paul Conrad.

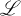1. The embedding into a ring. Let be the category which has objects archimedean l-groups A with distinguished positive weak unit eA, and morphisms l-group homomorphisms h: A → B with h(eA) = eB. Let 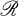be the category with objects archimedean f-rings R with identity 1R which is a weak unit, and morphisms l-ring homomorphisms h: R → S with h(lR) = 1S.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 1 - 8
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Bernau, S., Unique representations of lattice groups and normal Archimedean lattice rings, Proc. London Math. Soc. 15 (1965), 599–631.Google Scholar
2. Conrad, P., The additive group of an f-ring, Can. J. Math. 26 (1974), 1157–1168.Google Scholar
3. Gillman, L. and Jerison, M., Rings of continuous functions (Princeton, 1960).Google Scholar
4. Gleason, A., Projective topological spaces, 111. J. Math. 2 (1958), 482–489.Google Scholar
5. Hager, A. W. and Robertson, L. C., Representing and ringifying a Riesz space, Proceedings, 1975 Rome Symposium on ordered groups and rings: Symposia Mathematica 21 Bolgona (1977), 411–431.Google Scholar
6. Herrlich, H. and Strecker, G., Category theory (Boston, 1973).Google Scholar
7. Maeda, F. and Ogasawara, T., Representations of vector lattices, J. Sci. Hiroshima Univ. (A). 12 (1942), 17–35.Google Scholar
8. Veksler, A. I. and Geiler, V. A., Order and disjoint completeness of linear partially ordered spaces, Siberian Math. J. (Plenum translation. 13 (1972), 30–35.Google Scholar
9. Yosida, K., On the representation of the vector lattice, Proc. Imp. Acad. Toky. 18 (1942), 339–342.Google Scholar