Hostname: page-component-84b7d79bbc-5lx2p Total loading time: 0 Render date: 2024-07-31T20:45:24.943Z Has data issue: false hasContentIssue false
  • English
  • Français

A Localization of R[x]

Published online by Cambridge University Press:  20 November 2018

James A. Huckaba  and
Ira J. Papick
James A. Huckaba
Affiliation:
University of Missouri, Columbia, Missouri
Ira J. Papick
Affiliation:
University of Missouri, Columbia, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper, R will be a commutative integral domain with identity and x an indeterminate. If ƒ ∈ R[x], let CR(ƒ) denote the ideal of R generated by the coefficients of ƒ. Define SR = {ƒ ∈ R[x]: cR(ƒ) = R} and UR = {ƒ ∈ R(x): cR(ƒ)– 1 = R}. For a,b ∈ R, write 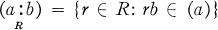. When no confusion may result, we will write c(ƒ), S, U, and (a:b). It follows that both S and U are multiplicatively closed sets in R[x] [7, Proposition 33.1], [17, Theorem F], and that R[x]s ⊆ R[x]U.

The ring R[x]s, denoted by R(x), has been the object of study of several authors (see for example [1], [2], [3], [12]). An especially interesting paper concerning R(x) is that of Arnold's [3], where he, among other things, characterizes when R(x) is a Priifer domain. We shall make special use of his results in our work.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 103 - 115
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Anderson, D. D., Multiplication ideals, multiplication rings, and the ringR(x), Can. J. Math. 28 (1976), 760–768.Google Scholar
2. Anderson, D. D., Some remarks on the ring R(x), Comment. Math., Univ. St. Pauli. 26 (1977), 137–140.Google Scholar
3. Arnold, J. T., On the ideal theory of the Kronecker function ring and the domain D(x), Can. J. Math. 21 (1969), 558–563.Google Scholar
4. Arnold, J. T. and Sheldon, P. B., Integral domains that satisfy Gauss's Lemma, Mich. Math. J. 22 (1975), 39–51.Google Scholar
5. Bourbaki, N., Commutative algebra (Addison-Wesley, Reading, Mass., 1972).Google Scholar
6. Chase, S. U., Direct products of modules, Trans. Amer. Math. Soc. 97 (1960), 457–519.Google Scholar
7. Gilmer, R., Multiplicative ideal theory (Marcel Dekker, New York, 1972).Google Scholar
8. Gilmer, R. and Huckaba, J. A., The transform formula for ideals, J. of Alg. 21 (1972), 191–215.Google Scholar
9. Gilmer, R., The pseudo-radical of a commutative ring, Pac. J. Math. 19 (1966), 275–284.Google Scholar
10. Glaz, S. and Vasconcelos, W. V., Flat ideals II, Manuscripta Math. 22 (1977), 325–341.Google Scholar
11. Harris, M. E., Some results on coherent rings, Proc. Amer. Math. Soc. 17 (1966), 474–479.Google Scholar
12. Hinkle, G. W. and Huckaba, J. A., The generalized Kronecker function ring and the ring R(x), J. Reine Angew. Math. 292 (1977), 25–36.Google Scholar
13. Kaplansky, I., Commutative rings (Allyn and Bacon, Boston, Mass., 1970).Google Scholar
14. McAdam, S., Going down in polynomial rings, Can. J. Math. 23 (1971), 704–711.Google Scholar
15. Nagata, M., Local rings (Interscience Publishers, New York, 1962).Google Scholar
16. Zariski, O. and Samuel, P., Commutative algebra, Vol. II (Van Nostrand, Princeton, 1958).Google Scholar
17. Tang, H. T., Gauss’ Lemma, Proc. Amer. Math. Soc. 35 (1972), 372–376.Google Scholar
18. Vasconcelos, W. V., Divisor theory in module categories (North-Holland, New York, 1974).Google Scholar