Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-17T17:13:17.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Jordan Loops and Decompositions of Operators

Published online by Cambridge University Press:  20 November 2018

Arlen Brown  and
Carl Pearcy
Arlen Brown
Affiliation:
Indiana University, Bloomington, Indiana
Carl Pearcy
Affiliation:
University of Michigan Ann Arbor, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 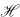be a separable, infinite dimensional, complex Hilbert space, and let 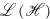denote the algebra of all bounded linear operators on 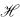. In what follows we shall denote the spectrum, essential spectrum, and left essential spectrum of an operator T in 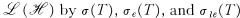, respectively. Furthermore, if 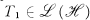and T1 is unitarily equivalent to a compact perturbation of an operator T2, then we write T1~ T2, and if the compact perturbation can be chosen to have norm less than e, we write T1 ~ T2(ϵ).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 5 , 01 October 1977 , pp. 1112 - 1119
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Apostol, C., Foias, C., and Voiculescu, D., Some results on non-quasitriangular operators. IV, Revue Roum. Math. Pures et Appl. 18 (1973), 487–514.Google Scholar
2. Brown, A. and Pearcy, C., Introduction to operator theory. Volume I: Elements of functional analysis (Springer-Verlag, to appear).Google Scholar
3. Douglas, R. G. and Pearcy, C., Invariant subspaces of non-quasitriangular operators, Proc. Conf. Op. Theory, Springer-Verlag Lecture Notes in Mathematics, Vol. 3-5 (1973), 13–57.Google Scholar
4. Foias, C., Pearcy, C., and Voiculescu, D., The staircase representation of biquasitriangular operators, Mich. Math. J. 22 (1975), 343–352.Google Scholar
5. Foias, C. Biquasitriangular operators and quasisimilarity, submitted to Indiana U. Math. J.Google Scholar
6. Halmos, P. R., Limits of shifts, Acta Sci. Math. (Szeged) 34 (1973), 131–139.Google Scholar
7. Herrero, D. and Salinas, N., Operators with disconnected spectra are dense, Bull. Amer. Math. Soc. 78(1972), 525–526.Google Scholar
8. Pearcy, C., Some recent progress in operator theory, CBMS Regional Conference Series in Mathematics, A.M.S., to appear.Google Scholar
9. Rudin, W., Real and complex analysis (McGraw-Hill, New York, 1966).Google Scholar