Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T17:08:55.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth of Selmer Groups of CM Abelian Varieties

Published online by Cambridge University Press:  20 November 2018

Meng Fai Lim  and
V. Kumar Murty
Meng Fai Lim
Affiliation:
School of Mathematics and Statistics, Central China Normal University, NO.152, Luoyu RoadWuhan Hubeih430079, China e-mail: limmf@mail.ccnu.edu.cn
V. Kumar Murty
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George St., Toronto ON, M5S 2E4Canada e-mail: murty@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 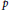$p$ be an odd prime. We study the variation of the 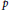$p$-rank of the Selmer groups of Abelian varieties with complex multiplication in certain towers of number fields.

Keywords

11G1511G1011R2311R34Selmer groupAbelian variety with complex multiplicationℤp–extensionp–Hilbert class tower
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 3 , 01 June 2015 , pp. 654 - 666
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Boston, N., Some cases of the Fontaine-Mazur conjecture. J. Number Theory 42(1992), no. 3, 285–291.http://dx.doi.Org/10.101 6/0022-314X(92)90093-5 Google Scholar
[2] Fontaine, J.-M. and Mazur, B., Geometric Galois representations. In: Elliptic curves, modular forms and Fermafs last theorem (Hong Kong 1993), Ser. Number Theory, I, Int. Press, Cambridge, MA, 1995, pp. 41–78.Google Scholar
[3] Golod, E. S. and šafarevič, I. R., On the class field tower. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 28(1964), 261–272.Google Scholar
[4] Greenberg, R., Galois theory for the Selmer group of an Abelian variety. Compositio Math. 136(2003), no. 3, 255–297.http://dx.doi.Org/10.1023/A:1023251032273 Google Scholar
[5] Hajir, F., On the growth of p– class groups in p–class towers. J. Algebra 188(1997), no. 1, 256–271.http://dx.doi.Org/10.1006/jabr.1996.6849 Google Scholar
[6] Iwasawa, K., On the μinvariants of ℤ1extensions. In: Number theory, algebraic geometry and commutative algebra, in honour of Yasuo Akizuki, Kinokuniya, Tokyo, 1973, pp. 1–11.Google Scholar
[7] Lubotzky, A. and Mann, A., Powerful p–groups. II. p–adic analytic groups. J. Algebra 105(1987), no. 2, 506–515. http://dx.doi.org/10.1016/0021-8693(87)90212-2 Google Scholar
[8] Matar, A., Selmer groups and generalized class field towers. Int. J. Number Theory 8(2012), no. 4, 881–909.http://dx.doi.org/10.1142/S1793042112500522 Google Scholar
[9] Mazur, B., Rational points of Abelian varieties with values in towers of number fields. Invent. Math. 18(1972), 183–266.http://dx.doi.Org/10.1007/BF01389815 Google Scholar
[10] Mazur, B. and Rubin, K., Finding large Selmer rank via an arithmetic theory of local constants. Ann. of Math. 166(2007), no. 2, 579–612. http://dx.doi.org/10.4007/annals.2007.166.579 Google Scholar
[11] Mazur, B. and Rubin, K., Growth of Selmer rank in nonabelian extensions of number fields. DukMath. J. 143(2008), no. 3, 437–461. http://dx.doi.org/10.1215/00127094-2008-025 Google Scholar
[12] Monsky, P., p–ranks of class groups in Zd p;–extensions. Math. Ann. 263(1983), no. 4, 509–514.http://dx.doi.Org/10.1007/BF01457057 Google Scholar
[13] Mumford, D., Abelian varieties. Second ed., Tata Institute of Fundamental Research Studies in Mathematics, 5, Oxford University Press, London, 1974.Google Scholar
[14] Murty, V. K. and Ouyang, Y., The growth of Selmer ranks of an Abelian variety with complex multiplication. Pure Appl. Math. Q. 2(2006), no. 2, 539–555.http://dx.doi.Org/10.4310/PAMQ.2OO6.V2.n2.a7 Google Scholar
[15] Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields. Second ed., Grundlehren der Mathematischen Wissenschaften, 323, Springer–Verlag, Berlin, 2008.Google Scholar
[16] –P. Serre, J. and Tate, J., Good reduction of abelian varieties. Ann. of Math. 88(1968), 492–517.http://dx.doi.org/10.2307/1970722 Google Scholar