Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T15:22:12.244Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact Inequalities for the Norms of Factors of Polynomials

Published online by Cambridge University Press:  20 November 2018

Peter B. Borwein
Peter B. Borwein*
Affiliation:
Department of Mathematics, Statistics and Computing Science Dalhousie University, Halifax, Nova Scotia B3H3J5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper addresses a number of questions concerning the size of factors of polynomials. Let p be a monic algebraic polynomial of degree n and suppose q1q2 … qi is a monic factor of p of degree m. Then we can, in many cases, exactly determine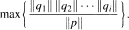

Here ‖ . ‖ is the supremum norm either on [—1, 1] or on {|z| ≤ 1}. We do this by showing that, in the interval case, for each m and n, the n-th Chebyshev polynomial is extremal. This extends work of Gel'fond, Mahler, Granville, Boyd and others. A number of variants of this problem are also considered.

Keywords

26D0530C1041A10polynomialsfactorsChebyshev polynomialsinequalities
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 4 , 01 August 1994 , pp. 687 - 698
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, Dover, New York, 1965.Google Scholar
2. Aumann, G., Satz, , überdas Verhalten von Polynomen aufKontinuen, Sitz. Preuss. Akad. Wiss. Phys.-Math. Kl., (1933), 926-931.Google Scholar
3. Beauzamy, B. and Enflo, P., Estimations de produits de polynômes, J. Number Theory 21(1985), 390-412.Google Scholar
4. Beauzamy, B., Bombieri, E., Enflo, P. and Montgomery, H. L., Products of polynomials in many variables, J. Number Theory 36(1990), 219-245.Google Scholar
5. Boyd, D. W., Two sharp inequalities for the norm of a factor of a polynomial, Mathematika, to appear.Google Scholar
6. Boyd, D. W., Sharp inequalities for the product of polynomials, to appear.Google Scholar
7. Gel'fond, A. O., Transcendental and Algebraic Numbers, Dover, New York, 1960; translation by L. F. Boron, Russion edition, 1952.Google Scholar
8. Glesser, P., Nouvelle majoration de la norme des facteurs d'un polynôme, C. R. Math. Rep. Acad. Sci. Canada 12(1990), 224-228.Google Scholar
9. Granville, A., Bounding the coefficients of a divisor of a given polynomial, Monatsh. Math. 109(1990), 271-277.Google Scholar
10. Kneser, H., Das Maximum des Produkts zweie s Polynome, Sitz. Preuss. Akad. Wiss. Phys.-Math. Kl., (1934), 429-431.Google Scholar
11. Mahler, K., An application of Jensen's formula to polynomials, Mathematika 7( 1960), 98-100.Google Scholar
12 Mahler, K., On some inequalities for polynomials in several variables, J. London Math. Soc. 37(1962), 341-344.Google Scholar
13 Mahler, K., A remark on a paper of mine on polynomials, Illinois J. Math. 8(1964), 1-4.Google Scholar
14. Mignotte, M., Some useful bounds. In: Computer Algebra, Symbolic and Algebraic Computation, (eds. B. Burchberger, et ai), Springer, New York, 1982, 259-263.Google Scholar
15. Rivlin, T., Chebyshev Polynomials, 2nd Edition, Wiley, New York, 1990.Google Scholar