Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-25T07:39:47.350Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant Formality for Actions of Torus Groups

Published online by Cambridge University Press:  20 November 2018

Laura Scull
Laura Scull*
Affiliation:
The University of British Columbia, Department of Mathematics, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2 e-mail: scull@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper contains a comparison of several definitions of equivariant formality for actions of torus groups. We develop and prove some relations between the definitions. Focusing on the case of the circle group, we use 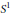${{S}^{1}}$ -equivariant minimal models to give a number of examples of 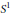${{S}^{1}}$-spaces illustrating the properties of the various definitions.

Keywords

55P9155P6255R3555S45Equivariant homotopycircle actionminimal modelrationalizationformality
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 6 , 01 December 2004 , pp. 1290 - 1307
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Borel, A., Seminar on Transformation Groups. Annals of Mathematics Studies, 46, Princeton University Press, Princeton, NJ, 1960.Google Scholar
[2] Bousfield, A.K. and Gugenheim, V. K. A.M., On PL de Rham theory and rational homotopy type. Mem. Amer.Math. Soc. 8(1976).Google Scholar
[3] Bredon, G., Equivariant Cohomology Theories. Lecture Notes in Mathematics, 34, Springer-Verlag, Berlin, 1967.Google Scholar
[4] Deligne, P., Griffiths, P., Morgan, J. and Sullivan, D., Real homotopy theory of Kähler manifolds. Invent.Math. 29(1975), 245–274 .Google Scholar
[5] Elmendorf, A., Systems of fixed point sets. Trans. Amer.Math. Soc. 277(1983), 275–284. .Google Scholar
[6] Felix, Y., Halperin, S., and Thomas, J.-C., Rational Homotopy Theory. Graduate Texts in Mathematics, 205, Springer-Verlag, New York, 2001.Google Scholar
[7] Fine, B.L. and Triantafillou, G., On the equivariant formality of Kähler manifolds with finite group action. Canad. J. Math. 45(1993), 1200–1210.Google Scholar
[8] Goresky, M., Kottwitz, R. and MacPherson, R., Equivariant cohomology, Koszul duality, and the localization theorem. Invent.Math. 131(1998), 25–83.Google Scholar
[9] Lillywhite, S., Formality in an equivariant setting. Trans. Amer. Math. Soc. 355(2003), 2771–2793.Google Scholar
[10] Mandell, M. and Scull, L., Algebraic models for equivariant homotopy theory over Abelian compact Lie groups. Math. Z. 240(2002), 261–287.Google Scholar
[11] Scull, L., Rational S1-equivariant homotopy theory. Trans. Amer. Math. Soc. 354(2001), 1–45.Google Scholar
[12] Scull, L., Formality and S1-equivariant algebraic models. Proceedings of the Northwestern University Algebraic Topology Conference, P. Goerss,Mahowald, M., and Priddy, S., eds., to appear.Google Scholar
[13] Sullivan, D., Infinitesimal computations in topology. Inst. Hautes Eudes Sci. Publ. Math. 47(1977), 269–332.Google Scholar