No CrossRef data available.
Article contents
Cubic Base Change for 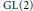 $\text{GL(2)}$
$\text{GL(2)}$
Published online by Cambridge University Press: 20 November 2018
Abstract
We prove a relative trace formula that establishes the cubic base change for 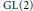 $\text{GL(2)}$. One also gets a classification of the image of base change. The case when the field extension is nonnormal gives an example where a trace formula is used to prove lifting which is not endoscopic.
$\text{GL(2)}$. One also gets a classification of the image of base change. The case when the field extension is nonnormal gives an example where a trace formula is used to prove lifting which is not endoscopic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000


