Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-7f7b94f6bd-w6m4b Total loading time: 0.184 Render date: 2022-07-01T03:11:55.429Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true } hasContentIssue true
  • English
Canadian Journal of Mathematics Canadian Journal of Mathematics

Article contents

Commutators in Factors of Type III

Published online by Cambridge University Press:  20 November 2018

Arlen Brown  and
Carl Pearcy
Arlen Brown
Affiliation:
The University of Michigan, Ann Arbor, Michigan
Carl Pearcy
Affiliation:
The University of Michigan, Ann Arbor, Michigan
Rights & Permissions[Opens in a new window]

Extract

HTML view is not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 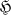denote a separable, complex Hilbert space, and let R be a von Neumann algebra acting on 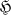. (A von Neumann algebra is a weakly closed, self-adjoint algebra of operators that contains the identity operator on its underlying space.) An element A of R is a commutator in R if there exist operators B and C in R such that A = BC — CB. The problem of specifying exactly which operators are commutators in R has been solved in certain special cases; e.g. if R is an algebra of type In (n < ∞) (2), and if R is a factor of type I∞ (1). It is the purpose of this note to treat the same problem in case R is a factor of type III. Our main result is the following theorem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 1152 - 1160
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Brown, A. and Pearcy, C., Structure of commutators of operators, Ann. Math., 82 (1965), 112—127.CrossRefGoogle Scholar
2. Deckard, D. and Pearcy, C., On continuous matrix-valued functions on a Stonian space, Pacific J. Math., 14(1964), 857–869.CrossRefGoogle Scholar
3. Lumer, G. and Rosenbloom, M., Linear operator equations, Proc. Amer. Math. Soc., 10 (1959), 32–41.CrossRefGoogle Scholar
4. Pearcy, C., On commutators of operators on Hilbert space, Proc. Amer. Math. Soc, 16 (1965), 53–59.CrossRefGoogle Scholar
You have Access
10
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Commutators in Factors of Type III
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Commutators in Factors of Type III
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Commutators in Factors of Type III
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *