Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T10:53:58.713Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded Derived Categories of Infinite Quivers: Grothendieck Duality, Reflection Functor

Published online by Cambridge University Press:  20 November 2018

Javad Asadollahi ,
Rasool Hafezi  and
Razieh Vahed
Javad Asadollahi
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran and School of Mathematics, Institute for Research in Fundamental Science (IPM), Tehran, Iran. e-mail: asadollahi@ipm.ir. vahed@ipm.ir. hafezi@ipm.ir
Rasool Hafezi
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran and School of Mathematics, Institute for Research in Fundamental Science (IPM), Tehran, Iran. e-mail: asadollahi@ipm.ir. vahed@ipm.ir. hafezi@ipm.ir
Razieh Vahed
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran and School of Mathematics, Institute for Research in Fundamental Science (IPM), Tehran, Iran. e-mail: asadollahi@ipm.ir. vahed@ipm.ir. hafezi@ipm.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study bounded derived categories of the category of representations of infinite quivers over a ring 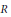$R$. In case 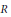$R$ is a commutative noetherian ring with a dualising complex, we investigate an equivalence similar to Grothendieck duality for these categories, while a notion of dualising complex does not apply to them. The quivers we consider are left (resp. right) rooted quivers that are either noetherian or their opposite are noetherian. We also consider reflection functor and generalize a result of Happel to noetherian rings of finite global dimension, instead of fields.

Keywords

18E3016G2018E4016D9018A40Derived CategoryGrothendieck dualityrepresentation of quiversreflection functor
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 28 - 54
Copyright
Copyright © Canadian Mathematical Society 2015

References

[AEHS] Asadollahi, J., Eshraghi, H., Hafezi, R., and Salarian, Sh., On the homotopy categories of projective and injective representations of quivers. J. Algebra 346(2011), 101–115.http://dx.doi.org/10.1016/j.jalgebra.2011.08.028 Google Scholar
[AHS] Asadollahi, J., Hafezi, R., and Salarian, Sh., Homotopy category of projective complexes and complexes of Gorenstein projective modules. J. Algebra 399(2014), 423–444. http://dx.doi.org/10.1016/j.jalgebra.2013.09.045 Google Scholar
[APR] Auslander, M., Platzeck, M. I., and Reiten, I., Coxeter functors without diagrams. Trans. Amer. Math. Soc. 250(1979), 1–46.http://dx.doi.org/10.1090/S0002-9947-1979-0530043-2 Google Scholar
[BLP] Bautista, R., Liu, S., and Paquette, C., Representation theory of strongly locally finite quivers. Proc. London Math. Soc., (3) 106(2013), no. 1, 97–162. http://dx.doi.org/10.1112/plms/pds039 Google Scholar
[BGP] Bernšteĭn, I. N., Gel’fand, I. M., and Ponomarev, V. A., Coxeter functors, and Gabriel's theorem. (Russian) Uspehi Mat. Nauk 28(1973), no. 2, 19–33.Google Scholar
[BB] Brenner, S. and Butler, M.C. R., Generalizations of the Bernstein-Gel’fand-Ponomarev reflection functors. In: Representation theory, II (Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979), Lecture Notes in Math., 832, Springer, Berlin-New York, 1980, pp. 103–169.Google Scholar
[C] Chen, X.-W., Homotopy equivalences induced by balanced pairs. J. Algebra 324(2010), no. 10, 2718–2731.http://dx.doi.org/10.1016/j.jalgebra.2010.09.002 Google Scholar
[EE1] Enochs, E. and Estrada, S., Projective representations of quivers. Comm. Algebra 33(2005), no. 10, 3467–3478. http://dx.doi.org/10.1081/AGB-200058181 Google Scholar
[EEG] Enochs, E., Estrada, S., and García Rozas, J. R, Injective representations of infinite quivers. Applications. Canad. J. Math. 61(2009), no. 2, 315–335.http://dx.doi.org/10.4153/CJM-2009-016-2 Google Scholar
[EEO] Enochs, E., Estrada, S., and Øzdemir, S., Transfinite tree quivers and their representations. Math. Scand. 112(2013), no. 1, 49–60.Google Scholar
[EGOP] Enochs, E., García Rozas, J. R., Oyonarte, L., and Park, S., Noetherian quivers. Quaest. Math. 25(2002), no. 4, 531–538.http://dx.doi.org/10.2989/16073600209486037 Google Scholar
[EH] Enochs, E. and Herzog, I., A homotopy of quiver morphisms with applications to representations. Canad. J. Math. 51(1999), no. 2, 294–308.http://dx.doi.org/10.4153/CJM-1999-015-0 Google Scholar
[EOT] Enochs, E., Oyonarte, L., and Torrecillas, B., Flat covers and flat representations of quivers. Comm. Algebra 32(2004), no. 4, 1319–1338. http://dx.doi.org/10.1081/AGB-120028784 Google Scholar
[EHS] Eshraghi, H., Hafezi, R., and Salarian, Sh., Total acyclicity for complexes of representations of quivers. Comm. Algebra 41(2013), no. 12, 4425–4441. http://dx.doi.org/10.1080/00927872.2012.701682 Google Scholar
[E] Estrada, S., Monomial algebras over infinite quivers. Applications to N-complexes of modules. Comm. Algebra 35(2007), no. 10, 3214–3225.http://dx.doi.org/10.1080/00914030701410211 Google Scholar
[GH] Gillespie, J. and Hovey, M., Gorenstein model structures and generalized derived categories. Proc.Edinb. Math. Soc. (2) 53(2010), no. 3, 675–696. http://dx.doi.org/10.1017/S0013091508000709 Google Scholar
[Hap] Happel, D., Triangulated categories in the representation theory of finite dimensional algebras. London Mathematical Society Lecture Note Series, 119, Cambridge University Press, Cambridge,1988.Google Scholar
[HR1] Happel, D. and Ringel, C. M., Tilted algebras. Trans. Amer. Math. Soc. 274(1982), no. 2, 399–443.http://dx.doi.org/10.1090/S0002-9947-1982-0675063-2 Google Scholar
[Har] Hartshorne, R., Residues and duality. Lecture notes of a seminar on the work of A. Grothendieck,given at Harvard 1963/64. Lecture Notes in Mathematics, 20, Springer-Verlag, Berlin-New York, 1966.Google Scholar
[HR2] Höinghaus, D. and Richter, G., Hilbert basis quivers. Proceedings of the Symposium on Categorical Algebra and Topology (Cape Town, 1981). Quaestiones Math. 6(1983), no. 1–3, 157–175.http://dx.doi.org/10.1080/16073606.1983.9632298 Google Scholar
[IK] Iyengar, S. and Krause, H., Acyclicity versus total acyclicity for complexes over noetherian rings. Doc. Math. 11(2006), 207–240.Google Scholar
[J] Jörgensen, P., The homotopy category of complexes of projective modules. Adv. Math. 193(2005), no. 1, 223–232.http://dx.doi.org/10.1016/j.aim.2004.05.003 Google Scholar
[K05] Krause, H., The stable derived category of a noetherian scheme. Compos. Math. 141(2005), no. 5, 1128–1162. http://dx.doi.org/10.1112/S0010437X05001375 Google Scholar
[K08] Krause, H., Representations of quivers via reflection functors. http://www2.math.uni-paderborn.de/people/henning-krause.html Google Scholar
[K12] Krause, H., Approximations and adjoints in homotopy categories. Math. Ann. 353(2012), no. 3, 765–781. http://dx.doi.org/10.1007/s00208-011-0703-y Google Scholar
[M] Murfet, D., The mock homotopy category of projectives and Grothendieck duality. Ph.D. thesis, 2007.Google Scholar
[N08] Neeman, A., The homotopy category of flat modules, and Grothendieck duality. Invent. Math. 174(2008), no. 2, 255–308. http://dx.doi.org/10.1007/s00222-008-0131-0 Google Scholar
[PS] Peskine, C. and Szpiro, L., Dimension projective finie et cohomologie locale. Application à la démonstration de conjectures de M. Auslander, H. Bass et A. Grothendieck. Inst. Hautes Études Sci. Publ. Math. 42(1973), 47–119.Google Scholar
[RV] Reiten, I. and Van den Bergh, M., Noetherian hereditary abelian categories satisfying Serre duality. J. Amer. Math. Soc. 15(2002), no. 2, 295–366. http://dx.doi.org/10.1090/S0894-0347-02-00387-9 Google Scholar
[Ric] Rickard, J., Morita theory for derived category. J. Lond. Math. Soc. (2) 39(1989), no. 3, 436–456.http://dx.doi.org/10.1112/jlms/s2-39.3.436 Google Scholar
[Ri] Ringel, C. M., The regular components of the Auslander-Reiten quiver of a tilted algebra. Chin. Ann. Math. 9(1988), 1–18.Google Scholar
[Ro] Roberts, P., Two applications of dualizing complexes over local rings. Ann. Sci. Éc. Norm. Sup. 9(1976), no. 1, 103–106.Google Scholar
[Ru] Rump, W., Injective tree representations. J. Pure Appl. Algebra 217(2013), no. 1, 132–136.http://dx.doi.org/10.1016/j.jpaa.2012.06.018 Google Scholar