Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-18T11:04:03.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Besov Spaces and Hausdorff Dimension For Some Carnot-Carathéodory Metric Spaces

Published online by Cambridge University Press:  20 November 2018

Leszek Skrzypczak
Leszek Skrzypczak*
Affiliation:
Faculty of Mathematics and Computer Science, A. Mickiewicz University, Umultowska 871, 61-614 Poznán, Poland, e-mail: lskrzyp@amu.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

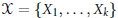We regard a system of left invariant vector fields $X=\,\{{{X}_{1}},\,\ldots ,\,{{X}_{k}}\}$ satisfying the Hörmander condition and the related Carnot-Carathéodory metric on a unimodular Lie group 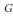$G$. We define Besov spaces corresponding to the sub-Laplacian 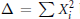$\Delta \,=\,\sum X_{i}^{2}$ both with positive and negative smoothness. The atomic decomposition of the spaces is given. In consequence we get the distributional characterization of the Hausdorff dimension of Borel subsets with the Haar measure zero.

Keywords

46E3543A1528A78Besov spacessub-elliptic operatorsCarnot-Carathéodory metricHausdorff dimension
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 6 , 01 December 2002 , pp. 1280 - 1304
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Coifman, R. R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes. Lecture Notes Math. 242, Springer-Verlag, 1971.Google Scholar
[2] Coulhon, T. and Saloff-Coste, L., Semi-groupes d'opérateurs et espaces fonctionels sur les groupes de Lie. J. Approx. Theory 65 (1991), 176–198.Google Scholar
[3] Coulhon, T. and Saloff-Coste, L., Théorèmes de Sobolev pour les semi-groupes d'opérateurs et application aux groupes de Lie unimodulaires. C. R. Acad. Sci. Paris 309 (1989), 289–294.Google Scholar
[4] Danielli, D., Garofalo, N. and Nhieu, D.-M., Trace inequalities for Carnot-Carath´odory spaces and Applications. Ann. Scuola Norm. Sup. Pisa 27 (1998), 195–252.Google Scholar
[5] ter Elst, A. F. M. and Robinson, D. W., Subelliptic operators on Lie Groups: Regularity. J. Austral. Math. Soc. 57 (1994), 179–229.Google Scholar
[6] Falconer, K. J., The geometry of fractal sets. Cambridge Univ. Press, 1985.Google Scholar
[7] Folland, G. B., Subelliptic estimates and function spaces on nilpotent Lie groups, Ark. Mat. 13 (1975), 161–207.Google Scholar
[8] Folland, G. B., Lipschitz classes and Poisson integrals on stratified groups, Studia Math. 64 (1979), 37–55.Google Scholar
[9] Frazier, M. and Jawerth, B., Decomposition of Besov spaces. Indiana Univ.Math J. 34 (1985), 777–799.Google Scholar
[10] Frazier, M. and Jawerth, B., A discrete transform and decomposition of distribution spaces. J. Funct. Anal. 93 (1990), 34–170.Google Scholar
[11] Hutchinson, J. E., Fractals and self-similarity. Indiana Univ.Math. J. 30 (1981), 713–747.Google Scholar
[12] Maćàs, R. A. and Segovia, C., A decomposition into atoms of distributions on spaces of homogeneous type. Adv. in Math. 33 (1979), 271–309.Google Scholar
[13] Mattila, P., Geometry of Sets and Measures in Euclidean spaces. Cambridge Univ. Press, 1995.Google Scholar
[14] Mitchel, J., On Carnot-Carathéodory metrics. J. Differential Geom. 21 (1985), 35–45.Google Scholar
[15] Robinson, D. W., Elliptic operators and Lie Groups. Oxford Univ. Press, 1991.Google Scholar
[16] Saka, K., Besov spaces and Sobolev spaces on a nilpotent Lie group. T.ohoku Math. J. 31 (1979), 383–437.Google Scholar
[17] Saloff-Coste, L., Parabolic Harnack inequality for divergence form second order differential operators. Potential Anal. 4 (1995), 429–467.Google Scholar
[18] Skrzypczak, L., Heat and harmonic extensions for function spaces of Hardy-Sobolev-Besov type on symmetric spaces and Lie groups. J. Approx. Theory 96 (1999), 149–170.Google Scholar
[19] Skrzypczak, L., The atomic decomposition on manifolds with bounded geometry. Forum Math. 10 (1998), 19–38.Google Scholar
[20] Stein, E., Harmonic Analysis. Real-variable methods, orthogonality, and oscillatory integrals. Princeton Univ. Press, 1993.Google Scholar
[21] Stein, E., Singular Integrals and Differential Properties of Functions. Princeton Univ. Press, 1970.Google Scholar
[22] Strichartz, R. S., Analysis of the Laplacian on a complete Riemannian manifold. J. Funct. Anal. 52 (1983), 48–79.Google Scholar
[23] Strichartz, R. S., Self-similarity on Nilpotent Lie Groups. Contemp.Math. 140, 123–157.Google Scholar
[24] Strichartz, R. S., Sub-Riemannian geometry. J. Differential Geom. 24 (1986), 221–263.Google Scholar
[25] Triebel, H., Fractals and Spectra. Birkhäuser, Verlag, 1997.Google Scholar
[26] Triebel, H., Theory of Function Spaces II. Birkhäuser, Verlag, 1992.Google Scholar
[27] Triebel, H. and Winkelvoß, H., A Fourier analytical characterization of the Hausdorff dimension of a closed set and of related Lebesgue spaces. Studia Math. 112(1996), 149–166.Google Scholar
[28] Varopoulos, N. Th., Saloff-Coste, L. and Coulhon, T., Analysis and Geometry on Groups. Cambridge Univ. Press, 1992.Google Scholar