Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-5c569c448b-nqqt6 Total loading time: 0.285 Render date: 2022-07-04T07:06:05.760Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true } hasContentIssue true
  • English
Canadian Journal of Mathematics Canadian Journal of Mathematics

Article contents

Weights of the Mod p Kernels of Theta Operators

Published online by Cambridge University Press:  20 November 2018

Siegfried Böcherer ,
Toshiyuki Kikuta  and
Sho Takemori
Siegfried Böcherer
Affiliation:
Mathematisches Institut, Universität Mannheim, 68131 Mannheim, Germany e-mail: boecherer@t-online.de
Toshiyuki Kikuta
Affiliation:
Faculty of Information Engineering, Department of Information and Systems Engineering, Fukuoka Institute of Technology, 3-30-1 Wajiro-higashi, Higashi-ku, Fukuoka 811-0295, Japan e-mail: kikuta@fit.ac.jp
Sho Takemori
Affiliation:
Department of Mathematics, Hokkaido University, Kita 10, Nishi 8, Kita-Ku, Sapporo, 060-0810, Japan e-mail: takemori@math.sci.hokudai.ac.jp
Get access Rights & Permissions[Opens in a new window]

Abstract

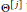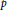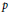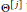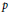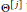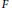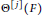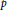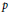Let ${{\Theta }^{[j]}}$ be an analogue of the Ramanujan theta operator for Siegel modular forms. For a given prime $p$, we give the weights of elements of mod $p$ kernel of ${{\Theta }^{[j]}}$, where the mod $p$ kernel of ${{\Theta }^{[j]}}$ is the set of all Siegel modular forms $F$ such that ${{\Theta }^{[j]}}(F)$ is congruent to zero modulo $p$. In order to construct examples of the mod $p$ kernel of 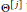${{\Theta }^{[j]}}$ from any Siegel modular forms, we introduce new operators 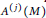${{A}^{(j)}}(M)$ and show the modularity of 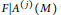$F|{{A}^{\left( j \right)}}\left( M \right)$ when 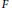$F$ is a Siegel modular form. 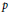Finally, we give some examples of the mod $p$ kernel of 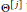${{\Theta }^{[j]}}$ and the filtrations of some of them.

Keywords

11F3311F46Siegel modular formcongruences for modular formsFourier coefficientsRamanujan's operatorfiltration
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 241 - 264
Copyright
Copyright © Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Andrianov, A. N.and Zhuravlev, V. G., Modular forms and Hecke operators. AMS Translations of Mathematical Monographs 145,1995.Google Scholar
[2] Böcherer, S., Über gewisse Siegelsche Modulformen zweiten Grades. Math. Ann. 261(1982), 23–41.http://dx.doi.Org/10.1007/BF01456406 CrossRefGoogle Scholar
[3] Böcherer, S., On the Hecke operator U(p). With an appendix by Ralf Schmidt. J. Math. Kyoto Univ. 45(2005), no. 4, 807–829. http://dx.doi.org/10.1215/kjm/1250281658 CrossRefGoogle Scholar
[4] Böcherer, S., and Kikuta, T., On modp singular modular forms. Forum Math. 28(2016), no. 6, 1051–1065.10.1515/forum-2015-0062CrossRefGoogle Scholar
[5] Böcherer, S., Kodama, H., and Nagaoka, S., On the kernel of the theta operator modp. Manuscripta Math., to appear. http://arxiv:1707.03680 Google Scholar
[6] Böcherer, S. and Nagaoka, S., On mod p properties of Siegel modular forms. Math. Ann. 338(2007), 421–433. http://dx.doi.org/10.1007/s00208-007-0081-7 CrossRefGoogle Scholar
[7] Böcherer, S. and Nagaoka, S., Congruences for Siegel modular forms and their weights. Abh. Math. Semin. Univ. Hambg. 80(2010), 227–231.http://dx.doi.Org/10.1007/s12188-010-0042-z CrossRefGoogle Scholar
[8] Böcherer, S. and Nagaoka, S., On p-adic properties ofSiegel modular forms. In: Automorphic forms. Springer Proc. Math. Stat , 115. Springer, Cham, 2014, pp. 47–66.Google Scholar
[9] Choi, D., Choie, Y., and Kikuta, T., Sturm type theorem for Siegel modular forms of genus 2 modulo p. Acta Arith. 158(2013), no. 2, 129–139.http://dx.doi.Org/10.4064/aa158-2-2 CrossRefGoogle Scholar
[10] Choi, D., Choie, Y., and Richter, O., Congruences for Siegel modular forms. Annales de l'Institut Fourier , 61(2011) no.4, 1455–1466, http://dx.doi.org/10.5802/aif.2646 CrossRefGoogle Scholar
[11] Dewar, M. and Richter, O., Ramanujan congruences for Siegel modular forms. Int. J. Number Theory 6(2010), no. 7, 1677–1687 http://dx.doi.Org/10.1142/S179304211000371X CrossRefGoogle Scholar
[12] Eichler, M. and Zagier, D., The theory of facobi forms. Progress in Mathematics , 55. Birkhäuser, Boston, 1985.Google Scholar
[13] Freitag, E., Siegekche Modulfunktionen. Grundlehren der Mathematischen Wissenschaften , 254. Springer-Verlag, Berlin, 1983.Google Scholar
[14] Ichikawa, T., Congruences between Siegel modular forms. Math. Ann. 342(2008), no. 3, 527–532. http://dx.doi.Org/10.1007/s00208-008-0245-0 CrossRefGoogle Scholar
[15] Katz, N. M., A result on modular forms in characteristic p. Modular functions of one variable, V. Lecture Notes in Math. , 601, Springer, Berlin, 1977, pp. 53–61.Google Scholar
[16] Kikuta, T., Kodama, H., and Nagaoka, S., Note on Igusa's cusp form of weight 35. Rocky Mountain J. Math. 45(2015), no. 3, 963–972.http://dx.doi.org/10.1216/RMJ-2015-45-3-963 CrossRefGoogle Scholar
[17] Kikuta, T. and Takemori, S., Sturm bounds for Siegel modular forms of degree 2 and odd weights. http://arxiv:1 508.01 610 Google Scholar
[18] Mizumoto, S., On integrality of certain algebraic numbers associated with modular forms. Math. Ann. 265(1983), no. 1, 119–135.http://dx.doi.org/10.1007/BF01456941 CrossRefGoogle Scholar
[19] Nagaoka, S., Note on mod p Siegel modular forms. Mathe Zeitschrift 235(2000), no. 2, 405–420. http://dx.doi.Org/10.1007/s002090000135 CrossRefGoogle Scholar
[20] Nagaoka, S., Note on mod p Siegel modular forms. II. Mathe Zeitschrift 251(2005), no. 4, 821–826.http://dx.doi.org/10.1007/s00209-005-0832-7 CrossRefGoogle Scholar
[21] Nagaoka, S., On the mod p kernel of the theta operator. Proc. Amer. Math. Soc. 143(2015), no. 10, 4237–4244.http://dx.doi.org/10.1090/S0002-9939-2015-12567-1 CrossRefGoogle Scholar
[22] Nagaoka, S. and Takemori, S., Notes on theta series for Niemeier lattices. Ramanujan J. 42(2017), no. 2, 385–400.http://dx.doi.Org/10.1007/s11139-015-9720-x CrossRefGoogle Scholar
[23] Serre, J.-P., Formes modulaires et fonctions zêta p-adiques. In: Modular functions of one variable, III. Lecture Notes in Math. , 350. Springer, Berlin, 1973, pp. 191–268.10.1007/978-3-540-37802-0_4CrossRefGoogle Scholar
[24] Swinnerton-Dyer, H. P. F., On l-adic representations and congruences for coefficients of modular forms. In: Modular functions of one variable, III. Lecture Notes in Math. , 350. Springer, Berlin, 1973, pp. 1–55.10.1007/978-3-540-37802-0_1CrossRefGoogle Scholar
[25] Takemori, S., Congruence relations for Siegel modular forms of weight 47, 71, and 89. Exp. Math. 23(2014), no. 4, 423–428.http://dx.doi.org/10.1080/10586458.2014.935895 CrossRefGoogle Scholar
[26] Weissauer, R., Siegel modular forms mod p. http://arxiv:0804.3134 Google Scholar
[27] Weissauer, R., Vektorwertige Siegelsche Modulformen kleinen Gewichtes. J. Reine Angew. Math. 343(1983), 184–202.Google Scholar
[28] Yamauchi, T., The weight reduction of mod p Siegel modular forms for GSpn. http://arxiv:1410.7894 Google Scholar
[29] Ziegler, C., Jacobi forms of higher degree. Abh. Math. Sem. Univ. Hamburg 59(1989), 191–224. http://dx.doi.org/10.1007/BF02942329 CrossRefGoogle Scholar

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Weights of the Mod p Kernels of Theta Operators
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Weights of the Mod p Kernels of Theta Operators
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Weights of the Mod p Kernels of Theta Operators
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *