Article contents
On Restriction Estimates for the Zero Radius Sphere over Finite Fields
Published online by Cambridge University Press: 27 February 2020
Abstract
In this paper, we completely solve the 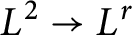 $L^{2}\to L^{r}$
extension conjecture for the zero radius sphere over finite fields. We also obtain the sharp
$L^{2}\to L^{r}$
extension conjecture for the zero radius sphere over finite fields. We also obtain the sharp 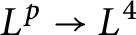 $L^{p}\to L^{4}$
extension estimate for non-zero radii spheres over finite fields, which improves the previous result of the first and second authors significantly.
$L^{p}\to L^{4}$
extension estimate for non-zero radii spheres over finite fields, which improves the previous result of the first and second authors significantly.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
A. Iosevich was partially supported by the NSA Grant H98230-15-1-0319. D. Koh was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (NRF-2018R1D1A1B07044469). T. Pham was supported by Swiss National Science Foundation grant P400P2-183916. Chun-Yen Shen was supported in part by MOST through grant 108-2628-M-002-010-MY4.
References
- 8
- Cited by



