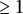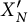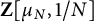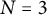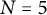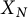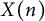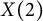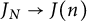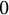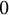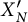1 Introduction
Let
![]() $\Gamma $
be a subgroup of finite index of
$\Gamma $
be a subgroup of finite index of
![]() ${\mathrm {SL}}_2({\mathbb {Z}})$
. This subgroup acts by homographies on the complex upper half-plane
${\mathrm {SL}}_2({\mathbb {Z}})$
. This subgroup acts by homographies on the complex upper half-plane
![]() $\mathfrak {H}$
. Consider the corresponding modular curve
$\mathfrak {H}$
. Consider the corresponding modular curve
![]() ${Y_\Gamma =\Gamma \backslash \mathfrak {H}}$
, and its compactification obtained by adding the cusps
${Y_\Gamma =\Gamma \backslash \mathfrak {H}}$
, and its compactification obtained by adding the cusps
![]() $X_\Gamma $
. We say that
$X_\Gamma $
. We say that
![]() $X_\Gamma $
satisfies the Manin–Drinfeld principle if any cuspidal (i.e., supported on the cusps) divisor of degree
$X_\Gamma $
satisfies the Manin–Drinfeld principle if any cuspidal (i.e., supported on the cusps) divisor of degree
![]() $0$
is torsion in the Jacobian of
$0$
is torsion in the Jacobian of
![]() $X_\Gamma $
. Manin and Drinfeld proved that it is the case when
$X_\Gamma $
. Manin and Drinfeld proved that it is the case when
![]() $\Gamma $
is a congruence subgroup.
$\Gamma $
is a congruence subgroup.
For a subgroup of finite index (not necessarily a congruence subgroup), K. Murty and Ramakrishnan [Reference Murty and Ramakrishnan13] give an analytic criterion for the Manin–Drinfeld principle to be satisfied. As an illustrative example, Murty and Ramakrishnan consider modular curves attached to certain subgroups of
![]() $\Gamma (2)$
: Fermat curves, and what they propose to call Heisenberg curves. We revisit those examples. In [Reference Banerjee and Merel2], we reconsider this question and give an analytic criterion of a different nature, but also based on Eisenstein series; this is unconnected to the present work, which is purely algebraic in nature.
$\Gamma (2)$
: Fermat curves, and what they propose to call Heisenberg curves. We revisit those examples. In [Reference Banerjee and Merel2], we reconsider this question and give an analytic criterion of a different nature, but also based on Eisenstein series; this is unconnected to the present work, which is purely algebraic in nature.
The Heisenberg curves are defined as follows from the complex analytic point of view. Let A and B be the classes of the matrices
 $\begin {pmatrix} 1 & 2 \\ 0 & 1 \\ \end {pmatrix}$
and
$\begin {pmatrix} 1 & 2 \\ 0 & 1 \\ \end {pmatrix}$
and
 $\begin {pmatrix} 1 & 0 \\ 2 & 1 \\ \end {pmatrix}$
, respectively, in
$\begin {pmatrix} 1 & 0 \\ 2 & 1 \\ \end {pmatrix}$
, respectively, in
![]() ${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
. These matrices generate freely the group
${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
. These matrices generate freely the group
![]() ${\bar \Gamma }(2)$
. Let
${\bar \Gamma }(2)$
. Let
![]() $C=ABA^{-1}B^{-1}$
.
$C=ABA^{-1}B^{-1}$
.
Let N be an integer
![]() $>0$
. Denote by
$>0$
. Denote by
![]() $\Phi _N$
the kernel of the morphism
$\Phi _N$
the kernel of the morphism
![]() ${{\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2}$
which to A associates
${{\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2}$
which to A associates
![]() $(1,0)$
and to B associates
$(1,0)$
and to B associates
![]() $(0,1)$
. The corresponding modular curve is the Fermat modular curve and is denoted by
$(0,1)$
. The corresponding modular curve is the Fermat modular curve and is denoted by
![]() $X_{N}$
. It can be identified with the complex points of the Fermat curve
$X_{N}$
. It can be identified with the complex points of the Fermat curve
![]() $F_N$
(see, for instance, [Reference Lang7, Reference Rohrlich17]). Let
$F_N$
(see, for instance, [Reference Lang7, Reference Rohrlich17]). Let
![]() $\Phi _N'$
be the subgroup of
$\Phi _N'$
be the subgroup of
![]() $\Phi _N$
generated by
$\Phi _N$
generated by
![]() $A^N$
,
$A^N$
,
![]() $B^N$
,
$B^N$
,
![]() $C^N$
and the third term
$C^N$
and the third term
![]() $[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
in the descending central series of
$[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
in the descending central series of
![]() ${\bar \Gamma }(2)$
. An exact sequence of groups follows:
${\bar \Gamma }(2)$
. An exact sequence of groups follows:
where
![]() $H_N$
is a central extension of
$H_N$
is a central extension of
![]() $({{\mathbb {Z}}/N{\mathbb {Z}}})^{2}$
by
$({{\mathbb {Z}}/N{\mathbb {Z}}})^{2}$
by
![]() ${{\mathbb {Z}}/N{\mathbb {Z}}}$
(coinciding with the
${{\mathbb {Z}}/N{\mathbb {Z}}}$
(coinciding with the
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
-points of the Heisenberg group). The Nth Heisenberg modular curve, in the sense of Murty and Ramakrishnan, is
${\mathbb {Z}}/N{\mathbb {Z}}$
-points of the Heisenberg group). The Nth Heisenberg modular curve, in the sense of Murty and Ramakrishnan, is
![]() $X^{\prime }_N=X_{\Phi ^{\prime }_N}$
.
$X^{\prime }_N=X_{\Phi ^{\prime }_N}$
.
Let
![]() $\mathbb {Q}(\mu _{N})$
be a cyclotomic extension of
$\mathbb {Q}(\mu _{N})$
be a cyclotomic extension of
![]() $\mathbb {Q}$
generated by Nth roots of unity. Denote by
$\mathbb {Q}$
generated by Nth roots of unity. Denote by
![]() ${\mathbb {Z}}[\mu _{N}]$
its ring of integers. The covering
${\mathbb {Z}}[\mu _{N}]$
its ring of integers. The covering
![]() $X^{\prime }_{N}\rightarrow X_{N}$
extends to a morphism
$X^{\prime }_{N}\rightarrow X_{N}$
extends to a morphism
![]() $F^{\prime }_{N}\rightarrow F_{N}$
of curves over
$F^{\prime }_{N}\rightarrow F_{N}$
of curves over
![]() $\mathbb {Q}(\mu _{N})$
that we call the Heisenberg covering of the Fermat curve.
$\mathbb {Q}(\mu _{N})$
that we call the Heisenberg covering of the Fermat curve.
Theorem 1.1 Suppose N is an odd integer. The Heisenberg modular curve
![]() $X^{\prime }_N$
extends to a smooth projective scheme
$X^{\prime }_N$
extends to a smooth projective scheme
![]() ${\mathcal {F}}^{\prime }_N$
of relative dimension one over
${\mathcal {F}}^{\prime }_N$
of relative dimension one over
![]() $\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
given by the following model:
$\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
given by the following model:
and, for every primitive Nth root of unity
![]() $\zeta $
in
$\zeta $
in
![]() $\mathbb {Q}(\mu _{N})$
$\mathbb {Q}(\mu _{N})$
 $$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j}Z)^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j}Z)^{j}U_{\zeta}^{N}. \end{align*} $$
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j}Z)^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j}Z)^{j}U_{\zeta}^{N}. \end{align*} $$
It seems to have been known to Deligne (see a comment in [Reference Murty and Ramakrishnan13]) that the generic fiber
![]() $F^{\prime }_{N}$
of
$F^{\prime }_{N}$
of
![]() ${\mathcal {F}}^{\prime }_N$
can be defined over
${\mathcal {F}}^{\prime }_N$
can be defined over
![]() ${\mathbb {Q}}$
, an assertion for which we provide a proof.
${\mathbb {Q}}$
, an assertion for which we provide a proof.
Rohrlich [Reference Rohrlich17] (see also Vélu [Reference Vélu18]) has determined the cuspidal subgroup of
![]() $F_N$
. In particular, he has shown that any cuspidal divisor on
$F_N$
. In particular, he has shown that any cuspidal divisor on
![]() $F_N$
is of order dividing N. This description plays a key role in justifying the existence of the Heisenberg covering. We show that, by going further in the descending central series of
$F_N$
is of order dividing N. This description plays a key role in justifying the existence of the Heisenberg covering. We show that, by going further in the descending central series of
![]() $\Gamma (2)$
,
$\Gamma (2)$
,
![]() $X^{\prime }_N$
is covered by a modular curve
$X^{\prime }_N$
is covered by a modular curve
![]() $X^{\prime \prime }_N$
, in such a way that
$X^{\prime \prime }_N$
, in such a way that
![]() $X^{\prime \prime }_N$
is still an abelian covering of the Fermat curve
$X^{\prime \prime }_N$
is still an abelian covering of the Fermat curve
![]() $X_{N}$
. We do not describe algebraically
$X_{N}$
. We do not describe algebraically
![]() $X^{\prime \prime }_N$
.
$X^{\prime \prime }_N$
.
We note that there has been a considerable interest in the cuspidal group of the Fermat curve. For instance, in [Reference Mazur10, p. 39], Mazur draws (or rather “stretches”) an analogy between Fermat curves and modular curves. Such an analogy is somewhat strengthened by the fact that the Heisenberg covering is analogous to the familiar Shimura covering
![]() $X_1(N)\rightarrow X_0(N)$
between modular curves.
$X_1(N)\rightarrow X_0(N)$
between modular curves.
Like Murty and Ramakrishnan, our goal had been to illustrate our study of non-congruence subgroups by examining Heisenberg curves. We can not determine in general whether such curves satisfy the Manin–Drinfeld principle. But we can show easily that the principle holds for
![]() $N=3$
. Furthermore, for
$N=3$
. Furthermore, for
![]() $N=3$
, we study the connection between
$N=3$
, we study the connection between
![]() $F^{\prime }_{3}$
and various modular curves. By contrast, we have the following theorem for
$F^{\prime }_{3}$
and various modular curves. By contrast, we have the following theorem for
![]() $N=5$
:
$N=5$
:
Theorem 1.2 There exists a cuspidal divisor on
![]() $X^{\prime }_5$
whose class in the Jacobian of
$X^{\prime }_5$
whose class in the Jacobian of
![]() $X^{\prime }_5$
is of infinite order.
$X^{\prime }_5$
is of infinite order.
Let
![]() $\bar \Gamma '(2)$
be the subgroup of index
$\bar \Gamma '(2)$
be the subgroup of index
![]() $3$
of
$3$
of
![]() $\bar \Gamma (2)$
obtained by pulling back the
$\bar \Gamma (2)$
obtained by pulling back the
![]() $2$
-Sylow subgroup of
$2$
-Sylow subgroup of
![]() $\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Let
$\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Let
![]() $\Gamma $
be a congruence subgroup of
$\Gamma $
be a congruence subgroup of
![]() $\bar \Gamma (2)$
. Consider the correspondence
$\bar \Gamma (2)$
. Consider the correspondence
![]() $X^{\prime }_N\rightarrow X_\Gamma $
obtained by combining pulling back to the modular curve
$X^{\prime }_N\rightarrow X_\Gamma $
obtained by combining pulling back to the modular curve
![]() $X_{\Gamma \cap \Phi ^{\prime }_N}$
with pushing to
$X_{\Gamma \cap \Phi ^{\prime }_N}$
with pushing to
![]() $X_\Gamma $
. It produces a morphism of abelian varieties between the Jacobians or Riemann surfaces
$X_\Gamma $
. It produces a morphism of abelian varieties between the Jacobians or Riemann surfaces
![]() $\theta _{N,\Gamma }$
:
$\theta _{N,\Gamma }$
:
![]() $J^{\prime }_N\rightarrow J_\Gamma $
. In view of the following statement, we can hardly have any hope of establishing a limited form of the Manin–Drinfeld principle for Heisenberg curves using the classical Manin–Drinfeld theorem for congruence subgroups.
$J^{\prime }_N\rightarrow J_\Gamma $
. In view of the following statement, we can hardly have any hope of establishing a limited form of the Manin–Drinfeld principle for Heisenberg curves using the classical Manin–Drinfeld theorem for congruence subgroups.
Theorem 1.3 The morphism
![]() $\theta _{N,\Gamma }$
is zero if and only if either
$\theta _{N,\Gamma }$
is zero if and only if either
![]() $3 \nmid N$
or
$3 \nmid N$
or
![]() $\Gamma $
is not contained in
$\Gamma $
is not contained in
![]() $\bar \Gamma '(2)$
. If
$\bar \Gamma '(2)$
. If
![]() $3 \mid N$
and
$3 \mid N$
and
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $\bar \Gamma '(2)$
, the image of
$\bar \Gamma '(2)$
, the image of
![]() $\theta _{N,\Gamma }$
is isogenous to an elliptic curve with j-invariant
$\theta _{N,\Gamma }$
is isogenous to an elliptic curve with j-invariant
![]() $0$
. Furthermore, when
$0$
. Furthermore, when
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $\bar \Gamma '(2)$
,
$\bar \Gamma '(2)$
,
![]() $\theta _{3,\Gamma }$
has finite kernel.
$\theta _{3,\Gamma }$
has finite kernel.
The proof of Theorem 1.3 is a translation of a group theoretic statement: any term of the lower central series of
![]() $\bar \Gamma (2)$
is essentially dense in adelic completions of
$\bar \Gamma (2)$
is essentially dense in adelic completions of
![]() $\bar \Gamma (2)$
(see Proposition 2.10). In addition to these results of algebraic nature, we give a combinatorial description of the homology of the Riemann surface
$\bar \Gamma (2)$
(see Proposition 2.10). In addition to these results of algebraic nature, we give a combinatorial description of the homology of the Riemann surface
![]() $X^{\prime }_{N}$
, by a method similar to Manin’s presentation, but following the variant introduced in [Reference Merel12]. This might have an interest of its own. But it does not help us for establishing our other results.
$X^{\prime }_{N}$
, by a method similar to Manin’s presentation, but following the variant introduced in [Reference Merel12]. This might have an interest of its own. But it does not help us for establishing our other results.
One of the referees noted connections to the work of Anderson and Ihara [Reference Anderson and Ihara1], as well as unpublished computations of Deligne. We hope that all this will be made explicit in the future.
2 Heisenberg groups and the lower central series of
 $\bar \Gamma (2)$
$\bar \Gamma (2)$
2.1 The Heisenberg group
The Heisenberg group is the algebraic group of
![]() $3\times 3$
unipotent upper triangular matrices. Set:
$3\times 3$
unipotent upper triangular matrices. Set:
 $x=\begin {pmatrix} 1 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
,
$x=\begin {pmatrix} 1 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
,
 $y=\begin {pmatrix} 1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end {pmatrix}$
, and
$y=\begin {pmatrix} 1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end {pmatrix}$
, and
 $z=\begin {pmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
.
$z=\begin {pmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
.
Those elements satisfy the relations
![]() $xz=zx$
,
$xz=zx$
,
![]() $yz=zy$
, and
$yz=zy$
, and
![]() $z=xyx^{-1}y^{-1}=[x,y]$
. Thus, one obtains a presentation of the Heisenberg group over the integers. Note the formula, for a, b,
$z=xyx^{-1}y^{-1}=[x,y]$
. Thus, one obtains a presentation of the Heisenberg group over the integers. Note the formula, for a, b,
![]() $c\in \mathbf {Z},$
$c\in \mathbf {Z},$
 $$\begin{align*}x^{a}z^{b}y^{c}=\begin{pmatrix} 1 & a & b\\ 0 & 1 & c\\ 0 & 0 & 1\\ \end{pmatrix}. \end{align*}$$
$$\begin{align*}x^{a}z^{b}y^{c}=\begin{pmatrix} 1 & a & b\\ 0 & 1 & c\\ 0 & 0 & 1\\ \end{pmatrix}. \end{align*}$$
From that perspective, the group law is given by
The Heisenberg group
![]() $H_{\mathbf {Z}}$
over
$H_{\mathbf {Z}}$
over
![]() $\mathbf {Z}$
can be identified with
$\mathbf {Z}$
can be identified with
![]() $\mathbf {Z}^{3}$
with the previous group law. The abelianization of
$\mathbf {Z}^{3}$
with the previous group law. The abelianization of
![]() $H_{\mathbf {Z}}$
is freely generated by the images of x and y and is thus isomorphic to
$H_{\mathbf {Z}}$
is freely generated by the images of x and y and is thus isomorphic to
![]() $\mathbf {Z}^{2}$
. Thus,
$\mathbf {Z}^{2}$
. Thus,
![]() $H_{\mathbf {Z}}$
is a central extension of
$H_{\mathbf {Z}}$
is a central extension of
![]() $\mathbf {Z}^{2}$
by
$\mathbf {Z}^{2}$
by
![]() $\mathbf {Z}$
.
$\mathbf {Z}$
.
Let M and N be natural integers. Let L be a common divisor of M and N. Let
![]() $H_{M,N,L}$
be the quotient group of
$H_{M,N,L}$
be the quotient group of
![]() $H_{\mathbf {Z}}$
spanned by x and y with relations
$H_{\mathbf {Z}}$
spanned by x and y with relations
![]() $xz=zx$
,
$xz=zx$
,
![]() $yz=zy$
,
$yz=zy$
,
![]() $z=xyx^{-1}y^{-1}$
, and
$z=xyx^{-1}y^{-1}$
, and
![]() $x^{N}=y^{M}=z^{L}=1$
. Such a group can be identified (as a set) with
$x^{N}=y^{M}=z^{L}=1$
. Such a group can be identified (as a set) with
![]() $\mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/L\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
via the inverse of the map
$\mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/L\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
via the inverse of the map
![]() $(a,b,c)\mapsto x^{a}z^{b}y^{c}$
.
$(a,b,c)\mapsto x^{a}z^{b}y^{c}$
.
Note the map
![]() $H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
is coming from the abelianization.
$H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
is coming from the abelianization.
Let
![]() $M'$
,
$M'$
,
![]() $N'$
, and
$N'$
, and
![]() $L'$
be integer
$L'$
be integer
![]() $\ge 1$
such that
$\ge 1$
such that
![]() $M|M'$
,
$M|M'$
,
![]() $N|N'$
, and
$N|N'$
, and
![]() $L|L'$
. The canonical group homomorphism
$L|L'$
. The canonical group homomorphism
![]() $H_{M',N',L'}\rightarrow H_{M,N,L}$
is surjective. Its kernel is generated by
$H_{M',N',L'}\rightarrow H_{M,N,L}$
is surjective. Its kernel is generated by
![]() $\{x^{M},y^{N}\}$
. Since
$\{x^{M},y^{N}\}$
. Since
![]() $[x^{M},y^{N}]=z^{NM}$
, this kernel is abelian if and only if
$[x^{M},y^{N}]=z^{NM}$
, this kernel is abelian if and only if
![]() $L'|NM$
.
$L'|NM$
.
Proposition 2.1 Let T be the lower common multiple of M and N. The group
![]() $H_{M,N,L}$
is of exponent T if T is odd or
$H_{M,N,L}$
is of exponent T if T is odd or
![]() $T/L$
is even. It is of exponent
$T/L$
is even. It is of exponent
![]() $2T$
otherwise. In particular
$2T$
otherwise. In particular
![]() $H_{N,N,N}$
, for N odd, and
$H_{N,N,N}$
, for N odd, and
![]() $H_{N,N,N/2}$
, for N even, are of exponent N.
$H_{N,N,N/2}$
, for N even, are of exponent N.
Proof Let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in H_{M,N,L}$
in the subgroups generated by x and y, respectively. Let
$\beta \in H_{M,N,L}$
in the subgroups generated by x and y, respectively. Let
![]() $e=T$
if T is odd or
$e=T$
if T is odd or
![]() $T/L$
is even. Let
$T/L$
is even. Let
![]() $e=2T$
otherwise. Since
$e=2T$
otherwise. Since
![]() $[\alpha ,\beta ]$
belongs to the center of
$[\alpha ,\beta ]$
belongs to the center of
![]() $H_{M,N,L}$
, it is of order dividing L. Moreover, one has
$H_{M,N,L}$
, it is of order dividing L. Moreover, one has
![]() $(\alpha \beta )^{n}=\alpha ^{n}[\alpha ,\beta ]^{n(n-1)/2}\beta ^{n}$
, which vanishes if
$(\alpha \beta )^{n}=\alpha ^{n}[\alpha ,\beta ]^{n(n-1)/2}\beta ^{n}$
, which vanishes if
![]() $n=e$
. By this calculation, one has
$n=e$
. By this calculation, one has
![]() $(xy)^{n}=x^{n}z^{n(n-1)/2}y^{n}$
, which shows that
$(xy)^{n}=x^{n}z^{n(n-1)/2}y^{n}$
, which shows that
![]() $xy$
is of order T.
$xy$
is of order T.
Since the group
![]() ${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
is freely generated by A and B, one gets a surjective group homomorphism
${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
is freely generated by A and B, one gets a surjective group homomorphism
![]() ${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}$
which sends A and B to x and y, respectively. Its kernel is
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}$
which sends A and B to x and y, respectively. Its kernel is
![]() $[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
. Every (necessarily nilpotent) finite quotient group of
$[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
. Every (necessarily nilpotent) finite quotient group of
![]() ${\bar \Gamma }(2)$
which factorizes through
${\bar \Gamma }(2)$
which factorizes through
![]() ${\bar \Gamma }(2)/[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
is isomorphic to one of the groups
${\bar \Gamma }(2)/[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
is isomorphic to one of the groups
![]() $H_{M,N,L}$
.
$H_{M,N,L}$
.
Denote by
![]() $\Gamma _{M, N, L}$
the kernel of the map:
$\Gamma _{M, N, L}$
the kernel of the map:
![]() ${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{M,N,L}$
.
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{M,N,L}$
.
2.2 The lower central series
Recall that the lower central series
![]() $(G_k)_{k\ge 1}$
of a group G is defined recursively by
$(G_k)_{k\ge 1}$
of a group G is defined recursively by
![]() $G_1=G$
and
$G_1=G$
and
![]() $G_{k+1}=[G_k,G]$
. The quotient
$G_{k+1}=[G_k,G]$
. The quotient
![]() $G_k/G_{k+1}$
is then an abelian group. When G is a free group generated by the family
$G_k/G_{k+1}$
is then an abelian group. When G is a free group generated by the family
![]() $(t_i)_{i\in I}$
,
$(t_i)_{i\in I}$
,
![]() $G_k/G_{k+1}$
is a free abelian group generated (not freely) by the classes of the commutators of weight k on the generators, i.e., by the
$G_k/G_{k+1}$
is a free abelian group generated (not freely) by the classes of the commutators of weight k on the generators, i.e., by the
![]() $[t_{i_1},\dots ,t_{i_k}]$
, where the indices run through any sequence
$[t_{i_1},\dots ,t_{i_k}]$
, where the indices run through any sequence
![]() $\{1,2,\dots ,k\}\rightarrow I$
[Reference Hall6, Theorem 10.2.3]. When, furthermore, I is finite of cardinality m, the rank
$\{1,2,\dots ,k\}\rightarrow I$
[Reference Hall6, Theorem 10.2.3]. When, furthermore, I is finite of cardinality m, the rank
![]() $r_k$
of
$r_k$
of
![]() $G_k/G_{k+1}$
is given by Witt’s formula, involving the necklace polynomial,
$G_k/G_{k+1}$
is given by Witt’s formula, involving the necklace polynomial,
 $$ \begin{align*}r_k(G)=\frac{1}{k}\sum_{d|k}\mu(d)m^{k/d}, \end{align*} $$
$$ \begin{align*}r_k(G)=\frac{1}{k}\sum_{d|k}\mu(d)m^{k/d}, \end{align*} $$
where
![]() $\mu $
is the Möbius function. In particular, the lower central series
$\mu $
is the Möbius function. In particular, the lower central series
![]() $({\bar \Gamma }(2)_k)_{k\ge 1}$
of
$({\bar \Gamma }(2)_k)_{k\ge 1}$
of
![]() ${\bar \Gamma }(2)$
satisfies
${\bar \Gamma }(2)$
satisfies
![]() $r_1({\bar \Gamma }(2))=2$
,
$r_1({\bar \Gamma }(2))=2$
,
![]() $r_2({\bar \Gamma }(2))=1$
,
$r_2({\bar \Gamma }(2))=1$
,
![]() $r_3({\bar \Gamma }(2))=2$
, and
$r_3({\bar \Gamma }(2))=2$
, and
![]() $r_4({\bar \Gamma }(2))=3$
. The corresponding generators of
$r_4({\bar \Gamma }(2))=3$
. The corresponding generators of
![]() ${\bar \Gamma }(2)_k/{\bar \Gamma }(2)_{k+1}$
for
${\bar \Gamma }(2)_k/{\bar \Gamma }(2)_{k+1}$
for
![]() $k=1$
,
$k=1$
,
![]() $2$
,
$2$
,
![]() $3$
are the classes of
$3$
are the classes of
![]() $\{A,B\}$
,
$\{A,B\}$
,
![]() $\{C\}$
, and
$\{C\}$
, and
![]() $\{[C,A],[C,B]\}$
, respectively. Therefore, one has a surjective group morphism
$\{[C,A],[C,B]\}$
, respectively. Therefore, one has a surjective group morphism
![]() $\phi _1$
:
$\phi _1$
:
![]() ${\bar \Gamma }(2)\rightarrow {\mathbb {Z}}^2$
such that
${\bar \Gamma }(2)\rightarrow {\mathbb {Z}}^2$
such that
![]() $\phi _1(A)=(1,0)$
and
$\phi _1(A)=(1,0)$
and
![]() $\phi _1(B)=(0,1)$
. Its kernel is
$\phi _1(B)=(0,1)$
. Its kernel is
![]() ${\bar \Gamma }(2)_2$
. Moreover, one gets a group isomorphism:
${\bar \Gamma }(2)_2$
. Moreover, one gets a group isomorphism:
![]() ${\bar \Gamma }(2)_1/{\bar \Gamma }(2)_{3}\simeq H_{\mathbf {Z}}$
.
${\bar \Gamma }(2)_1/{\bar \Gamma }(2)_{3}\simeq H_{\mathbf {Z}}$
.
Next, we have the surjective group morphism
![]() $\phi _2$
:
$\phi _2$
:
![]() ${\bar \Gamma }(2)_2\rightarrow {\mathbb {Z}}$
, such that
${\bar \Gamma }(2)_2\rightarrow {\mathbb {Z}}$
, such that
![]() $\phi _2(C)=1$
. Its kernel is
$\phi _2(C)=1$
. Its kernel is
![]() ${\bar \Gamma }(2)_3$
. We can now describe
${\bar \Gamma }(2)_3$
. We can now describe
![]() $\phi _3$
:
$\phi _3$
:
![]() ${\bar \Gamma }(2)_3\rightarrow {\mathbb {Z}}^2$
such that
${\bar \Gamma }(2)_3\rightarrow {\mathbb {Z}}^2$
such that
![]() $\phi _3([C,A])=(1,0)$
and
$\phi _3([C,A])=(1,0)$
and
![]() $\phi _3([C,B])=(0,1)$
. Something interesting happens at that stage.
$\phi _3([C,B])=(0,1)$
. Something interesting happens at that stage.
For k integer
![]() $\ge 2$
, the extension
$\ge 2$
, the extension
![]() $1\rightarrow G_{k}/G_{k+1}\rightarrow G_{k-1}/G_{k+1}\rightarrow G_{k-1}/G_k\rightarrow 1$
is central. Consequently, since
$1\rightarrow G_{k}/G_{k+1}\rightarrow G_{k-1}/G_{k+1}\rightarrow G_{k-1}/G_k\rightarrow 1$
is central. Consequently, since
![]() $r_2({\bar \Gamma }(2))=1$
, the group
$r_2({\bar \Gamma }(2))=1$
, the group
![]() ${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
is abelian, and free of rank
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
is abelian, and free of rank
![]() $3$
. Of course, the extension
$3$
. Of course, the extension
![]() $1\rightarrow {\bar \Gamma }(2)_{2}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_2\rightarrow 1$
is not central.
$1\rightarrow {\bar \Gamma }(2)_{2}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_2\rightarrow 1$
is not central.
Proposition 2.2 There exists a group isomorphism
![]() $\psi $
:
$\psi $
:
![]() ${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4\simeq {\mathbb {Z}}^3$
given by
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4\simeq {\mathbb {Z}}^3$
given by
![]() $C\mapsto (0,0,1)$
,
$C\mapsto (0,0,1)$
,
![]() $[C,A]\mapsto (1,0,0)$
, and
$[C,A]\mapsto (1,0,0)$
, and
![]() $[C,B]\mapsto (0,1,0)$
. One has, for
$[C,B]\mapsto (0,1,0)$
. One has, for
![]() $\gamma \in {\bar \Gamma }(2)$
and
$\gamma \in {\bar \Gamma }(2)$
and
![]() $\delta \in \bar \Gamma (2)_2$
, the formula
$\delta \in \bar \Gamma (2)_2$
, the formula
or equivalently
In particular, one has, for i,
![]() $j\in {\mathbb {Z}}$
, the formula
$j\in {\mathbb {Z}}$
, the formula
![]() $\psi (A^iB^jC^kB^{-j}A^{-i})=(-ki,-kj,k)$
.
$\psi (A^iB^jC^kB^{-j}A^{-i})=(-ki,-kj,k)$
.
Proof Given that
![]() $\{[C,A],[C,B]\}$
is basis of the
$\{[C,A],[C,B]\}$
is basis of the
![]() ${\mathbb {Z}}$
-module
${\mathbb {Z}}$
-module
![]() ${\bar \Gamma }(2)_3/{\bar \Gamma }(2)_4$
, and C is a basis of the
${\bar \Gamma }(2)_3/{\bar \Gamma }(2)_4$
, and C is a basis of the
![]() ${\mathbb {Z}}$
module
${\mathbb {Z}}$
module
![]() ${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_3$
, any lifting of C modulo
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_3$
, any lifting of C modulo
![]() ${\bar \Gamma }(2)_3$
, to a class
${\bar \Gamma }(2)_3$
, to a class
![]() $C'$
modulo
$C'$
modulo
![]() ${\bar \Gamma }(2)_4$
gives a basis
${\bar \Gamma }(2)_4$
gives a basis
![]() $\{[C,A],[C,B], C'\}$
of
$\{[C,A],[C,B], C'\}$
of
![]() ${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
. The choice
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
. The choice
![]() $C=C'$
is evidently suitable, but is somewhat arbitrary.
$C=C'$
is evidently suitable, but is somewhat arbitrary.
One has
Since
![]() $\delta C^{-\phi _2(\delta )}\in \bar \Gamma (2)_3$
, the factor
$\delta C^{-\phi _2(\delta )}\in \bar \Gamma (2)_3$
, the factor
![]() $\gamma \delta C^{-\phi _2(\delta )}\gamma ^{-1}C^{\phi _2(\delta )}\delta ^{-1}$
belongs to
$\gamma \delta C^{-\phi _2(\delta )}\gamma ^{-1}C^{\phi _2(\delta )}\delta ^{-1}$
belongs to
![]() $\bar \Gamma (2)_4$
; hence its image by
$\bar \Gamma (2)_4$
; hence its image by
![]() $\psi $
vanishes. So we get
$\psi $
vanishes. So we get
which translates into
It remains to determine
![]() $\psi ([C,\gamma ])$
. Let
$\psi ([C,\gamma ])$
. Let
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2\in {\bar \Gamma }(2)$
. One has
$\gamma _2\in {\bar \Gamma }(2)$
. One has
Since
![]() $[\gamma _2,[\gamma _1,\delta ]]$
is a commutator of degree
$[\gamma _2,[\gamma _1,\delta ]]$
is a commutator of degree
![]() $4$
, it is in the kernel of
$4$
, it is in the kernel of
![]() $\psi $
. It follows that the map
$\psi $
. It follows that the map
![]() $\gamma \mapsto \psi (\gamma \delta \gamma ^{-1})$
is a group homomorphism from
$\gamma \mapsto \psi (\gamma \delta \gamma ^{-1})$
is a group homomorphism from
![]() $\bar \Gamma (2)$
to
$\bar \Gamma (2)$
to
![]() ${\mathbb {Z}}^2$
. For
${\mathbb {Z}}^2$
. For
![]() $\delta =C$
,
$\delta =C$
,
![]() $\gamma =A$
(resp.
$\gamma =A$
(resp.
![]() $\gamma =B$
), one has
$\gamma =B$
), one has
![]() $\psi (\gamma \delta \gamma ^{-1})=-(\psi _1(\gamma ),0)$
, hence the latter equality is true for all
$\psi (\gamma \delta \gamma ^{-1})=-(\psi _1(\gamma ),0)$
, hence the latter equality is true for all
![]() $\gamma \in \bar \Gamma (2)$
. Thus, one gets
$\gamma \in \bar \Gamma (2)$
. Thus, one gets
which gives the main formula. It remains to apply this to
![]() $\gamma =A^iB^j$
and
$\gamma =A^iB^j$
and
![]() $\delta =C^k$
to obtain the final formula.
$\delta =C^k$
to obtain the final formula.
The exact sequence
![]() $1\rightarrow {\bar \Gamma }(2)_{3}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_3\rightarrow 1$
identifies to a central group extension
$1\rightarrow {\bar \Gamma }(2)_{3}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_3\rightarrow 1$
identifies to a central group extension
2.3 The groups
 $\Phi _N$
,
$\Phi _N$
,
 $\Phi ^{\prime }_N$
, and
$\Phi ^{\prime }_N$
, and
 $\Phi ^{\prime \prime }_N$
$\Phi ^{\prime \prime }_N$
We denote the group
![]() $\Gamma _{N,N,1}$
by
$\Gamma _{N,N,1}$
by
![]() $\Phi _N$
. It is the kernel of the group homomorphism
$\Phi _N$
. It is the kernel of the group homomorphism
![]() $\bar \phi _1$
:
$\bar \phi _1$
:
![]() ${\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2$
, which maps A to
${\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2$
, which maps A to
![]() $(1,0)$
and B to
$(1,0)$
and B to
![]() $(0,1)$
(and thus C to
$(0,1)$
(and thus C to
![]() $(0,0)$
). A system of representatives for the cosets
$(0,0)$
). A system of representatives for the cosets
![]() $\Phi _N \backslash {\bar \Gamma }(2)$
is given by
$\Phi _N \backslash {\bar \Gamma }(2)$
is given by
![]() $A^i B^j$
with
$A^i B^j$
with
![]() $i,j \in \{0,1\dots (N-1)\}$
. The structure of
$i,j \in \{0,1\dots (N-1)\}$
. The structure of
![]() $\Phi _N$
is probably well-known, but we could not find a complete reference for a presentation
$\Phi _N$
is probably well-known, but we could not find a complete reference for a presentation
![]() $\Phi _N$
.
$\Phi _N$
.
Proposition 2.3 The group
![]() $\Phi _N$
is generated by
$\Phi _N$
is generated by
![]() $U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
. Moreover,
$U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
. Moreover,
![]() $\Phi _N$
has presentation
$\Phi _N$
has presentation
 $$\begin{align*}<A^N, B^N, T_{i,j}, 0\le i,j\le N-1 |[A^N,B^N]=\prod\limits_{i=0}^{N-1}\prod\limits_{j=0}^{N-1}T_{N-1-i,j}>. \end{align*}$$
$$\begin{align*}<A^N, B^N, T_{i,j}, 0\le i,j\le N-1 |[A^N,B^N]=\prod\limits_{i=0}^{N-1}\prod\limits_{j=0}^{N-1}T_{N-1-i,j}>. \end{align*}$$
Proof The group
![]() $\Phi _N$
is generated by
$\Phi _N$
is generated by
![]() $U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
(see [Reference Lang7, Reference Rohrlich17]). By the Nielsen–Schreier theorem,
$U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
(see [Reference Lang7, Reference Rohrlich17]). By the Nielsen–Schreier theorem,
![]() $\Phi _N$
, being a free subgroup of index
$\Phi _N$
, being a free subgroup of index
![]() $N^2$
of a free group on two generators, is free on
$N^2$
of a free group on two generators, is free on
![]() $N^2+1$
generators. A relation between the
$N^2+1$
generators. A relation between the
![]() $N^2+2$
exhibited generators in U presents itself:
$N^2+2$
exhibited generators in U presents itself:
 $$ \begin{align} A^NB^NA^{-N}B^{-N}=\prod_{i=0}^{N-1}\prod_{j=0}^{N-1}A^{N-1-i}B^jCB^{-j}A^{i+1-N}. \end{align} $$
$$ \begin{align} A^NB^NA^{-N}B^{-N}=\prod_{i=0}^{N-1}\prod_{j=0}^{N-1}A^{N-1-i}B^jCB^{-j}A^{i+1-N}. \end{align} $$
One of the exhibited generators in U can be expressed in terms of the
![]() $N^2+1$
remaining elements of U. Thus, we get a presentation by generators and relations of
$N^2+1$
remaining elements of U. Thus, we get a presentation by generators and relations of
![]() $\Phi _N$
.
$\Phi _N$
.
Set
![]() $N'=N$
if N is odd, and
$N'=N$
if N is odd, and
![]() $N'=N/2$
if N is even.
$N'=N/2$
if N is even.
We set
![]() $\Phi ^{\prime }_N=\Gamma _{N,N,N'}$
. It is the subgroup of
$\Phi ^{\prime }_N=\Gamma _{N,N,N'}$
. It is the subgroup of
![]() $\Phi _N$
obtained as the kernel of the morphism
$\Phi _N$
obtained as the kernel of the morphism
![]() $\bar \phi _2$
:
$\bar \phi _2$
:
![]() $\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
which vanishes on
$\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
which vanishes on
![]() $A^N$
and
$A^N$
and
![]() $B^N$
and takes the value
$B^N$
and takes the value
![]() $1$
on
$1$
on
![]() $A^iB^jCB^{-j}A^{-i}$
for i, j integers.
$A^iB^jCB^{-j}A^{-i}$
for i, j integers.
Alternately,
![]() $\Phi ^{\prime }_N$
is the kernel of the composed map
$\Phi ^{\prime }_N$
is the kernel of the composed map
![]() ${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{N,N,N'}$
. Thus, the composed map
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{N,N,N'}$
. Thus, the composed map
![]() $[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
extends to a map
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
extends to a map
![]() $\bar \phi _2$
:
$\bar \phi _2$
:
![]() $\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
, with kernel
$\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
, with kernel
![]() $\Phi ^{\prime }_N$
. It vanishes on
$\Phi ^{\prime }_N$
. It vanishes on
![]() $A^N$
and
$A^N$
and
![]() $B^N$
.
$B^N$
.
Proposition 2.4 The composed map
![]() $[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^3$
extends to a group homomorphism
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^3$
extends to a group homomorphism
which vanishes on
![]() $A^N$
and
$A^N$
and
![]() $B^N$
and, for
$B^N$
and, for
![]() $\gamma \in \bar \Gamma (2)$
and
$\gamma \in \bar \Gamma (2)$
and
![]() $\delta \in \Phi _N$
, satisfies
$\delta \in \Phi _N$
, satisfies
In particular, for i, j,
![]() $k\in {\mathbb {Z}}$
, one has
$k\in {\mathbb {Z}}$
, one has
Proof It follows from the presentation of
![]() $\Phi _N$
that formula 2.5 defines a morphism
$\Phi _N$
that formula 2.5 defines a morphism
![]() $\Phi _N\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
(it vanishes on the exhibited relation 2.3 between the generators). Such a morphism coincides with the composed map
$\Phi _N\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
(it vanishes on the exhibited relation 2.3 between the generators). Such a morphism coincides with the composed map
![]() $[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
, by the formula we established on
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
, by the formula we established on
![]() $\psi $
.
$\psi $
.
The formula 2.4 is valid whenever
![]() $\delta \in \bar \Gamma (2)_2$
, by 2.1. Since
$\delta \in \bar \Gamma (2)_2$
, by 2.1. Since
![]() $\Phi _N$
is generated by
$\Phi _N$
is generated by
![]() $\bar \Gamma (2)_2$
together with
$\bar \Gamma (2)_2$
together with
![]() $A^N$
and
$A^N$
and
![]() $B^N$
, it remains to prove 2.4 for
$B^N$
, it remains to prove 2.4 for
![]() $\delta =A^N$
and
$\delta =A^N$
and
![]() $\delta =B^N$
. Consider the case
$\delta =B^N$
. Consider the case
![]() $\delta =B^N$
for instance (the other case is similar). Let us use the formula 2.2 again. We get, for
$\delta =B^N$
for instance (the other case is similar). Let us use the formula 2.2 again. We get, for
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\gamma _2\in \bar \Gamma (2)$
, (leaving out opposite terms)
$\gamma _2\in \bar \Gamma (2)$
, (leaving out opposite terms)
We have
![]() $\bar \psi (B^N)=0$
, and
$\bar \psi (B^N)=0$
, and
![]() $\bar \psi ([\gamma _2,[\gamma _1,B^N]])$
is the reduction modulo N of
$\bar \psi ([\gamma _2,[\gamma _1,B^N]])$
is the reduction modulo N of
![]() $\psi ([\gamma _2,[\gamma _1,B^N]])$
. One has
$\psi ([\gamma _2,[\gamma _1,B^N]])$
. One has
![]() $\psi ([\gamma _2,[\gamma _1,B^N]])=-(\phi _1(\gamma _2)\phi _2([\gamma _1,B^N],0)$
. But
$\psi ([\gamma _2,[\gamma _1,B^N]])=-(\phi _1(\gamma _2)\phi _2([\gamma _1,B^N],0)$
. But
![]() $\phi _2([\gamma _1,B^N])\in N{\mathbb {Z}}$
. So we have proved that the map
$\phi _2([\gamma _1,B^N])\in N{\mathbb {Z}}$
. So we have proved that the map
![]() $\gamma \mapsto \bar \psi (\gamma B^N\gamma ^{-1})$
is a group homomorphism. It remains to prove that the formula 2.4 holds for
$\gamma \mapsto \bar \psi (\gamma B^N\gamma ^{-1})$
is a group homomorphism. It remains to prove that the formula 2.4 holds for
![]() $\gamma =A$
and
$\gamma =A$
and
![]() $\gamma =B$
(still in the configuration where
$\gamma =B$
(still in the configuration where
![]() $\delta =B^N$
). Only the case
$\delta =B^N$
). Only the case
![]() $\gamma =A$
is of interest. We have
$\gamma =A$
is of interest. We have
As
![]() $AB^NA^{-1}B^{-N}\in \bar \Gamma (2)_2$
,
$AB^NA^{-1}B^{-N}\in \bar \Gamma (2)_2$
,
![]() $\bar \psi (AB^NA^{-1}B^{-N})$
is the reduction modulo N of
$\bar \psi (AB^NA^{-1}B^{-N})$
is the reduction modulo N of
![]() $\psi (AB^NA^{-1}B^{-N})$
. We use the identity
$\psi (AB^NA^{-1}B^{-N})$
. We use the identity
The right-hand side is a product of generators of
![]() $\Phi _N$
. We can apply 2.5
$\Phi _N$
. We can apply 2.5
 $$ \begin{align*}\psi(AB^NA^{-1}B^{-N})=\sum_{i=0}^{N-1}\psi(B^iCB^{-i})=\sum_{i=0}^{N-1}(0,-i,0)=(0,N(N-1)/2,0). \end{align*} $$
$$ \begin{align*}\psi(AB^NA^{-1}B^{-N})=\sum_{i=0}^{N-1}\psi(B^iCB^{-i})=\sum_{i=0}^{N-1}(0,-i,0)=(0,N(N-1)/2,0). \end{align*} $$
Since
![]() $N'=\mathrm {gcd}(N,N(N-1)/2)$
, we have indeed that
$N'=\mathrm {gcd}(N,N(N-1)/2)$
, we have indeed that
![]() $\bar \psi (AB^NA^{-1}B^{-N})=0$
.
$\bar \psi (AB^NA^{-1}B^{-N})=0$
.
Remark 2.5 Let
![]() $N"=N'$
if N is prime to
$N"=N'$
if N is prime to
![]() $3$
, and
$3$
, and
![]() $N"=N'/3$
otherwise. The appearance of the denominator
$N"=N'/3$
otherwise. The appearance of the denominator
![]() $2$
(for
$2$
(for
![]() $N'$
) and now
$N'$
) and now
![]() $3$
(for
$3$
(for
![]() $N"$
) is related to Bernoulli numbers. We suspect that ultimately it is related to the mixed Tate motives that have been discovered by Deligne in his study of the nilpotent completion of the fundamental group of the projective line deprived of three points [Reference Deligne, Ihara, Ribet and Serre4].
$N"$
) is related to Bernoulli numbers. We suspect that ultimately it is related to the mixed Tate motives that have been discovered by Deligne in his study of the nilpotent completion of the fundamental group of the projective line deprived of three points [Reference Deligne, Ihara, Ribet and Serre4].
We define
![]() $\Phi ^{\prime \prime }_N$
as the kernel of the composed map
$\Phi ^{\prime \prime }_N$
as the kernel of the composed map
![]() $\Phi _{N}\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})\rightarrow ({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
$\Phi _{N}\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})\rightarrow ({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
Corollary 2.6 The exact sequence
makes of the group
![]() ${\bar \Gamma }(2)/\Phi _N"$
a central extension of the Heisenberg group
${\bar \Gamma }(2)/\Phi _N"$
a central extension of the Heisenberg group
![]() $H_{N,N,N'}$
by
$H_{N,N,N'}$
by
![]() $({\mathbb {Z}}/N"{\mathbb {Z}})^2$
.
$({\mathbb {Z}}/N"{\mathbb {Z}})^2$
.
Proof It follows from formula 2.4, as
![]() $\bar \phi _2$
vanishes on
$\bar \phi _2$
vanishes on
![]() $\Phi ^{\prime }_N$
.
$\Phi ^{\prime }_N$
.
We denote by
![]() $H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
the group
$H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
the group
![]() ${\bar \Gamma }(2)/\Phi _N"$
.
${\bar \Gamma }(2)/\Phi _N"$
.
Proposition 2.7 The group
![]() $H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
is of exponent N. In other words, for every
$H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
is of exponent N. In other words, for every
![]() $\gamma \in \bar \Gamma (2)$
, one has
$\gamma \in \bar \Gamma (2)$
, one has
![]() $\gamma ^N\in \Phi ^{\prime \prime }_N$
.
$\gamma ^N\in \Phi ^{\prime \prime }_N$
.
Proof It relies on relations for commutators, that, we presume, are well-known. Let G be a group. Suppose
![]() $G_4$
is trivial. Then
$G_4$
is trivial. Then
![]() $G_3$
is contained in the center of G. Let
$G_3$
is contained in the center of G. Let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in G$
. Set
$\beta \in G$
. Set
![]() $\gamma =[\alpha ,\beta ]$
,
$\gamma =[\alpha ,\beta ]$
,
![]() $\alpha '=[\gamma ^{-1},\alpha ]$
, and
$\alpha '=[\gamma ^{-1},\alpha ]$
, and
![]() $\beta '=[\gamma ^{-1},\beta ]$
. Let
$\beta '=[\gamma ^{-1},\beta ]$
. Let
![]() $n \in \mathbb {N} \cup \{0\}$
be an integer. One has the relation
$n \in \mathbb {N} \cup \{0\}$
be an integer. One has the relation
We prove it by induction on n. Indeed, it holds for
![]() $n=0$
. Suppose it holds for some value of n. We have
$n=0$
. Suppose it holds for some value of n. We have
We use the relations
![]() $\gamma ^{-1}\beta =[\gamma ^{-1},\beta ]\beta \gamma ^{-1}=\beta ' \beta \gamma ^{-1}$
,
$\gamma ^{-1}\beta =[\gamma ^{-1},\beta ]\beta \gamma ^{-1}=\beta ' \beta \gamma ^{-1}$
,
![]() $\gamma ^{-1}\alpha =[\gamma ^{-1},\alpha ]\alpha \gamma ^{-1}=\alpha ' \alpha \gamma ^{-1}$
, and
$\gamma ^{-1}\alpha =[\gamma ^{-1},\alpha ]\alpha \gamma ^{-1}=\alpha ' \alpha \gamma ^{-1}$
, and
![]() $\beta \gamma ^{-n}=\beta ^{\prime -n} \gamma ^{-n}\beta $
. Using the fact that
$\beta \gamma ^{-n}=\beta ^{\prime -n} \gamma ^{-n}\beta $
. Using the fact that
![]() $\alpha ', \beta ' \in Z(G)$
, we get
$\alpha ', \beta ' \in Z(G)$
, we get
 $$ \begin{align*} \beta^{n+1}\alpha &= \gamma^{-1}\alpha\beta\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha' \alpha \gamma^{-1} \beta \gamma^{-n} \alpha^{\prime n} \beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha\gamma^{-n-1}\beta^{n+1}\alpha^{\prime n+1}\beta^{\prime-n-n(n-1)/2} \end{align*} $$
$$ \begin{align*} \beta^{n+1}\alpha &= \gamma^{-1}\alpha\beta\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha' \alpha \gamma^{-1} \beta \gamma^{-n} \alpha^{\prime n} \beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha\gamma^{-n-1}\beta^{n+1}\alpha^{\prime n+1}\beta^{\prime-n-n(n-1)/2} \end{align*} $$
which is the desired formula. We pass to the next step. We now claim that
We proceed again by induction on n. This is true for
![]() $n=1$
. We suppose the formula holds for a certain value of n. We get
$n=1$
. We suppose the formula holds for a certain value of n. We get
Using the formula 2.6, we get
We now use the formula
![]() $\gamma ^{-{n\choose 2} }\alpha =\alpha ^{\prime {n\choose 2}}\alpha \gamma ^{-{n\choose 2}}$
and the centrality of
$\gamma ^{-{n\choose 2} }\alpha =\alpha ^{\prime {n\choose 2}}\alpha \gamma ^{-{n\choose 2}}$
and the centrality of
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
to get
$\beta '$
to get
which establishes 2.7.
The Nth powers of both A and B belong to
![]() $\Phi ^{\prime \prime }_{N}$
(Proposition 2.4). The
$\Phi ^{\prime \prime }_{N}$
(Proposition 2.4). The
![]() $N'$
th, and therefore the
$N'$
th, and therefore the
![]() ${N\choose 2}$
, power of any commutator belongs to
${N\choose 2}$
, power of any commutator belongs to
![]() $\Phi ^{\prime \prime }_{N}$
, since
$\Phi ^{\prime \prime }_{N}$
, since
![]() $\Phi ^{\prime }_{N}$
contains
$\Phi ^{\prime }_{N}$
contains
![]() $\bar \Gamma (2)_{2}$
. Similarly, the
$\bar \Gamma (2)_{2}$
. Similarly, the
![]() $N"$
th power, and therefore the
$N"$
th power, and therefore the
![]() ${N\choose 3}$
and
${N\choose 3}$
and
![]() ${N+1\choose 3}$
powers, of an element of
${N+1\choose 3}$
powers, of an element of
![]() $\bar \Gamma (2)_{3}$
belongs to
$\bar \Gamma (2)_{3}$
belongs to
![]() $\Phi ^{\prime \prime }_{N}$
. We can combine these remarks with the formula 2.7 for
$\Phi ^{\prime \prime }_{N}$
. We can combine these remarks with the formula 2.7 for
![]() $n=N$
, to establish that, if the Nth powers of
$n=N$
, to establish that, if the Nth powers of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
both belong to
$\beta $
both belong to
![]() $\Phi ^{\prime \prime }_{N}$
, one has
$\Phi ^{\prime \prime }_{N}$
, one has
![]() $(\alpha \beta )^{N}\in \Phi ^{\prime \prime }_{N}$
. The proposition follows, since
$(\alpha \beta )^{N}\in \Phi ^{\prime \prime }_{N}$
. The proposition follows, since
![]() $\{A,B\}$
generates
$\{A,B\}$
generates
![]() $\bar \Gamma (2)$
.
$\bar \Gamma (2)$
.
Remark 2.8 Let p be prime number. Stallings introduced the lower p-central series
![]() $(S_{k})_{k\ge 1}$
as a particular case for
$(S_{k})_{k\ge 1}$
as a particular case for
![]() $N=p$
of the following construction. One has
$N=p$
of the following construction. One has
![]() ${S_1=G}$
, and, for
${S_1=G}$
, and, for
![]() $k\ge 2$
,
$k\ge 2$
,
![]() $S_{k+1}=[G,S_k](S_k)^N$
, where the latter expression is the subgroup of G generated by
$S_{k+1}=[G,S_k](S_k)^N$
, where the latter expression is the subgroup of G generated by
![]() $[G,S_k]$
and
$[G,S_k]$
and
![]() $(S_k)^N$
. Note that, when
$(S_k)^N$
. Note that, when
![]() $G= {\bar \Gamma }(2)$
, one has
$G= {\bar \Gamma }(2)$
, one has
![]() ${S_2=[{\bar \Gamma }(2),{\bar \Gamma }(2)]{\bar \Gamma }(2)^N=\Phi _N}$
and
${S_2=[{\bar \Gamma }(2),{\bar \Gamma }(2)]{\bar \Gamma }(2)^N=\Phi _N}$
and
![]() $S_3=[{\bar \Gamma }(2),\Phi _N]\Phi _N^N$
. Note that
$S_3=[{\bar \Gamma }(2),\Phi _N]\Phi _N^N$
. Note that
![]() $S_3\subset \Phi _N'\subset S_2$
. Since
$S_3\subset \Phi _N'\subset S_2$
. Since
![]() $A^N$
and
$A^N$
and
![]() $B^N$
do not belong to
$B^N$
do not belong to
![]() $S_3$
, the groups
$S_3$
, the groups
![]() $S_3$
and
$S_3$
and
![]() $\Phi ^{\prime }_N$
do not coincide.
$\Phi ^{\prime }_N$
do not coincide.
2.4 Odd adelic completions
Recall that, for
![]() $k\ge 1$
,
$k\ge 1$
,
![]() ${\bar \Gamma }(2)_k$
is the kth term in the lower central series of
${\bar \Gamma }(2)_k$
is the kth term in the lower central series of
![]() ${\bar \Gamma }(2)$
. Let
${\bar \Gamma }(2)$
. Let
 $D_3=\{\pm \mathrm {Id}, \pm \begin {pmatrix} 0 & -1 \\ 1 & 0 \\ \end {pmatrix}, \pm \begin {pmatrix} -1 & 1 \\ 1 & 1 \\ \end {pmatrix}, \pm \begin {pmatrix} 1 & 1 \\ 1 & -1 \\ \end {pmatrix}\}$
in
$D_3=\{\pm \mathrm {Id}, \pm \begin {pmatrix} 0 & -1 \\ 1 & 0 \\ \end {pmatrix}, \pm \begin {pmatrix} -1 & 1 \\ 1 & 1 \\ \end {pmatrix}, \pm \begin {pmatrix} 1 & 1 \\ 1 & -1 \\ \end {pmatrix}\}$
in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
be the index
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
be the index
![]() $3$
,
$3$
,
![]() $2$
-Sylow subgroup of
$2$
-Sylow subgroup of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. It is isomorphic to the Klein group.
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. It is isomorphic to the Klein group.
Recall that the derived subgroup of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}})$
is the projective congruence subgroup of level
$\mathrm {PSL}_{2}({\mathbb {Z}})$
is the projective congruence subgroup of level
![]() $6$
whose image in
$6$
whose image in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is
![]() $D_{3}$
, and whose image in
$D_{3}$
, and whose image in
![]() $\mathrm { PSL}_{2}({\mathbb {Z}}/2{\mathbb {Z}})$
is cyclic of order
$\mathrm { PSL}_{2}({\mathbb {Z}}/2{\mathbb {Z}})$
is cyclic of order
![]() $3$
.
$3$
.
Let
be the profinite completion of
![]() ${\mathbb {Z}}$
away from the prime
${\mathbb {Z}}$
away from the prime
![]() $2$
. Let
$2$
. Let
![]() $\hat D_{\mathrm {odd}}$
be the inverse image of
$\hat D_{\mathrm {odd}}$
be the inverse image of
![]() $D_{3}$
in
$D_{3}$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
Proposition 2.9 The image of
![]() ${\bar \Gamma }(2)_2$
in
${\bar \Gamma }(2)_2$
in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is equal to
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is equal to
![]() $D_{3}$
. For p prime,
$D_{3}$
. For p prime,
![]() $p>3$
, its image modulo p is
$p>3$
, its image modulo p is
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/p{\mathbb {Z}})$
.
$\mathrm {PSL}_{2}({\mathbb {Z}}/p{\mathbb {Z}})$
.
Proof Indeed, the images of
![]() ${\bar \Gamma }(2)$
and
${\bar \Gamma }(2)$
and
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}))$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
coincide by weak approximation. Thus,
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
coincide by weak approximation. Thus,
![]() ${\bar \Gamma }(2)_2$
modulo
${\bar \Gamma }(2)_2$
modulo
![]() $3$
coincides with the derived subgroup of
$3$
coincides with the derived subgroup of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
, which in turn is the reduction modulo
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
, which in turn is the reduction modulo
![]() $3$
of the derived subgroup of
$3$
of the derived subgroup of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}))$
. The second assertion is proved similarly.
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
. The second assertion is proved similarly.
Proposition 2.10 Let k be an integer
![]() $\ge 2$
. The closure of
$\ge 2$
. The closure of
![]() ${\bar \Gamma }(2)_k$
in
${\bar \Gamma }(2)_k$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to
![]() $\hat D_{\mathrm {odd}}$
.
$\hat D_{\mathrm {odd}}$
.
Proof We prove this first for
![]() $k=2$
. Let n be an odd integer divisible by
$k=2$
. Let n be an odd integer divisible by
![]() $3$
. Let
$3$
. Let
![]() $D_n$
be the inverse image of
$D_n$
be the inverse image of
![]() $D_{3}$
in
$D_{3}$
in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. The image of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. The image of
![]() ${\bar \Gamma }(2)_2$
modulo n coincide with the image of the derived subgroup of
${\bar \Gamma }(2)_2$
modulo n coincide with the image of the derived subgroup of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}))$
modulo n, which is a subgroup of index
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
modulo n, which is a subgroup of index
![]() $3$
of
$3$
of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Such a subgroup can only be
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Such a subgroup can only be
![]() $D_n$
. Thus, we obtain the proposition for
$D_n$
. Thus, we obtain the proposition for
![]() $k=2$
.
$k=2$
.
We prove the proposition for
![]() $k=3$
. Let
$k=3$
. Let
![]() $I_n$
be the image of
$I_n$
be the image of
![]() ${\bar \Gamma }(2)_3$
in
${\bar \Gamma }(2)_3$
in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Note that we have an exact sequence
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Note that we have an exact sequence
Since we have an exact sequence
where
![]() $\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0$
is the subgroup of
$\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0$
is the subgroup of
![]() $\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})$
made of matrices of trace
$\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})$
made of matrices of trace
![]() $0$
, the equality
$0$
, the equality
![]() $I_n=D_n$
would follow from the inclusion
$I_n=D_n$
would follow from the inclusion
![]() $1+3\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0\subset K_n$
. It remains to establish the latter inclusion. Since
$1+3\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0\subset K_n$
. It remains to establish the latter inclusion. Since
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
is equal to its derived subgroup when n is prime to
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
is equal to its derived subgroup when n is prime to
![]() $6$
, by the Chinese remainder theorem, it is enough to prove it when n is a power of
$6$
, by the Chinese remainder theorem, it is enough to prove it when n is a power of
![]() $3$
.
$3$
.
It follows from the equality
![]() $[(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0},\mathrm {SL}_2({\mathbb {Z}}_p)]=(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0}$
, valid for any prime p, and the fact that the closure of
$[(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0},\mathrm {SL}_2({\mathbb {Z}}_p)]=(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0}$
, valid for any prime p, and the fact that the closure of
![]() ${\bar \Gamma }(2)_2$
in
${\bar \Gamma }(2)_2$
in
![]() $\mathrm {PSL}_2({\mathbb {Z}}_3)$
contains
$\mathrm {PSL}_2({\mathbb {Z}}_3)$
contains
![]() $[(1+3\mathrm {M}_2({\mathbb {Z}}_3))_{0}$
.
$[(1+3\mathrm {M}_2({\mathbb {Z}}_3))_{0}$
.
The general case
![]() $k\ge 3$
of the proposition is now immediate. Indeed, since
$k\ge 3$
of the proposition is now immediate. Indeed, since
![]() ${\bar \Gamma }(2)_3$
and
${\bar \Gamma }(2)_3$
and
![]() ${\bar \Gamma }(2)_2$
have the same image modulo n, those images are the second and third, respectively, derived subgroups of
${\bar \Gamma }(2)_2$
have the same image modulo n, those images are the second and third, respectively, derived subgroups of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Thus, the lower central series of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Thus, the lower central series of
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
stabilizes to the image modulo n of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
stabilizes to the image modulo n of
![]() ${\bar \Gamma }(2)_k$
for any
${\bar \Gamma }(2)_k$
for any
![]() $k\ge 3$
.
$k\ge 3$
.
Proposition 2.11 The closure of
![]() $\Phi _{N}$
in
$\Phi _{N}$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
![]() $3$
does not divide N. It is
$3$
does not divide N. It is
![]() $\hat D_{\mathrm {odd}}$
if
$\hat D_{\mathrm {odd}}$
if
![]() $3$
divides N.
$3$
divides N.
Proof If
![]() $3$
does not divide N,
$3$
does not divide N,
![]() $\Phi _N$
contains a nonzero upper triangular matrix (for instance,
$\Phi _N$
contains a nonzero upper triangular matrix (for instance,
![]() $A^{\prime N}$
) which is not the identity modulo
$A^{\prime N}$
) which is not the identity modulo
![]() $3$
. Its closure in
$3$
. Its closure in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains a maximal proper subgroup of index
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains a maximal proper subgroup of index
![]() $3$
, namely
$3$
, namely
![]() $\hat D_{\mathrm {odd}}$
, and an element which is not in that subgroup. Therefore, the closure is
$\hat D_{\mathrm {odd}}$
, and an element which is not in that subgroup. Therefore, the closure is
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
. If
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
. If
![]() $3$
divides N, since both
$3$
divides N, since both
![]() $A^{3N}$
and
$A^{3N}$
and
![]() $B^{3N}$
vanish modulo
$B^{3N}$
vanish modulo
![]() $3$
, the images of
$3$
, the images of
![]() $\Phi _N$
and
$\Phi _N$
and
![]() ${\bar \Gamma }(2)_2$
coincide in
${\bar \Gamma }(2)_2$
coincide in
![]() $\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. Hence the result.
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. Hence the result.
Proposition 2.12 The closure of
![]() $\Phi ^{\prime }_{N}$
in
$\Phi ^{\prime }_{N}$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
![]() $3$
does not divide N. It is
$3$
does not divide N. It is
![]() $\hat D_{\mathrm {odd}}$
if
$\hat D_{\mathrm {odd}}$
if
![]() $3$
divides N.
$3$
divides N.
Proof The closure of
![]() ${\bar \Gamma }(2)_2$
and
${\bar \Gamma }(2)_2$
and
![]() ${\bar \Gamma }(2)_3$
coincide modulo n for every n divisible by
${\bar \Gamma }(2)_3$
coincide modulo n for every n divisible by
![]() $3$
, as we have just established. Thus, the closure of
$3$
, as we have just established. Thus, the closure of
![]() $\Phi ^{\prime }_N$
in
$\Phi ^{\prime }_N$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains
![]() ${\bar \Gamma }(2)_2$
. Since the group
${\bar \Gamma }(2)_2$
. Since the group
![]() $\Phi ^{\prime }_{N}$
contains the matrices
$\Phi ^{\prime }_{N}$
contains the matrices
![]() $A^N$
and
$A^N$
and
![]() $B^N$
, its closure contains
$B^N$
, its closure contains
![]() $\Phi _N$
. Thus, the closure of
$\Phi _N$
. Thus, the closure of
![]() $\Phi ^{\prime }_N$
in
$\Phi ^{\prime }_N$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to the closure of
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to the closure of
![]() $\Phi _{N}$
in
$\Phi _{N}$
in
![]() $\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
Let
![]() $\bar \Gamma '(2)=\bar \Gamma (2)\cap \hat D_{\mathrm {odd}}$
. It is a subgroup of index
$\bar \Gamma '(2)=\bar \Gamma (2)\cap \hat D_{\mathrm {odd}}$
. It is a subgroup of index
![]() $3$
of
$3$
of
![]() $\bar \Gamma (2)$
.
$\bar \Gamma (2)$
.
Corollary 2.13 Let
![]() $\Gamma $
be a congruence subgroup of
$\Gamma $
be a congruence subgroup of
![]() $\bar \Gamma (2)$
. One has
$\bar \Gamma (2)$
. One has
![]() $\Gamma \Phi ^{\prime }_N= \bar \Gamma '(2)$
if
$\Gamma \Phi ^{\prime }_N= \bar \Gamma '(2)$
if
![]() $\Gamma \subset \bar \Gamma '(2)$
and
$\Gamma \subset \bar \Gamma '(2)$
and
![]() $3$
divides N. One has
$3$
divides N. One has
![]() $\Gamma \Phi ^{\prime }_N= \bar \Gamma (2)$
otherwise.
$\Gamma \Phi ^{\prime }_N= \bar \Gamma (2)$
otherwise.
Let n be an even integer. In particular, one has
![]() $\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma (2)$
if
$\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma (2)$
if
![]() $3$
does not divide either n or N. One has
$3$
does not divide either n or N. One has
![]() $\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma '(2)$
if
$\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma '(2)$
if
![]() $3$
divides both n and N.
$3$
divides both n and N.
3 The associated Riemann surfaces
3.1 The Riemann surface
 $X_{M, N,L}$
$X_{M, N,L}$
Denote by
![]() $X_{M, N,L}$
the compactified modular curve defined by
$X_{M, N,L}$
the compactified modular curve defined by
![]() $\Gamma _{M, N, L}$
.
$\Gamma _{M, N, L}$
.
Proposition 3.1 The genus
![]() $g_{M, N,L}$
of the curve
$g_{M, N,L}$
of the curve
![]() $X_{M, N,L}$
is given by the following formulas. Denote by T the lowest common multiple of M and N. Suppose T is even and
$X_{M, N,L}$
is given by the following formulas. Denote by T the lowest common multiple of M and N. Suppose T is even and
![]() $T/L$
is odd, then one has
$T/L$
is odd, then one has
Suppose T is odd or
![]() $T/L$
is even, then one has
$T/L$
is even, then one has
Proof We use Riemann–Hurwitz formula for the morphism
![]() $X_{N,M,L}\rightarrow X(2)$
. Since
$X_{N,M,L}\rightarrow X(2)$
. Since
![]() $\Gamma (2)$
has no elliptic elements, the ramification points of this morphism reside entirely among the cusps.
$\Gamma (2)$
has no elliptic elements, the ramification points of this morphism reside entirely among the cusps.
Concerning the cusps above
![]() $0$
(resp.
$0$
(resp.
![]() $\infty $
), note that the stabilizer of the rational number
$\infty $
), note that the stabilizer of the rational number
![]() $0$
(resp.
$0$
(resp.
![]() $\infty $
) in
$\infty $
) in
![]() $P\Gamma (2)$
is generated by B (resp. A). As the morphism
$P\Gamma (2)$
is generated by B (resp. A). As the morphism
![]() $X_{N,M,L}\rightarrow X(2)$
is Galois, the ramification index is independent of the chosen cusp, and is the order of the orbit of B (resp. of A) acting on
$X_{N,M,L}\rightarrow X(2)$
is Galois, the ramification index is independent of the chosen cusp, and is the order of the orbit of B (resp. of A) acting on
![]() $\Gamma _{M,N,L}\backslash \Gamma (2)$
. This is N (resp. M) by definition of
$\Gamma _{M,N,L}\backslash \Gamma (2)$
. This is N (resp. M) by definition of
![]() $\Gamma _{M,N,L}$
. Concerning the cusps above
$\Gamma _{M,N,L}$
. Concerning the cusps above
![]() $1$
, the stabilizer in
$1$
, the stabilizer in
![]() $P\Gamma (2)$
of the rational number
$P\Gamma (2)$
of the rational number
![]() $-1$
is generated by
$-1$
is generated by
![]() $A^{-1}B$
. It remains to determine the order of
$A^{-1}B$
. It remains to determine the order of
![]() $A^{-1}B$
in
$A^{-1}B$
in
![]() $\Gamma _{M,N,L}\backslash \Gamma (2)=H_{M,N,L}$
.
$\Gamma _{M,N,L}\backslash \Gamma (2)=H_{M,N,L}$
.
The abelianization provides a map:
![]() $H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
which sends
$H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
which sends
![]() $A^{-1}B$
to
$A^{-1}B$
to
![]() $(1,-1)$
. The latter element is of order T, which leads us to examine the order of
$(1,-1)$
. The latter element is of order T, which leads us to examine the order of
![]() $(A^{-1}B)^{T}$
in
$(A^{-1}B)^{T}$
in
![]() $H_{M,N,L}$
. Denote by
$H_{M,N,L}$
. Denote by
![]() $D=[A^{-1},B]$
. It belongs to and generates the center of
$D=[A^{-1},B]$
. It belongs to and generates the center of
![]() $H_{M,N,L}$
. It is of order L. Note the formula
$H_{M,N,L}$
. It is of order L. Note the formula
![]() $A^{-1}B=DBA^{-1}$
. Thus, one has
$A^{-1}B=DBA^{-1}$
. Thus, one has
![]() $(A^{-1}B)^{T}=D^{k}A^{-T}B^{T}$
in
$(A^{-1}B)^{T}=D^{k}A^{-T}B^{T}$
in
![]() $H_{M,N,L}$
, where k is the number of factors
$H_{M,N,L}$
, where k is the number of factors
![]() $A^{-1}$
to the right of a factor B in the
$A^{-1}$
to the right of a factor B in the
![]() $(A^{-1}B)^{T}$
written as a product of
$(A^{-1}B)^{T}$
written as a product of
![]() $2T$
factors. One has
$2T$
factors. One has
![]() $k=1+2+\dots +(T-1)=T(T-1)/2$
. This is why the order of
$k=1+2+\dots +(T-1)=T(T-1)/2$
. This is why the order of
![]() $(A^{-1}B)^{T}$
is
$(A^{-1}B)^{T}$
is
![]() $1$
if L is odd or if
$1$
if L is odd or if
![]() $T/L$
is even. This order is
$T/L$
is even. This order is
![]() $2$
otherwise.
$2$
otherwise.
Thus, the ramification index e of any cusp above
![]() $1$
is equal to T if L is odd or if
$1$
is equal to T if L is odd or if
![]() $T/L$
is even. It is
$T/L$
is even. It is
![]() $2T$
otherwise. We can now apply the Riemann–Hurwitz formula for the dominant morphism
$2T$
otherwise. We can now apply the Riemann–Hurwitz formula for the dominant morphism
![]() $X_{M,N,L}\rightarrow X(2)$
:
$X_{M,N,L}\rightarrow X(2)$
:
We have
![]() $d=|H_{M,N,L}|=MNL$
. One gets
$d=|H_{M,N,L}|=MNL$
. One gets
and
The lemma follows from the calculation of e.
3.2 The Riemann surfaces
 $X_N$
,
$X_N$
,
 $X^{\prime }_N$
, and
$X^{\prime }_N$
, and
 $X^{\prime \prime }_N$
$X^{\prime \prime }_N$
All three groups
![]() $\Phi _N$
,
$\Phi _N$
,
![]() $\Phi _N'$
, and
$\Phi _N'$
, and
![]() $\Phi _N"$
act on the upper half-plane
$\Phi _N"$
act on the upper half-plane
![]() $\mathbb {H}$
. We denote, respectively, by
$\mathbb {H}$
. We denote, respectively, by
![]() $X_N$
,
$X_N$
,
![]() $X^{\prime }_N$
, and
$X^{\prime }_N$
, and
![]() $X^{\prime \prime }_N$
the corresponding completed modular curves.
$X^{\prime \prime }_N$
the corresponding completed modular curves.
Proposition 3.2 Both morphisms
![]() $X^{\prime }_N\rightarrow X_N$
and
$X^{\prime }_N\rightarrow X_N$
and
![]() $X^{\prime \prime }_N\rightarrow X^{\prime }_N$
(and therefore
$X^{\prime \prime }_N\rightarrow X^{\prime }_N$
(and therefore
![]() $X^{\prime \prime }_N\rightarrow X_N$
as well) are unramified. The covering
$X^{\prime \prime }_N\rightarrow X_N$
as well) are unramified. The covering
![]() $X^{\prime }_{N}\rightarrow X_{N}$
is cyclic of degree
$X^{\prime }_{N}\rightarrow X_{N}$
is cyclic of degree
![]() $N'$
. The covering
$N'$
. The covering
![]() ${X^{\prime \prime }_{N}\rightarrow X^{\prime }_{N}}$
is Galois with group
${X^{\prime \prime }_{N}\rightarrow X^{\prime }_{N}}$
is Galois with group
![]() $({\mathbb {Z}}/N"{\mathbb {Z}})^{2}$
. The covering
$({\mathbb {Z}}/N"{\mathbb {Z}})^{2}$
. The covering
![]() $X^{\prime \prime }_{N}\rightarrow X_{N}$
is abelian with Galois group
$X^{\prime \prime }_{N}\rightarrow X_{N}$
is abelian with Galois group
![]() $({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
$({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
Proof The first statement needs only to be established for the morphism
![]() $X^{\prime \prime }_N\rightarrow X_N$
. The ramification points can only reside at the cusps. To show that those cusps are unramified, we need only to show that their width in
$X^{\prime \prime }_N\rightarrow X_N$
. The ramification points can only reside at the cusps. To show that those cusps are unramified, we need only to show that their width in
![]() $X^{\prime \prime }_N$
is equal to their width, equal to N, in
$X^{\prime \prime }_N$
is equal to their width, equal to N, in
![]() $X_N$
. Since the covering
$X_N$
. Since the covering
![]() $X^{\prime \prime }_N\rightarrow X_1$
is Galois, the width of a cusp of
$X^{\prime \prime }_N\rightarrow X_1$
is Galois, the width of a cusp of
![]() $X_N"$
depends only on its image in the set of cusps
$X_N"$
depends only on its image in the set of cusps
![]() $\{0,1,\infty \}$
of
$\{0,1,\infty \}$
of
![]() $X_1$
. We just need to look at the order of A, B and
$X_1$
. We just need to look at the order of A, B and
![]() $A^{-1}B$
in
$A^{-1}B$
in
![]() ${\bar \Gamma }(2)/\Phi ^{\prime \prime }_N$
. All three are of order N in the latter quotient.
${\bar \Gamma }(2)/\Phi ^{\prime \prime }_N$
. All three are of order N in the latter quotient.
The other assertions follow immediately from the properties of the groups
![]() $\Phi _N$
,
$\Phi _N$
,
![]() $\Phi _N'$
, and
$\Phi _N'$
, and
![]() $\Phi _N"$
.
$\Phi _N"$
.
The Riemann surface
![]() $X_N$
is isomorphic to the Riemann surface obtained from the complex points of the Fermat curve. The covering
$X_N$
is isomorphic to the Riemann surface obtained from the complex points of the Fermat curve. The covering
![]() $X_N'\rightarrow X_N$
is obtained from what we call Heisenberg covering of the Fermat curve by passing to the complex numbers.
$X_N'\rightarrow X_N$
is obtained from what we call Heisenberg covering of the Fermat curve by passing to the complex numbers.
We obtain the genus
![]() $g_N$
and
$g_N$
and
![]() $g_N'$
of the curves
$g_N'$
of the curves
![]() $X_N$
and
$X_N$
and
![]() $X_N'$
by our formulas for the genus of
$X_N'$
by our formulas for the genus of
![]() $X_{N,M,L}$
. One has
$X_{N,M,L}$
. One has
![]() $g_N=g_{N,N,1}=(N-1)(N-2)/2$
. Furthermore, if N is odd, one has
$g_N=g_{N,N,1}=(N-1)(N-2)/2$
. Furthermore, if N is odd, one has
![]() $g^{\prime }_{N}=g_{N,N,N}=(N^{3}-3N^{2}+2)/2=(N-1)(N^2-2N-2)/2$
. If N is even, one gets
$g^{\prime }_{N}=g_{N,N,N}=(N^{3}-3N^{2}+2)/2=(N-1)(N^2-2N-2)/2$
. If N is even, one gets
![]() $g^{\prime }_{N}=g_{N,N,N'}=(2N^3-5N^2+4)/4=(N-2)(2N^2-N-2)/4$
.
$g^{\prime }_{N}=g_{N,N,N'}=(2N^3-5N^2+4)/4=(N-2)(2N^2-N-2)/4$
.
The genus of
![]() $g_N"$
of the curve
$g_N"$
of the curve
![]() $X_N"$
can be deduced from the Riemann–Hurwitz formula. Since we have a covering
$X_N"$
can be deduced from the Riemann–Hurwitz formula. Since we have a covering
![]() $X^{\prime \prime }_N\rightarrow X^{\prime }_N$
of degree
$X^{\prime \prime }_N\rightarrow X^{\prime }_N$
of degree
![]() $N^{\prime \prime 2}$
, one has
$N^{\prime \prime 2}$
, one has
The curve
![]() $X^{\prime }_{N}$
possesses
$X^{\prime }_{N}$
possesses
![]() $NN'$
cusps above each of the cusps
$NN'$
cusps above each of the cusps
![]() $0$
,
$0$
,
![]() $1$
, and
$1$
, and
![]() $\infty $
of
$\infty $
of
![]() $X(2)$
.
$X(2)$
.
3.3 Some cases of small genus
Proposition 3.3 The genus g of the curve
![]() $X_{M, N,L}$
is equal to
$X_{M, N,L}$
is equal to
![]() $0$
for the following values of
$0$
for the following values of
![]() $(N,M,L)$
, and only for those values:
$(N,M,L)$
, and only for those values:
![]() $(N,1,1)$
,
$(N,1,1)$
,
![]() $(1,M,1)$
,
$(1,M,1)$
,
![]() $(2,2,1)$
,
$(2,2,1)$
,
![]() $(2,2,2)$
.
$(2,2,2)$
.
Proof The formula just established gives:
![]() $2-2g=-L(MN-N-M-MN/e)$
. Thus,
$2-2g=-L(MN-N-M-MN/e)$
. Thus,
![]() $g=0$
implies that
$g=0$
implies that
![]() $L=1$
or
$L=1$
or
![]() $2$
.
$2$
.
If
![]() $g=0$
and
$g=0$
and
![]() $L=1$
, then one has
$L=1$
, then one has
![]() $MN-N-M-MN/e=-2$
and
$MN-N-M-MN/e=-2$
and
![]() $e=\mathrm {lcm}(M,N)$
. Thus,
$e=\mathrm {lcm}(M,N)$
. Thus,
![]() $\mathrm {gcd}(M,N)$
divides
$\mathrm {gcd}(M,N)$
divides
![]() $2$
. If
$2$
. If
![]() $\mathrm {gcd}(M,N)=1$
, then one has
$\mathrm {gcd}(M,N)=1$
, then one has
![]() $MN-N-M-1=-2$
, and thus
$MN-N-M-1=-2$
, and thus
![]() $(M-1)(N-1)=0$
that is
$(M-1)(N-1)=0$
that is
![]() $M=1$
or
$M=1$
or
![]() $N=1$
. If
$N=1$
. If
![]() $\mathrm {gcd}(M,N)=2$
, one has
$\mathrm {gcd}(M,N)=2$
, one has
![]() $MN-N-M-2=-2$
and thus
$MN-N-M-2=-2$
and thus
![]() $(M-1)(N-1)=1$
; therefore one has
$(M-1)(N-1)=1$
; therefore one has
![]() $(M,N)=(2,2)$
.
$(M,N)=(2,2)$
.
If
![]() $g=0$
and
$g=0$
and
![]() $L=2$
, then one has
$L=2$
, then one has
![]() $MN-N-M-MN/e=-1$
. If
$MN-N-M-MN/e=-1$
. If
![]() $4$
divides neither M nor N, one has
$4$
divides neither M nor N, one has
![]() $e=2\mathrm {lcm}(M,N)$
. Then
$e=2\mathrm {lcm}(M,N)$
. Then
![]() $\mathrm {gcd}(M,N)$
divides
$\mathrm {gcd}(M,N)$
divides
![]() $2$
, and is equal to
$2$
, and is equal to
![]() $2$
. Then one has
$2$
. Then one has
![]() $MN-N-M-1=-2$
, as above. As
$MN-N-M-1=-2$
, as above. As
![]() $L=2$
, the cases
$L=2$
, the cases
![]() $M=1$
and
$M=1$
and
![]() $N=1$
are excluded; thus, one has
$N=1$
are excluded; thus, one has
![]() $(M,N)=(2,2)$
.
$(M,N)=(2,2)$
.
Proposition 3.4 The genus g of the curve
![]() $X_{M, N,L}$
is equal to
$X_{M, N,L}$
is equal to
![]() $1$
for the following values of
$1$
for the following values of
![]() $(N,M,L)$
, and only for those values (up to permutation of N and M):
$(N,M,L)$
, and only for those values (up to permutation of N and M):
![]() $(3,2,1)$
,
$(3,2,1)$
,
![]() $(4,2,1)$
,
$(4,2,1)$
,
![]() $(4,2,2)$
,
$(4,2,2)$
,
![]() $(3,3,1)$
,
$(3,3,1)$
,
![]() $(3,3,3)$
.
$(3,3,3)$
.
The Jacobian varieties of those curves are elliptic curves endowed with automorphisms of order
![]() $3$
,
$3$
,
![]() $4$
,
$4$
,
![]() $4$
,
$4$
,
![]() $3$
, and
$3$
, and
![]() $3$
, respectively. Consequently, the j-invariants of those curves are
$3$
, respectively. Consequently, the j-invariants of those curves are
![]() $0$
,
$0$
,
![]() $1728$
,
$1728$
,
![]() $1728$
,
$1728$
,
![]() $0,$
and
$0,$
and
![]() $0$
, respectively.
$0$
, respectively.
Proof Consider again the formula:
![]() $2-2g=-L(MN-N-M-MN/e)$
. Thus,
$2-2g=-L(MN-N-M-MN/e)$
. Thus,
![]() ${g=1}$
amounts to
${g=1}$
amounts to
![]() $MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=0$
. One has
$MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=0$
. One has
![]() $MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=(N-2) (M-1)-2+M(1-N/e)$
. We can suppose that
$MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=(N-2) (M-1)-2+M(1-N/e)$
. We can suppose that
![]() $N>1$
and
$N>1$
and
![]() $M>1$
(otherwise
$M>1$
(otherwise
![]() $g=0$
).
$g=0$
).
If
![]() $N=2$
, one gets
$N=2$
, one gets
![]() $M(1-2/e)=2$
. If
$M(1-2/e)=2$
. If
![]() $L=1$
, then
$L=1$
, then
![]() $e=\mathrm {lcm}(M,2)$
. Thus,
$e=\mathrm {lcm}(M,2)$
. Thus,
![]() $M-1=2$
or
$M-1=2$
or
![]() $M-2=2$
. One has
$M-2=2$
. One has
![]() $(N,M,L)=(2,3,1)$
or
$(N,M,L)=(2,3,1)$
or
![]() $(N,M,L)=(2,4,1)$
.
$(N,M,L)=(2,4,1)$
.
If
![]() $N=2$
and
$N=2$
and
![]() $L=2$
, then
$L=2$
, then
![]() $e=2M$
or
$e=2M$
or
![]() $e=M$
. If
$e=M$
. If
![]() $e=M$
, then
$e=M$
, then
![]() $M-2=2$
. If
$M-2=2$
. If
![]() $e=2M$
, then
$e=2M$
, then
![]() $M-1=2$
(absurd since
$M-1=2$
(absurd since
![]() $L|M$
). One has
$L|M$
). One has
![]() $(N,M,L)=(2,4,2)$
or
$(N,M,L)=(2,4,2)$
or
![]() $(N,M,L)=(2,4,1)$
.
$(N,M,L)=(2,4,1)$
.
If
![]() $N=3$
, then one has
$N=3$
, then one has
![]() $M-3+M(1-3/e)=0$
and
$M-3+M(1-3/e)=0$
and
![]() $e=\mathrm {lcm}(M,3)$
. One can suppose that
$e=\mathrm {lcm}(M,3)$
. One can suppose that
![]() $M>2$
. Thus, one has
$M>2$
. Thus, one has
![]() $M=3$
and
$M=3$
and
![]() $L=1$
or
$L=1$
or
![]() $L=3$
. One has
$L=3$
. One has
![]() $(N,M,L)=(3,3,1)$
or
$(N,M,L)=(3,3,1)$
or
![]() $(N,M,L)=(3,3,3)$
.
$(N,M,L)=(3,3,3)$
.
The case where
![]() $M=2$
or
$M=2$
or
![]() $M=3$
are treated similarly. If
$M=3$
are treated similarly. If
![]() $N>3$
and
$N>3$
and
![]() $M>3$
, one has
$M>3$
, one has
![]() $(N-2)(M-1)-2+M(1-N/e)>0$
, which precludes
$(N-2)(M-1)-2+M(1-N/e)>0$
, which precludes
![]() $g=1$
.
$g=1$
.
The automorphisms come from the action of the image of A in
![]() $H_{N,M,L}$
which stabilizes a cusp and therefore is an automorphism of an elliptic curve.
$H_{N,M,L}$
which stabilizes a cusp and therefore is an automorphism of an elliptic curve.
We can derive some information on the Manin–Drinfeld principle in the genus
![]() $1$
cases.
$1$
cases.
Proposition 3.5 Divisors of the form
![]() $(CP)-(P)$
, where P is any point (in particular, a cusp) of
$(CP)-(P)$
, where P is any point (in particular, a cusp) of
![]() $X_{3,3,3}$
(resp.
$X_{3,3,3}$
(resp.
![]() $X_{4,2,2}$
) and C acts via the map
$X_{4,2,2}$
) and C acts via the map
![]() $\bar \Gamma (2)\rightarrow H_{N,M,L}$
, are of order dividing
$\bar \Gamma (2)\rightarrow H_{N,M,L}$
, are of order dividing
![]() $3$
(resp.
$3$
(resp.
![]() $2$
).
$2$
).
Proof The canonical morphism
![]() $X_{3,3,3}\rightarrow X_{3,3,1}$
is of degree
$X_{3,3,3}\rightarrow X_{3,3,1}$
is of degree
![]() $3$
. It gives rise to an isogeny of degree
$3$
. It gives rise to an isogeny of degree
![]() $3$
on the Jacobians by Albanese functionality. Thus, the kernel of this isogeny is of order
$3$
on the Jacobians by Albanese functionality. Thus, the kernel of this isogeny is of order
![]() $3$
. Moreover, any divisor of the form
$3$
. Moreover, any divisor of the form
![]() $(CP)-(P)$
is in the kernel of the isogeny.
$(CP)-(P)$
is in the kernel of the isogeny.
3.4 The curve
 $X'(2)$
$X'(2)$
Recall that the group
![]() $\bar \Gamma '(2)$
is the subgroup of index
$\bar \Gamma '(2)$
is the subgroup of index
![]() $3$
of
$3$
of
![]() $\bar \Gamma (2)$
that is the inverse image of the
$\bar \Gamma (2)$
that is the inverse image of the
![]() $2$
-Sylow subgroup of
$2$
-Sylow subgroup of
![]() $\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Denote by
$\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Denote by
![]() $X'(2)=X_{\Gamma '(2)}$
the corresponding modular curve.
$X'(2)=X_{\Gamma '(2)}$
the corresponding modular curve.
Proposition 3.6 The curve
![]() $X'(2)$
is of genus
$X'(2)$
is of genus
![]() $1$
and its j-invariant is
$1$
and its j-invariant is
![]() $0$
.
$0$
.
Proof Consider the morphism of degree
![]() $d=3$
:
$d=3$
:
![]() $X'(2)\rightarrow X(2)$
. Since none of the matrices A (generator of the stabilizer of the cusp
$X'(2)\rightarrow X(2)$
. Since none of the matrices A (generator of the stabilizer of the cusp
![]() $\infty $
), B (generator of the stabilizer of the cusp
$\infty $
), B (generator of the stabilizer of the cusp
![]() $0$
), and
$0$
), and
![]() $AB^{-1}$
(generator of the stabilizer of the cusp
$AB^{-1}$
(generator of the stabilizer of the cusp
![]() $1$
) are not in
$1$
) are not in
![]() $\bar \Gamma (2)$
, the morphism is totally ramified at each of the three cusps of
$\bar \Gamma (2)$
, the morphism is totally ramified at each of the three cusps of
![]() $X(2)$
, and ramified only over those points. The Riemann–Hurwitz formula expresses the genus g of
$X(2)$
, and ramified only over those points. The Riemann–Hurwitz formula expresses the genus g of
![]() $X'(2)$
as
$X'(2)$
as
![]() $(2g-2)=-2d+\sum _P(e_P-1)=6-6=0$
(where P runs through points of ramification and
$(2g-2)=-2d+\sum _P(e_P-1)=6-6=0$
(where P runs through points of ramification and
![]() $e_P$
designates the ramification index at that point), hence
$e_P$
designates the ramification index at that point), hence
![]() $g=1$
.
$g=1$
.
The curve
![]() $X'(2)$
has an automorphism (the class of A in
$X'(2)$
has an automorphism (the class of A in
![]() $\bar \Gamma (2)/\bar \Gamma '(2)$
) of order
$\bar \Gamma (2)/\bar \Gamma '(2)$
) of order
![]() $3$
which leaves fixed the cusp
$3$
which leaves fixed the cusp
![]() $\infty $
. Since it is of genus
$\infty $
. Since it is of genus
![]() $1$
, it is an elliptic curve of with an automorphism of order
$1$
, it is an elliptic curve of with an automorphism of order
![]() $3$
. It has necessarily j-invariant
$3$
. It has necessarily j-invariant
![]() $0$
.
$0$
.
Remark 3.7 Since
![]() $\Gamma _{3,3,3}=\Phi ^{\prime }_3$
is a subgroup of index
$\Gamma _{3,3,3}=\Phi ^{\prime }_3$
is a subgroup of index
![]() $3$
of
$3$
of
![]() $\Gamma '(2)$
. One has a morphism
$\Gamma '(2)$
. One has a morphism
![]() $X_{3,3,3}\rightarrow X'(2)$
of degree
$X_{3,3,3}\rightarrow X'(2)$
of degree
![]() $3$
. Both curves involved are of genus
$3$
. Both curves involved are of genus
![]() $1$
, so we have an isogeny of degree
$1$
, so we have an isogeny of degree
![]() $3$
. Note that
$3$
. Note that
![]() $\bar \Gamma '(2)$
is a congruence subgroup of level
$\bar \Gamma '(2)$
is a congruence subgroup of level
![]() $12$
and a subgroup of index
$12$
and a subgroup of index
![]() $3$
of the derived subgroup
$3$
of the derived subgroup
![]() $\tilde \Gamma $
of
$\tilde \Gamma $
of
![]() $\mathrm {PSL}_2({\mathbb {Z}})$
. The latter subgroup defined a modular curve
$\mathrm {PSL}_2({\mathbb {Z}})$
. The latter subgroup defined a modular curve
![]() $X_{\tilde \Gamma }$
of genus
$X_{\tilde \Gamma }$
of genus
![]() $1$
, which happens to have j-invariant
$1$
, which happens to have j-invariant
![]() $0$
. Thus, we get an isogeny
$0$
. Thus, we get an isogeny
![]() $X'(2)\rightarrow X_{\tilde \Gamma }$
of degree
$X'(2)\rightarrow X_{\tilde \Gamma }$
of degree
![]() $3$
.
$3$
.
We now prove Theorem 1.3.
Proof The correspondence is obtained by composing pushing to
![]() $X_{\Gamma. \Phi ^{\prime }_d}$
and pulling back to
$X_{\Gamma. \Phi ^{\prime }_d}$
and pulling back to
![]() $X_\Gamma $
. By Proposition 2.12, one has
$X_\Gamma $
. By Proposition 2.12, one has
![]() $\Gamma. \Phi ^{\prime }_d=\bar \Gamma (2)$
except if
$\Gamma. \Phi ^{\prime }_d=\bar \Gamma (2)$
except if
![]() $3$
divides N and
$3$
divides N and
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $\bar \Gamma '(2)$
. In the latter case,
$\bar \Gamma '(2)$
. In the latter case,
![]() $\theta _{N,\Gamma }$
factorizes through the Jacobian of
$\theta _{N,\Gamma }$
factorizes through the Jacobian of
![]() $X(2)$
, which is
$X(2)$
, which is
![]() $0$
. Otherwise, namely if
$0$
. Otherwise, namely if
![]() $3$
divides N and
$3$
divides N and
![]() $\Gamma $
is contained in
$\Gamma $
is contained in
![]() $\bar \Gamma '(2)$
,
$\bar \Gamma '(2)$
,
![]() $\theta _{N,\Gamma }$
factorizes through the surjective map
$\theta _{N,\Gamma }$
factorizes through the surjective map
![]() $J^{\prime }_N\rightarrow J'(2)$
. Since
$J^{\prime }_N\rightarrow J'(2)$
. Since
![]() $J'(2)$
is the Jacobian of a curve of genus
$J'(2)$
is the Jacobian of a curve of genus
![]() $1$
, and j-invariant
$1$
, and j-invariant
![]() $0$
, it is an elliptic curve of j-invariant
$0$
, it is an elliptic curve of j-invariant
![]() $0$
. Moreover, the map
$0$
. Moreover, the map
![]() $J'(2)\rightarrow J_\Gamma $
has finite kernel. The result follows.
$J'(2)\rightarrow J_\Gamma $
has finite kernel. The result follows.
It is well-known that the modular curve
![]() $X_0(27)$
has j-invariant
$X_0(27)$
has j-invariant
![]() $0$
, and that the Fermat curve is a model for
$0$
, and that the Fermat curve is a model for
![]() $X_0(27)$
. We might expect a connection between
$X_0(27)$
. We might expect a connection between
![]() $X_0(27)$
and
$X_0(27)$
and
![]() $X^{\prime }_3$
. Let
$X^{\prime }_3$
. Let
![]() $\Gamma =\bar \Gamma (2)\cap \Gamma _0(27)$
. It is a congruence subgroup. But it is not contained in
$\Gamma =\bar \Gamma (2)\cap \Gamma _0(27)$
. It is a congruence subgroup. But it is not contained in
![]() $\Gamma '(2)$
. Thus, if we apply Theorem 1.3 to the group
$\Gamma '(2)$
. Thus, if we apply Theorem 1.3 to the group
![]() $\Gamma $
, we obtain, counterintuitively, the
$\Gamma $
, we obtain, counterintuitively, the
![]() $0$
-morphism
$0$
-morphism
![]() $J^{\prime }_3\rightarrow J_{\Gamma }$
. A fortiori, if we push forward
$J^{\prime }_3\rightarrow J_{\Gamma }$
. A fortiori, if we push forward
![]() $J_\Gamma \rightarrow J_0(27)$
we obtain
$J_\Gamma \rightarrow J_0(27)$
we obtain
![]() $0$
.
$0$
.
3.5 Mixed homology groups
In [Reference Ejder5], the homology group of
![]() $X_N$
relative to the whole set of cusps is thoroughly studied, by the method of Manin [Reference Manin9]. We found fruitful in [Reference Banerjee and Merel2] to consider the following slightly different point of view: for
$X_N$
relative to the whole set of cusps is thoroughly studied, by the method of Manin [Reference Manin9]. We found fruitful in [Reference Banerjee and Merel2] to consider the following slightly different point of view: for
![]() $\Gamma $
a subgroup of finite index of
$\Gamma $
a subgroup of finite index of
![]() $\bar \Gamma (2)$
, the corresponding modular curve
$\bar \Gamma (2)$
, the corresponding modular curve
![]() $X_\Gamma $
covers
$X_\Gamma $
covers
![]() $X(2)$
, which admits three cusps:
$X(2)$
, which admits three cusps:
![]() $\Gamma (2)0$
,
$\Gamma (2)0$
,
![]() $\Gamma (2)1$
, and
$\Gamma (2)1$
, and
![]() $\Gamma (2)\infty $
. Let
$\Gamma (2)\infty $
. Let
![]() $\partial _\Gamma ^+$
(resp.
$\partial _\Gamma ^+$
(resp.
![]() $\partial _\Gamma ^-$
) be the set of cusps above
$\partial _\Gamma ^-$
) be the set of cusps above
![]() $\Gamma (2)0\cup \Gamma (2)\infty $
(resp.
$\Gamma (2)0\cup \Gamma (2)\infty $
(resp.
![]() $\Gamma (2)1$
)). It is thus possible to consider the mixed homology group
$\Gamma (2)1$
)). It is thus possible to consider the mixed homology group
![]() $\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
(and its dual
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
(and its dual
![]() $\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{+}, \partial _{\Gamma }^{-}; {{\mathbb {Z}}})$
). One gets a group isomorphism
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{+}, \partial _{\Gamma }^{-}; {{\mathbb {Z}}})$
). One gets a group isomorphism
which, for
![]() $g\in \bar \Gamma (2)$
, associates to
$g\in \bar \Gamma (2)$
, associates to
![]() $\Gamma g$
the class
$\Gamma g$
the class
![]() $\xi _\Gamma (g)$
in
$\xi _\Gamma (g)$
in
![]() $\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
of a path from
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
of a path from
![]() $g0$
to
$g0$
to
![]() $g\infty $
in the upper half-plane.
$g\infty $
in the upper half-plane.
Consider now the case where
![]() $\Gamma =\Phi ^{\prime }_N$
. To simplify notations, set
$\Gamma =\Phi ^{\prime }_N$
. To simplify notations, set
![]() $\partial ^{+}=\partial ^+$
and
$\partial ^{+}=\partial ^+$
and
![]() $\partial ^{-}=\partial ^-$
. Recall that we have a group isomorphism
$\partial ^{-}=\partial ^-$
. Recall that we have a group isomorphism
![]() $\Phi _N'\backslash \Gamma (2)\rightarrow H_{N,N,N'}$
which, for
$\Phi _N'\backslash \Gamma (2)\rightarrow H_{N,N,N'}$
which, for
![]() $(a,b,c)\in ({{\mathbb {Z}}})^{3}$
, to
$(a,b,c)\in ({{\mathbb {Z}}})^{3}$
, to
![]() $\Phi ^{\prime }_NA^aC^cB^b$
associates
$\Phi ^{\prime }_NA^aC^cB^b$
associates
![]() $x^az^cy^b$
. We get thus a group isomorphism
$x^az^cy^b$
. We get thus a group isomorphism
For
![]() $(a,b,c)\in ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, set
$(a,b,c)\in ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, set
![]() $i(a,b,c)=\xi ^{+}_{\Phi ^{\prime }_N}(\Phi ^{\prime }_{N}A^{a}C^{c}B^{b})$
.
$i(a,b,c)=\xi ^{+}_{\Phi ^{\prime }_N}(\Phi ^{\prime }_{N}A^{a}C^{c}B^{b})$
.
Thus,
![]() $H_{N,N,N'}$
acts on the curve
$H_{N,N,N'}$
acts on the curve
![]() $X^{\prime }_{N}$
, and transitively on the sets of cusps of
$X^{\prime }_{N}$
, and transitively on the sets of cusps of
![]() $X^{\prime }_{N}$
above
$X^{\prime }_{N}$
above
![]() $0$
,
$0$
,
![]() $1$
, and
$1$
, and
![]() $\infty $
, respectively. Thus, the stabilizer of a cusp is cyclic of order N.
$\infty $
, respectively. Thus, the stabilizer of a cusp is cyclic of order N.
The long exact sequence of relative homology yields:
where
![]() $\delta _N$
is the boundary map. Similarly we have a dual exact sequence:
$\delta _N$
is the boundary map. Similarly we have a dual exact sequence:
where
![]() $\delta _N^*$
is the dual boundary map. It induces
$\delta _N^*$
is the dual boundary map. It induces
Hence,
![]() $\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
can be described as a subquotient of the group
$\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
can be described as a subquotient of the group
![]() $\mathrm H_1(X^{\prime }_N-\partial ^-,\partial ^+;{\mathbb {Z}})$
. We will make this explicit by spelling out the maps
$\mathrm H_1(X^{\prime }_N-\partial ^-,\partial ^+;{\mathbb {Z}})$
. We will make this explicit by spelling out the maps
![]() $\delta _N$
and
$\delta _N$
and
![]() $\delta _N^*$
.
$\delta _N^*$
.
The sets of cusps of
![]() $X^{\prime }_N$
lying above
$X^{\prime }_N$
lying above
![]() $\infty $
,
$\infty $
,
![]() $0$
and
$0$
and
![]() $1$
are, respectively,
$1$
are, respectively,
![]() $\Phi _N'\backslash \Gamma (2)/A^{{\mathbb {Z}}}$
,
$\Phi _N'\backslash \Gamma (2)/A^{{\mathbb {Z}}}$
,
![]() $\Phi _N' \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
and
$\Phi _N' \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
and
![]() $\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}} $
. All three sets can be understood as follows.
$\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}} $
. All three sets can be understood as follows.
Proposition 3.8 We have three bijective maps as follows:
given by
![]() $x^{a} z^cy^{b}\mapsto (b,c+ab)$
,
$x^{a} z^cy^{b}\mapsto (b,c+ab)$
,
given by
![]() $x^a z^c y^{b}\mapsto (a,c)$
, and
$x^a z^c y^{b}\mapsto (a,c)$
, and
given by
![]() $x^a z^c y^{b}\mapsto (a+b,c-b(b+1)/2)$
.
$x^a z^c y^{b}\mapsto (a+b,c-b(b+1)/2)$
.
Proof The first two identifications are straightforward. We establish the third one. Let k be an integer. One finds by induction on k,
![]() $x^a z^c y^{b}(xy^{-1})^{k}=x^{a+k}z^{c-kb+k(k-1)/2}y^{b-k}$
. Since
$x^a z^c y^{b}(xy^{-1})^{k}=x^{a+k}z^{c-kb+k(k-1)/2}y^{b-k}$
. Since
![]() $(a+k)+(b-k)=a+b$
and
$(a+k)+(b-k)=a+b$
and
the map passes indeed to the quotient
![]() $\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
. It is surjective (take
$\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
. It is surjective (take
![]() $b=0$
). Since there are
$b=0$
). Since there are
![]() $NN'$
cusps above
$NN'$
cusps above
![]() $1$
, it is bijective.
$1$
, it is bijective.
Denote by
![]() $j_\infty (b,c)$
the cusp
$j_\infty (b,c)$
the cusp
![]() $\Phi _N'A^{a}C^{c-ab}B^bA^{N{\mathbb {Z}}}$
, for any
$\Phi _N'A^{a}C^{c-ab}B^bA^{N{\mathbb {Z}}}$
, for any
![]() $a\in {\mathbb {Z}}$
, by
$a\in {\mathbb {Z}}$
, by
![]() $j_0(a,c)$
the cusp
$j_0(a,c)$
the cusp
![]() $\Phi _N'A^{a}C^{c}B^{b}B^{N{\mathbb {Z}}}$
, for any
$\Phi _N'A^{a}C^{c}B^{b}B^{N{\mathbb {Z}}}$
, for any
![]() $b\in {\mathbb {Z}}$
, and
$b\in {\mathbb {Z}}$
, and
![]() $j_{1}(d,c)$
the cusp
$j_{1}(d,c)$
the cusp
![]() $\Phi _N'A^{a}C^{c-b(b+1)/2}B^{b}(AB^{-1})^{N{\mathbb {Z}}}$
, for any a,
$\Phi _N'A^{a}C^{c-b(b+1)/2}B^{b}(AB^{-1})^{N{\mathbb {Z}}}$
, for any a,
![]() $b\in {\mathbb {Z}}$
such that
$b\in {\mathbb {Z}}$
such that
![]() $a+b=d$
. With these conventions we can express
$a+b=d$
. With these conventions we can express
![]() $\delta _{N}$
.
$\delta _{N}$
.
Proposition 3.9 Let a, b,
![]() $c\in {\mathbb {Z}}$
. One has
$c\in {\mathbb {Z}}$
. One has
![]() $\delta _N(i(a,b,c))=j_\infty (b,c-ab)-j_0(a,c)$
.
$\delta _N(i(a,b,c))=j_\infty (b,c-ab)-j_0(a,c)$
.
Proof The boundary of the modular symbol
![]() $\{A^{a}C^{c}B^{b}0, A^{a}C^{c}B^{b}\infty \}$
is
$\{A^{a}C^{c}B^{b}0, A^{a}C^{c}B^{b}\infty \}$
is
which translates immediately into the claimed formula.
We use [Reference Banerjee and Merel2, Proposition 5] to determine
![]() $\delta _N^*$
.
$\delta _N^*$
.
Proposition 3.10 One has, for
![]() $d\in {\mathbb {Z}}/N{\mathbb {Z}}$
and
$d\in {\mathbb {Z}}/N{\mathbb {Z}}$
and
![]() $c\in {\mathbb {Z}}/N'{\mathbb {Z}}$
,
$c\in {\mathbb {Z}}/N'{\mathbb {Z}}$
,
 $$\begin{align*}\delta_N^*(j_{1}(d,c))=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}i(a,b+1,c-b(b+1)/2)-i(a,b,c-b(b+1)/2). \end{align*}$$
$$\begin{align*}\delta_N^*(j_{1}(d,c))=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}i(a,b+1,c-b(b+1)/2)-i(a,b,c-b(b+1)/2). \end{align*}$$
Proof We just need to translate the third statement [Reference Banerjee and Merel2, Proposition 5]. With the notations of that proposition, we have
![]() $w_{1}=N$
. It remains to use the third bijection of Proposition 3.8 and the definition of i.
$w_{1}=N$
. It remains to use the third bijection of Proposition 3.8 and the definition of i.
Let
![]() $S_{N}$
be the subgroup of
$S_{N}$
be the subgroup of
![]() ${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
formed by the elements of the form
${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
formed by the elements of the form
![]() $\sum \limits _{a,b,c}\lambda _{a,b,c}[a,b,c]$
, satisfying, for every
$\sum \limits _{a,b,c}\lambda _{a,b,c}[a,b,c]$
, satisfying, for every
![]() $(a,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
$(a,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
![]() $\sum \limits _{b\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c}=0$
and, for every
$\sum \limits _{b\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c}=0$
and, for every
![]() $(b,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
$(b,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
![]() $\sum \limits _{a\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c+ab}=0$
. By Proposition 3.9, its image by i has boundary
$\sum \limits _{a\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c+ab}=0$
. By Proposition 3.9, its image by i has boundary
![]() $0$
.
$0$
.
Let
![]() $R_{N}$
be the subgroup of
$R_{N}$
be the subgroup of
![]() ${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
spanned by elements of the form
${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
spanned by elements of the form
 $$\begin{align*}e_{c,d}=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}[a,b+1,c-b(b+1)/2)]-[a,b,c-b(b+1)/2], \end{align*}$$
$$\begin{align*}e_{c,d}=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}[a,b+1,c-b(b+1)/2)]-[a,b,c-b(b+1)/2], \end{align*}$$
for
![]() $(d,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
. By Proposition 3.10, it is a subgroup of
$(d,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
. By Proposition 3.10, it is a subgroup of
![]() $S_{N}$
. Thus, we get a presentation by generators and relations of the homology of
$S_{N}$
. Thus, we get a presentation by generators and relations of the homology of
![]() $X^{\prime }_{N}$
.
$X^{\prime }_{N}$
.
Corollary 3.11 The map i produces an exact sequence
Remark 3.12 By exchanging the roles of
![]() $\partial ^{+}$
and
$\partial ^{+}$
and
![]() $\partial ^{-}$
, it is possible to give a dual presentation of
$\partial ^{-}$
, it is possible to give a dual presentation of
![]() $\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
. We leave this to the reader.
$\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
. We leave this to the reader.
4 The Heisenberg covering and its models
In this section, we assume N to be odd. Therefore
![]() $N'=N$
.
$N'=N$
.
4.1 Modular functions
Let
![]() $z\in \mathbb {H}$
. For
$z\in \mathbb {H}$
. For
![]() $q_2=\exp {(\pi i z)}$
, consider the classical
$q_2=\exp {(\pi i z)}$
, consider the classical
![]() $\lambda $
-function [Reference Murty and Ramakrishnan13]:
$\lambda $
-function [Reference Murty and Ramakrishnan13]:
 $$\begin{align*}\lambda(z)=16 q_2 \prod_{n \geq 1} \left( \frac{1+q_2^{2n}}{1+q_2^{2n-1}}\right)^8, 1-\lambda(z)=\prod_{n \geq 1} \left( \frac{1-q_2^{2n-1}}{1+q_2^{2n-1}}\right)^8. \end{align*}$$
$$\begin{align*}\lambda(z)=16 q_2 \prod_{n \geq 1} \left( \frac{1+q_2^{2n}}{1+q_2^{2n-1}}\right)^8, 1-\lambda(z)=\prod_{n \geq 1} \left( \frac{1-q_2^{2n-1}}{1+q_2^{2n-1}}\right)^8. \end{align*}$$
From the above expression, it is clear that
![]() $\lambda (1)=1$
and
$\lambda (1)=1$
and
![]() $(1-\lambda (1))=0$
. The Nth roots
$(1-\lambda (1))=0$
. The Nth roots
define modular units for
![]() $\Phi _{N}$
. We recover thus the familiar model of the Fermat curve.
$\Phi _{N}$
. We recover thus the familiar model of the Fermat curve.
Since the
![]() $\lambda $
function identifies
$\lambda $
function identifies
![]() ${\mathbb {P}}^1-\{0,1,\infty \}$
to
${\mathbb {P}}^1-\{0,1,\infty \}$
to
![]() $Y(2)$
, a covering of
$Y(2)$
, a covering of
![]() ${\mathbb {P}}^1-\{0,1,\infty \}$
can be understood as a covering of
${\mathbb {P}}^1-\{0,1,\infty \}$
can be understood as a covering of
![]() $Y(2)$
, i.e., a modular curve.
$Y(2)$
, i.e., a modular curve.
4.2 Reminder on Fermat curves
The Nth Fermat curve
![]() $F_{N}$
is given by the projective model:
$F_{N}$
is given by the projective model:
Fermat curves and their points at infinity (cusps) are studied extensively by Rohrlich [Reference Rohrlich16, Reference Rohrlich17], Vélu [Reference Vélu18], and Posingies [Reference Posingies15]. In particular, these authors consider the map
given by
![]() $(X:Y:Z) \rightarrow (X^N:Z^N)$
. The map
$(X:Y:Z) \rightarrow (X^N:Z^N)$
. The map
![]() $\beta _N$
is of degree
$\beta _N$
is of degree
![]() $N^{2}$
. It is ramified only above the points
$N^{2}$
. It is ramified only above the points
![]() $0,1,\infty $
. The corresponding ramification points are given by
$0,1,\infty $
. The corresponding ramification points are given by
![]() $a_j=(0:\zeta ^j:1)$
,
$a_j=(0:\zeta ^j:1)$
,
![]() $b_j=(\zeta ^j:0:1)$
,
$b_j=(\zeta ^j:0:1)$
,
![]() $c_j=(\epsilon \zeta ^j:1:0)$
, for
$c_j=(\epsilon \zeta ^j:1:0)$
, for
![]() $j\in {\mathbb {Z}}/N{\mathbb {Z}}$
.
$j\in {\mathbb {Z}}/N{\mathbb {Z}}$
.
Recall that
![]() $\zeta $
is a primitive Nth root of unity and
$\zeta $
is a primitive Nth root of unity and
![]() $\epsilon $
is a square root of
$\epsilon $
is a square root of
![]() $\zeta $
. Each of the above points has ramification index N over
$\zeta $
. Each of the above points has ramification index N over
![]() ${\mathbb {P}}^1$
. For all
${\mathbb {P}}^1$
. For all
![]() $j\in {\mathbb {Z}}/N{\mathbb {Z}}$
, the cusps
$j\in {\mathbb {Z}}/N{\mathbb {Z}}$
, the cusps
![]() $a_j$
,
$a_j$
,
![]() $b_j$
,
$b_j$
,
![]() $c_j$
are all defined over the cyclotomic field
$c_j$
are all defined over the cyclotomic field
![]() $\mathbb {Q}(\mu _N)$
. Among them, only
$\mathbb {Q}(\mu _N)$
. Among them, only
![]() $a_0$
,
$a_0$
,
![]() $b_0$
, and
$b_0$
, and
![]() $c_0$
are defined over
$c_0$
are defined over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
4.3 The cuspidal subgroup of the Fermat curve
The divisors of following modular functions are given by:
Rohrlich [Reference Rohrlich17] has determined the structure of the cuspidal group of the Jacobian of
![]() $F_{N}$
(see also Vélu’s alternative proof and description [Reference Vélu18]). Since every cuspidal divisor on
$F_{N}$
(see also Vélu’s alternative proof and description [Reference Vélu18]). Since every cuspidal divisor on
![]() $F_{N}$
is annihilated by N in the Jacobian, the cuspidal group is a quotient of
$F_{N}$
is annihilated by N in the Jacobian, the cuspidal group is a quotient of
![]() ${\mathbb {Z}}/N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. The additional relations are given as follows. Recall that N is odd.
${\mathbb {Z}}/N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. The additional relations are given as follows. Recall that N is odd.
Theorem 4.1 (Rohrlich [Reference Rohrlich17])
The group
![]() $\mathcal {P}$
of principal divisors is spanned by the following set:
$\mathcal {P}$
of principal divisors is spanned by the following set:
 $$ \begin{align*}\bigg\{\sum_{i=0}^{N-1}[a_{i}]-[P],\sum_{i=0}^{N-1}[b_{i}]-[P],\sum_{i=0}^{N-1}[c_{i}]-[P], \end{align*} $$
$$ \begin{align*}\bigg\{\sum_{i=0}^{N-1}[a_{i}]-[P],\sum_{i=0}^{N-1}[b_{i}]-[P],\sum_{i=0}^{N-1}[c_{i}]-[P], \end{align*} $$
 $$ \begin{align*}\sum_{i=0}^{N-1}i([a_{i}]-[b_{i}]),\sum_{i=0}^{N-1}i([a_{i}]-[c_{i}]),\sum_{i=0}^{N-1}i^{2}([a_{i}]+[b_{i}]+[c_{i}]-3[P])\bigg\}, \end{align*} $$
$$ \begin{align*}\sum_{i=0}^{N-1}i([a_{i}]-[b_{i}]),\sum_{i=0}^{N-1}i([a_{i}]-[c_{i}]),\sum_{i=0}^{N-1}i^{2}([a_{i}]+[b_{i}]+[c_{i}]-3[P])\bigg\}, \end{align*} $$
where P is any cusp of
![]() $F_{N}$
. Thus, the cuspidal subgroup of the Jacobian of
$F_{N}$
. Thus, the cuspidal subgroup of the Jacobian of
![]() $F_N$
is a free
$F_N$
is a free
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
-module of rank
${\mathbb {Z}}/N{\mathbb {Z}}$
-module of rank
![]() $3N-7$
.
$3N-7$
.
We set
(resp.
![]() $D_{B}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[b_{i}]$
, resp.
$D_{B}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[b_{i}]$
, resp.
![]() $D_{C}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[c_{i}]$
) and
$D_{C}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[c_{i}]$
) and
Corollary 4.2 The class of
![]() $D_A$
is of order N in the cuspidal subgroup of the Jacobian of
$D_A$
is of order N in the cuspidal subgroup of the Jacobian of
![]() $F_N$
. Moreover, it is congruent to
$F_N$
. Moreover, it is congruent to
![]() $D_B$
and
$D_B$
and
![]() $D_C$
modulo
$D_C$
modulo
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Proof Indeed, the divisor of
![]() $f_A$
is
$f_A$
is
![]() $ND_A$
. By Rohrlich’s theorem,
$ND_A$
. By Rohrlich’s theorem,
![]() $D_A$
is of order N. The congruence of
$D_A$
is of order N. The congruence of
![]() $D_A$
,
$D_A$
,
![]() $D_B$
, and
$D_B$
, and
![]() $D_C$
modulo
$D_C$
modulo
![]() $\mathcal {P}$
follows from Rohrlich’s relations.
$\mathcal {P}$
follows from Rohrlich’s relations.
4.4 The covering as a function field extension
By Rohrlich’s theorem, the order of
![]() $D_{A}$
in the cuspidal group is N, therefore an Nth root of
$D_{A}$
in the cuspidal group is N, therefore an Nth root of
![]() $f_{A}$
defines a cyclic covering
$f_{A}$
defines a cyclic covering
![]() $G\rightarrow F_{N}$
(a provisional notation, since G will be shown to be equal to
$G\rightarrow F_{N}$
(a provisional notation, since G will be shown to be equal to
![]() $F_N'$
) of degree N. Such a morphism is indeed unramified, since the divisor of
$F_N'$
) of degree N. Such a morphism is indeed unramified, since the divisor of
![]() $f_{A}$
belongs to
$f_{A}$
belongs to
![]() $N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. Since
$N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. Since
![]() $D_{A}-D_{B}$
is a principal divisor, exchanging the roles of X and Y would give the same covering. A similar reasoning with respect to
$D_{A}-D_{B}$
is a principal divisor, exchanging the roles of X and Y would give the same covering. A similar reasoning with respect to
![]() $D_{C}$
holds. The cyclic covering
$D_{C}$
holds. The cyclic covering
![]() $G\rightarrow F_{N}$
translates into a covering of Riemann surfaces
$G\rightarrow F_{N}$
translates into a covering of Riemann surfaces
![]() $W\rightarrow X_{N}$
.
$W\rightarrow X_{N}$
.
Consider now the third term
![]() $[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
in the lower central series of
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
in the lower central series of
![]() $\Gamma (2)$
. It is not a subgroup of finite index of
$\Gamma (2)$
. It is not a subgroup of finite index of
![]() $\Gamma (2)$
, but one can still consider the Riemann surface
$\Gamma (2)$
, but one can still consider the Riemann surface
![]() $X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
Proposition 4.3 The covering
![]() $W\rightarrow X_{N}$
factorizes through
$W\rightarrow X_{N}$
factorizes through
![]() $X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
Proof Let
![]() $U\in \Gamma (2)$
and
$U\in \Gamma (2)$
and
![]() $V\in [\Gamma (2),\Gamma (2)]]$
. Let g be an Nth root of
$V\in [\Gamma (2),\Gamma (2)]]$
. Let g be an Nth root of
![]() $f_{A}$
. One has to prove that g is invariant under
$f_{A}$
. One has to prove that g is invariant under
![]() $[U,V]$
, that is,
$[U,V]$
, that is,
![]() $g_{|UV}=g_{|VU}$
. Note first that
$g_{|UV}=g_{|VU}$
. Note first that
![]() $y_{|U}=\zeta ^{r}y$
, with
$y_{|U}=\zeta ^{r}y$
, with
![]() $r\in {{\mathbb {Z}}}$
. One has
$r\in {{\mathbb {Z}}}$
. One has
Write
![]() $\{i+r\}=\{i\}+r+t$
, with
$\{i+r\}=\{i\}+r+t$
, with
![]() $t\in N{\mathbb {Z}}$
. Thus, we get
$t\in N{\mathbb {Z}}$
. Thus, we get
The last factor is obviously an Nth power. By the description of Rohrlich of the cuspidal subgroup of
![]() $F_{N}$
, the factor
$F_{N}$
, the factor
![]() $\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
is an Nth power in the function field of
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
is an Nth power in the function field of
![]() $F_{N}$
. So there exists a function h on
$F_{N}$
. So there exists a function h on
![]() $F_{N}$
, and an integer s such that
$F_{N}$
, and an integer s such that
![]() $g_{|U}=g\zeta ^{s}h$
. Note that
$g_{|U}=g\zeta ^{s}h$
. Note that
![]() $h_{|V}=h$
and
$h_{|V}=h$
and
![]() $g_{|V}=\zeta ^{q}g$
, with
$g_{|V}=\zeta ^{q}g$
, with
![]() $q\in {\mathbb {Z}}$
. Therefore, one has
$q\in {\mathbb {Z}}$
. Therefore, one has
Proposition 4.4 Any covering of degree N of the Fermat modular curve
![]() $X_{N}$
that factors through
$X_{N}$
that factors through
![]() $X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, factors through the Heisenberg covering.
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, factors through the Heisenberg covering.
Proof Such a covering corresponds to a cyclic quotient of order N of
![]() $\Phi _{N}$
. Denote by
$\Phi _{N}$
. Denote by
![]() $\Gamma $
the corresponding cocyclic subgroup of
$\Gamma $
the corresponding cocyclic subgroup of
![]() $\Phi _{N}$
. Since the covering is unramified at the cusps,
$\Phi _{N}$
. Since the covering is unramified at the cusps,
![]() $\Gamma $
contains the matrices
$\Gamma $
contains the matrices
![]() $A^{N}$
and
$A^{N}$
and
![]() $B^{N}$
. Recall that
$B^{N}$
. Recall that
![]() $\Phi _{N}$
is generated by
$\Phi _{N}$
is generated by
![]() $A^{N}$
,
$A^{N}$
,
![]() $B^{N}$
and the commutator subgroup of
$B^{N}$
and the commutator subgroup of
![]() $\Gamma (2)$
. Since the covering factors through
$\Gamma (2)$
. Since the covering factors through
![]() $X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, the group
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, the group
![]() $\Gamma $
contains
$\Gamma $
contains
![]() $[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
. In particular,
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
. In particular,
![]() $\Gamma $
contains
$\Gamma $
contains
![]() $[A,C]$
and
$[A,C]$
and
![]() $[B,C]$
. Thus, the image of C in
$[B,C]$
. Thus, the image of C in
![]() $\Phi _{N}/\Gamma $
is of order N. Consequently,
$\Phi _{N}/\Gamma $
is of order N. Consequently,
![]() $\Gamma $
is the group generated by
$\Gamma $
is the group generated by
![]() $[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
,
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
,
![]() $A^{N}$
,
$A^{N}$
,
![]() $B^{N}$
,
$B^{N}$
,
![]() $C^{N}$
.
$C^{N}$
.
Corollary 4.5 Let
![]() $\zeta $
be a primitive Nth root of unity in
$\zeta $
be a primitive Nth root of unity in
![]() $\mathbb {Q}(\mu _N)$
. The function
$\mathbb {Q}(\mu _N)$
. The function
admits an Nth root in the function field of
![]() $F^{\prime }_N$
.
$F^{\prime }_N$
.
Proof Indeed, the covering of
![]() $F_{N}$
defined by an Nth root of
$F_{N}$
defined by an Nth root of
![]() $f_{A}'$
is cyclic of order N and factorizes through
$f_{A}'$
is cyclic of order N and factorizes through
![]() $X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
. Consequently, it is
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
. Consequently, it is
![]() $F^{\prime }_{N}$
.
$F^{\prime }_{N}$
.
Let K be the field of fractions of the curve given in the introduction over the complex numbers. In inhomogeneous form, it is generated by the variable X, Y,
![]() $T_{\zeta }$
for every primitive Nth root of unity
$T_{\zeta }$
for every primitive Nth root of unity
![]() $\zeta $
, with the relations
$\zeta $
, with the relations
and, for every primitive Nth root of unity
![]() $\zeta $
(in
$\zeta $
(in
![]() $\mathbf {Q}(\mu _{N})$
)
$\mathbf {Q}(\mu _{N})$
)
 $$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
Corollary 4.6 The function field of
![]() $F^{\prime }_{N}$
over
$F^{\prime }_{N}$
over
![]() $\mathbb {C}$
is isomorphic to K.
$\mathbb {C}$
is isomorphic to K.
Proof Indeed, the function field of
![]() $F^{\prime }_{N}$
is the subfield of K generated by an Nth root of
$F^{\prime }_{N}$
is the subfield of K generated by an Nth root of
![]() $f_{A}$
over the function field of
$f_{A}$
over the function field of
![]() $F_{N}$
. Let
$F_{N}$
. Let
![]() $\zeta '$
be a primitive Nth root of unity. By the preceding corollary,
$\zeta '$
be a primitive Nth root of unity. By the preceding corollary,
![]() $T_{\zeta '}$
belongs to K. Thus, all of K is contained in the function field of
$T_{\zeta '}$
belongs to K. Thus, all of K is contained in the function field of
![]() $F^{\prime }_{N}$
.
$F^{\prime }_{N}$
.
Thus, we have shown that the curve
![]() $F^{\prime }_N$
extends the Riemann surface
$F^{\prime }_N$
extends the Riemann surface
![]() $X^{\prime }_N$
.
$X^{\prime }_N$
.
Corollary 4.7 The Riemann surfaces
![]() $X^{\prime }_N$
and
$X^{\prime }_N$
and
![]() $F^{\prime }_N({\mathbb {C}})$
are isomorphic.
$F^{\prime }_N({\mathbb {C}})$
are isomorphic.
4.5 The Heisenberg covering
Denote by G the Galois group of the field extension
![]() $K|\mathbb {Q}(X^N)$
. It sits in an exact sequence
$K|\mathbb {Q}(X^N)$
. It sits in an exact sequence
by the transitive action of G on Nth roots of unity, and the fact that the Heisenberg covering is defined over
![]() $\mathbb {Q}(\zeta )$
. Recall that for
$\mathbb {Q}(\zeta )$
. Recall that for
![]() $i\in ({\mathbb {Z}}/N{\mathbb {Z}})$
,
$i\in ({\mathbb {Z}}/N{\mathbb {Z}})$
,
![]() $\{i\}$
denotes the representative of i in
$\{i\}$
denotes the representative of i in
![]() $\{-(N-1)/2,\dots , (N-1)/2\}$
.
$\{-(N-1)/2,\dots , (N-1)/2\}$
.
Proposition 4.8 For
![]() $\sigma \in G$
, there exists u, v,
$\sigma \in G$
, there exists u, v,
![]() $s\in ({\mathbb {Z}}/N{\mathbb {Z}})$
and
$s\in ({\mathbb {Z}}/N{\mathbb {Z}})$
and
![]() $r\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
such that
$r\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
such that
![]() $\sigma (X)=\zeta ^uX$
,
$\sigma (X)=\zeta ^uX$
,
![]() $\sigma (Y)=\zeta ^v(Y)$
,
$\sigma (Y)=\zeta ^v(Y)$
,
![]() $\sigma (\zeta )=\zeta ^r$
. For
$\sigma (\zeta )=\zeta ^r$
. For
![]() $\rho $
a representative of r in
$\rho $
a representative of r in
![]() ${\mathbb {Z}}$
,
${\mathbb {Z}}$
,
Furthermore,
![]() $(u,v,s,r)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{3}\times ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
characterizes
$(u,v,s,r)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{3}\times ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
characterizes
![]() $\sigma $
.
$\sigma $
.
Proof The first three identities are evident. A simple calculation establishes the last one. Indeed,
By factoring
![]() $T^N$
and
$T^N$
and
![]() $\prod _i \zeta ^{v\{i\}}$
, and replacing the variable i by
$\prod _i \zeta ^{v\{i\}}$
, and replacing the variable i by
![]() $j=\rho i-v$
, one gets
$j=\rho i-v$
, one gets
We use
![]() $\prod _i \zeta ^{v\{i\}}=1$
and we get
$\prod _i \zeta ^{v\{i\}}=1$
and we get
Using the identity
![]() $X^N=(1-Y^N)=\prod _{j\in ({\mathbb {Z}}/N{\mathbb {Z}})}(-Y+\zeta ^{j})$
, we get
$X^N=(1-Y^N)=\prod _{j\in ({\mathbb {Z}}/N{\mathbb {Z}})}(-Y+\zeta ^{j})$
, we get
The desired formula follows by taking Nth roots.
With the notations of the proposition, we note
![]() $\sigma =\sigma _{u,v,r,s}$
. Murty and Rama krishnan note that Deligne showed that
$\sigma =\sigma _{u,v,r,s}$
. Murty and Rama krishnan note that Deligne showed that
![]() $F^{\prime }_N$
can be defined over
$F^{\prime }_N$
can be defined over
![]() $\mathbb {Q}$
, without giving a reference. We spell out this assertion.
$\mathbb {Q}$
, without giving a reference. We spell out this assertion.
Proposition 4.9 The curve
![]() $F^{\prime }_N$
can be defined over
$F^{\prime }_N$
can be defined over
![]() $\mathbb {Q}$
. More precisely, the surjective map
$\mathbb {Q}$
. More precisely, the surjective map
![]() $G\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
admits the map
$G\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
admits the map
![]() $r\mapsto \sigma _{0,0,r,0}$
as a section. Denote by S the corresponding subgroup of G. It acts trivially on Nth roots of unity. Consequently, the field of invariants by S in K is the function field of a curve over
$r\mapsto \sigma _{0,0,r,0}$
as a section. Denote by S the corresponding subgroup of G. It acts trivially on Nth roots of unity. Consequently, the field of invariants by S in K is the function field of a curve over
![]() $\mathbb {Q}$
, and defines
$\mathbb {Q}$
, and defines
![]() $F^{\prime }_N$
over
$F^{\prime }_N$
over
![]() $\mathbb {Q}$
. The Heisenberg covering
$\mathbb {Q}$
. The Heisenberg covering
![]() $F^{\prime }_N\rightarrow F_N$
extends also over
$F^{\prime }_N\rightarrow F_N$
extends also over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof Group theoretic arguments about the structure of G as an extension imply easily the existence of the section. We will show that our explicit map is indeed a section. Let r,
![]() $r'\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
and
$r'\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
and
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
be representatives of r and
$\rho '$
be representatives of r and
![]() $r'$
, respectively, in
$r'$
, respectively, in
![]() ${\mathbb {Z}}$
. We need to check that
${\mathbb {Z}}$
. We need to check that
![]() $\sigma _{0,0,r',0}\sigma _{0,0,r,0}=\sigma _{0,0,rr',0}$
, which need to be verified only by application on T, or equivalently on
$\sigma _{0,0,r',0}\sigma _{0,0,r,0}=\sigma _{0,0,rr',0}$
, which need to be verified only by application on T, or equivalently on
![]() $T^{\rho \rho '}$
, and on
$T^{\rho \rho '}$
, and on
![]() $\zeta $
. This is trivial for
$\zeta $
. This is trivial for
![]() $\zeta $
. Here is the computation on
$\zeta $
. Here is the computation on
![]() $T^{\rho \rho '}$
. We first simplify the formula of the previous proposition
$T^{\rho \rho '}$
. We first simplify the formula of the previous proposition
Thus, one has
 $$ \begin{align*}&\sigma_{0,0,r',0}\sigma_{0,0,r,0}(T^{\rho\rho'})\\&\quad=T\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{(\rho'\{j/\rho'\}-\{j\})/N}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{\rho'j})^{(\rho\{j/\rho\}-\{j\})\rho'/N}). \end{align*} $$
$$ \begin{align*}&\sigma_{0,0,r',0}\sigma_{0,0,r,0}(T^{\rho\rho'})\\&\quad=T\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{(\rho'\{j/\rho'\}-\{j\})/N}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{\rho'j})^{(\rho\{j/\rho\}-\{j\})\rho'/N}). \end{align*} $$
A change of variable in the second product of the right-hand side gives
4.6 Automorphisms
The group
![]() $({\mathbb {Z}}/N{\mathbb {Z}})^{2}\simeq \Gamma (2)/\Phi _{N}$
acts on
$({\mathbb {Z}}/N{\mathbb {Z}})^{2}\simeq \Gamma (2)/\Phi _{N}$
acts on
![]() $F_{N}$
:
$F_{N}$
:
![]() $(i,j)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{2}$
acts by the rule
$(i,j)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{2}$
acts by the rule
![]() $(x,y)\mapsto (\zeta ^{i}x,\zeta ^{j}y)$
. Such an action is defined on
$(x,y)\mapsto (\zeta ^{i}x,\zeta ^{j}y)$
. Such an action is defined on
![]() $\mathbb {Q}(\mu _{N})$
. It lifts to an action of
$\mathbb {Q}(\mu _{N})$
. It lifts to an action of
![]() $H_{{\mathbb {Z}}/N{\mathbb {Z}}}\simeq \Gamma (2)/\Phi _{N}'$
on
$H_{{\mathbb {Z}}/N{\mathbb {Z}}}\simeq \Gamma (2)/\Phi _{N}'$
on
![]() $F_{N}'$
.
$F_{N}'$
.
Lemma 4.10 The action of
![]() $H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
on
$H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
on
![]() $F_{N}'$
is defined over
$F_{N}'$
is defined over
![]() $\mathbb {Q}(\mu _{N})$
.
$\mathbb {Q}(\mu _{N})$
.
Proof For
![]() $U\in H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, one needs to check that the action of U on a
$U\in H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, one needs to check that the action of U on a
![]() $\mathbb {Q}(\zeta )$
-rational function is still
$\mathbb {Q}(\zeta )$
-rational function is still
![]() $\mathbb {Q}(\zeta )$
-rational. It suffices to verify this for g, an Nth root of
$\mathbb {Q}(\zeta )$
-rational. It suffices to verify this for g, an Nth root of
![]() $f_{A}$
. We repeat a previous calculation and get
$f_{A}$
. We repeat a previous calculation and get
with
![]() $t\in N{\mathbb {Z}}$
. Both factors
$t\in N{\mathbb {Z}}$
. Both factors
![]() $\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
and
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
and
![]() $\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{t}$
are Nth power, (of, say,
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{t}$
are Nth power, (of, say,
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{2}$
) in the function field of
$g_{2}$
) in the function field of
![]() $F_{N}$
over
$F_{N}$
over
![]() $\mathbb {Q}(\zeta )$
. We thus find that
$\mathbb {Q}(\zeta )$
. We thus find that
![]() $g_{|U}$
is equal to
$g_{|U}$
is equal to
![]() $\zeta ^{p}gg_{1}g_{2}$
, which belongs to the function field of
$\zeta ^{p}gg_{1}g_{2}$
, which belongs to the function field of
![]() $X_{N}$
over
$X_{N}$
over
![]() $\mathbb {Q}(\zeta )$
.
$\mathbb {Q}(\zeta )$
.
Remark 4.11 We do not give an explicit algebraic model of the curve
![]() $X^{\prime \prime }_{N}$
. But it can be obtained by taking
$X^{\prime \prime }_{N}$
. But it can be obtained by taking
![]() $N"$
th roots of the functions whose divisors are
$N"$
th roots of the functions whose divisors are
![]() $\sum _{i=0}^{N-1}i^{2}([a_{i}]-[P])\}$
,
$\sum _{i=0}^{N-1}i^{2}([a_{i}]-[P])\}$
,
![]() $\sum _{i=0}^{N-1}i^{2}([b_{i}]-[P])\}$
and
$\sum _{i=0}^{N-1}i^{2}([b_{i}]-[P])\}$
and
![]() $\sum _{i=0}^{N-1}i^{2}([c_{i}]-[P])\}$
.
$\sum _{i=0}^{N-1}i^{2}([c_{i}]-[P])\}$
.
4.7 Regular integral models of Heisenberg curves
We relate the Heisenberg covering to the model given in the introduction. Note that the inhomogeneous version of the projective model is given by
and, for every primitive Nth root of unity
![]() $\zeta $
(in a fixed cyclotomic extension of
$\zeta $
(in a fixed cyclotomic extension of
![]() $\mathbf {Q}$
)
$\mathbf {Q}$
)
 $$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
We now prove Theorem 1.1 (in the spirit of, e.g., [Reference Curilla3, Proposition 1.1.13]).
Proof We have indeed a scheme of relative dimension
![]() $1$
over
$1$
over
![]() $\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
. We just have to establish the smoothness. We use the Jacobian criterion (e.g., [Reference Liu8, p. 130, Theorem 2.19]).
$\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
. We just have to establish the smoothness. We use the Jacobian criterion (e.g., [Reference Liu8, p. 130, Theorem 2.19]).
Since the Heisenberg covering is obtained by taking the Nth root of a function which does not vanish outside the zero locus of
![]() $XY$
, all points away from
$XY$
, all points away from
![]() $X=0$
and
$X=0$
and
![]() $Y=0$
are regular in all characteristics prime to N. It remains to establish the regularity of a point
$Y=0$
are regular in all characteristics prime to N. It remains to establish the regularity of a point
![]() $P_{\zeta }$
of the form
$P_{\zeta }$
of the form
![]() $(X,Y)=(0,\zeta )$
or
$(X,Y)=(0,\zeta )$
or
![]() $(X,Y)=(\zeta ,0)$
with
$(X,Y)=(\zeta ,0)$
with
![]() $\zeta $
a primitive Nth root of unity. Suppose
$\zeta $
a primitive Nth root of unity. Suppose
![]() $(X,Y)=(0,\zeta )$
. For points of this form, one has
$(X,Y)=(0,\zeta )$
. For points of this form, one has
![]() $T_{\zeta }=0$
. We set
$T_{\zeta }=0$
. We set
 $$\begin{align*}F_{\zeta}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}-\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j} \end{align*}$$
$$\begin{align*}F_{\zeta}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}-\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j} \end{align*}$$
and compute the partial derivative at
![]() $P_{\zeta }$
. One obtains
$P_{\zeta }$
. One obtains
 $$\begin{align*}\frac{\partial F_{\zeta}}{\partial Y}(P_{\zeta})=- \prod_{j=2}^{(N-1)/2}(\zeta-\zeta^{j})^{j}, \end{align*}$$
$$\begin{align*}\frac{\partial F_{\zeta}}{\partial Y}(P_{\zeta})=- \prod_{j=2}^{(N-1)/2}(\zeta-\zeta^{j})^{j}, \end{align*}$$
which is a cyclotomic unit that belongs to
![]() $\mathbf {Z}[\mu _{N},1/N]^{\times }$
. Thus, the Jacobian matrix is nonzero over any fiber in characteristic prime to N. This is sufficient to establish the regularity of
$\mathbf {Z}[\mu _{N},1/N]^{\times }$
. Thus, the Jacobian matrix is nonzero over any fiber in characteristic prime to N. This is sufficient to establish the regularity of
![]() $P_{\zeta }$
over
$P_{\zeta }$
over
![]() $\mathrm {Spec}(\mathbf {Z}[\mu _{N},1/N])$
since the structural morphism is of relative dimension
$\mathrm {Spec}(\mathbf {Z}[\mu _{N},1/N])$
since the structural morphism is of relative dimension
![]() $1$
. This reasoning applies to the zero locus of Y, by exchanging the roles of X and Y.
$1$
. This reasoning applies to the zero locus of Y, by exchanging the roles of X and Y.
4.8 Cusps
The term cusp refers to the cusps of the modular curve
![]() $X_\Gamma $
attached to a subgroup
$X_\Gamma $
attached to a subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Gamma (2)$
. These points are not intrinsic to the corresponding algebraic curves. In the cases of interest to us, we have a morphism
$\Gamma (2)$
. These points are not intrinsic to the corresponding algebraic curves. In the cases of interest to us, we have a morphism
![]() $X_N\rightarrow X(2)$
, given by the function
$X_N\rightarrow X(2)$
, given by the function
![]() $x^N$
. Thus, the cusps of
$x^N$
. Thus, the cusps of
![]() $F_N$
are the
$F_N$
are the
![]() $3N$
points above the points
$3N$
points above the points
![]() $0$
,
$0$
,
![]() $1$
, and
$1$
, and
![]() $\infty $
described above.
$\infty $
described above.
Since the morphism
![]() $F^{\prime }_N\rightarrow F_N$
is unramified, the modular curve
$F^{\prime }_N\rightarrow F_N$
is unramified, the modular curve
![]() $F^{\prime }_N$
possesses
$F^{\prime }_N$
possesses
![]() $3N^2$
cusps.
$3N^2$
cusps.
Proposition 4.12 If N is prime to
![]() $3$
, the cusps of
$3$
, the cusps of
![]() $F^{\prime }_N$
are defined over
$F^{\prime }_N$
are defined over
![]() $\mathbb {Q}(\zeta )$
. If
$\mathbb {Q}(\zeta )$
. If
![]() $3$
divides N, the cusps of
$3$
divides N, the cusps of
![]() $F^{\prime }_N$
are defined over the cyclotomic field generated by the
$F^{\prime }_N$
are defined over the cyclotomic field generated by the
![]() $3N$
th roots of unity.
$3N$
th roots of unity.
Proof Let a be a cusp of
![]() $F^{\prime }_{N}$
above
$F^{\prime }_{N}$
above
![]() $a_{0}$
. It is defined over the field generated by
$a_{0}$
. It is defined over the field generated by
![]() $g(a)$
and
$g(a)$
and
![]() $\mathbb {Q}(\zeta )$
, where g is an Nth root of
$\mathbb {Q}(\zeta )$
, where g is an Nth root of
![]() $f_{A}$
. One has
$f_{A}$
. One has
 $$ \begin{align*}f_{A}(a_{0})=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-1+\zeta^{i})^{\{i\}}=\prod_{i=1}^{(N-1)/2}\frac{(-1+\zeta^{i})^{i}}{(-1+\zeta^{-i})^{i}}=\prod_{i=1}^{(N-1)/2}(-\zeta^{i})^{i}. \end{align*} $$
$$ \begin{align*}f_{A}(a_{0})=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-1+\zeta^{i})^{\{i\}}=\prod_{i=1}^{(N-1)/2}\frac{(-1+\zeta^{i})^{i}}{(-1+\zeta^{-i})^{i}}=\prod_{i=1}^{(N-1)/2}(-\zeta^{i})^{i}. \end{align*} $$
Thus, we get
which is a sixth root of unity.
Suppose N is prime to
![]() $3$
. Then
$3$
. Then
![]() $g(a)$
is an Nth root of unity, up to sign. Since the group
$g(a)$
is an Nth root of unity, up to sign. Since the group
![]() $H_{N}$
acts transitively on the cups above
$H_{N}$
acts transitively on the cups above
![]() $\infty $
, and its action is
$\infty $
, and its action is
![]() $\mathbb {Q}(\zeta )$
-rational, we deduce that all the cusps above
$\mathbb {Q}(\zeta )$
-rational, we deduce that all the cusps above
![]() $\infty $
are defined over
$\infty $
are defined over
![]() $\mathbb {Q}(\zeta )$
. A similar reasoning apply to the cusps above
$\mathbb {Q}(\zeta )$
. A similar reasoning apply to the cusps above
![]() $0$
, and above
$0$
, and above
![]() $1$
.
$1$
.
A similar reasoning applies when
![]() $3$
divides N. Indeed,
$3$
divides N. Indeed,
![]() $g(a)$
is a
$g(a)$
is a
![]() $3N$
th root of unity, up to sign.
$3N$
th root of unity, up to sign.
The cusps of
![]() $F^{\prime }_N$
above the cusp
$F^{\prime }_N$
above the cusp
![]() $\infty $
(resp.
$\infty $
(resp.
![]() $0$
, resp.
$0$
, resp.
![]() $1$
) of
$1$
) of
![]() $X(2)$
coincide with the classes
$X(2)$
coincide with the classes
![]() $\Gamma \backslash \Gamma (2)\infty $
(resp.
$\Gamma \backslash \Gamma (2)\infty $
(resp.
![]() $\Gamma \backslash \Gamma (2)0$
, resp.
$\Gamma \backslash \Gamma (2)0$
, resp.
![]() $\Gamma \backslash \Gamma (2)1$
), which in turn can be identified with the double classes
$\Gamma \backslash \Gamma (2)1$
), which in turn can be identified with the double classes
![]() $\Gamma \backslash \Gamma (2)/A^{{\mathbb {Z}}}$
(resp.
$\Gamma \backslash \Gamma (2)/A^{{\mathbb {Z}}}$
(resp.
![]() $\Gamma \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
, resp.
$\Gamma \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
, resp.
![]() $\Gamma \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
).
$\Gamma \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
).
4.9 About the Manin–Drinfeld principle for
 $F^{\prime }_3$
$F^{\prime }_3$
Recall that
![]() $g_{3}=1$
and observe that
$g_{3}=1$
and observe that
![]() $F^{\prime }_{3}$
has 27 cusps. Fix one cusp
$F^{\prime }_{3}$
has 27 cusps. Fix one cusp
![]() $P_{0}$
of
$P_{0}$
of
![]() $F^{\prime }_{3}$
, which becomes thus an elliptic curve
$F^{\prime }_{3}$
, which becomes thus an elliptic curve
![]() $(F^{\prime }_{3}, P_{0})$
. Since a cyclic group of order
$(F^{\prime }_{3}, P_{0})$
. Since a cyclic group of order
![]() $3$
acts on
$3$
acts on
![]() $F^{\prime }_{3}$
and stabilizes
$F^{\prime }_{3}$
and stabilizes
![]() $P_{0}$
, the elliptic curve
$P_{0}$
, the elliptic curve
![]() $(F^{\prime }_{3}, P_{0})$
admits an automorphism of order
$(F^{\prime }_{3}, P_{0})$
admits an automorphism of order
![]() $3$
. Thus, the j-invariant of
$3$
. Thus, the j-invariant of
![]() $(F^{\prime }_{3}, P_{0})$
is
$(F^{\prime }_{3}, P_{0})$
is
![]() $0$
.
$0$
.
Proposition 4.13 Divisors supported on the cusps of
![]() $F^{\prime }_{3}$
above
$F^{\prime }_{3}$
above
![]() $\infty $
(resp.
$\infty $
(resp.
![]() $0$
, resp.
$0$
, resp.
![]() $1$
) are of order dividing
$1$
) are of order dividing
![]() $3$
in the Jacobian of
$3$
in the Jacobian of
![]() $F^{\prime }_{3}$
. Furthermore, cuspidal divisors of degree
$F^{\prime }_{3}$
. Furthermore, cuspidal divisors of degree
![]() $0$
are torsion in the Jacobian of
$0$
are torsion in the Jacobian of
![]() $F^{\prime }_3$
, and of order dividing
$F^{\prime }_3$
, and of order dividing
![]() $9$
.
$9$
.
Proof Let X be a compact connected Riemann surface of genus
![]() $1$
. Let J be the Jacobian of X. Recall the exact sequence
$1$
. Let J be the Jacobian of X. Recall the exact sequence
where
![]() $\mathrm {Aut}$
denotes the automorphisms over
$\mathrm {Aut}$
denotes the automorphisms over
![]() $\mathbf {C}$
. The first map associates to the class of a divisor D the translation by D in X.
$\mathbf {C}$
. The first map associates to the class of a divisor D the translation by D in X.
For
![]() $X=F^{\prime }_{3}$
, the group
$X=F^{\prime }_{3}$
, the group
![]() $\mathrm {Aut}(J)$
is cyclic of order
$\mathrm {Aut}(J)$
is cyclic of order
![]() $6$
. One gets a group homomorphism
$6$
. One gets a group homomorphism
![]() $H_{\mathbf {Z}/3\mathbf {Z}}\rightarrow \mathrm {Aut}(J)$
, whose kernel is of order
$H_{\mathbf {Z}/3\mathbf {Z}}\rightarrow \mathrm {Aut}(J)$
, whose kernel is of order
![]() $9$
, and therefore isomorphic to
$9$
, and therefore isomorphic to
![]() $(\mathbf { Z}/3\mathbf {Z})^{2}$
. Since this kernel identifies to a subgroup of the one dimensional complex torus
$(\mathbf { Z}/3\mathbf {Z})^{2}$
. Since this kernel identifies to a subgroup of the one dimensional complex torus
![]() $J(\mathbf {C})$
, the latter subgroup is
$J(\mathbf {C})$
, the latter subgroup is
![]() $J(\mathbf {C})[3]$
. We have proved that the orbit of any cups Q by
$J(\mathbf {C})[3]$
. We have proved that the orbit of any cups Q by
![]() $H_{\mathbf {Z}/3\mathbf {Z}}$
contains
$H_{\mathbf {Z}/3\mathbf {Z}}$
contains
![]() $Q+J(\mathbf {C})[3]$
. But these sets are both of cardinality
$Q+J(\mathbf {C})[3]$
. But these sets are both of cardinality
![]() $9$
, and are therefore equal. Since
$9$
, and are therefore equal. Since
![]() $H_{\mathbf {Z}/3\mathbf {Z}}$
acts transitively on the cusps above
$H_{\mathbf {Z}/3\mathbf {Z}}$
acts transitively on the cusps above
![]() $\infty $
(resp.
$\infty $
(resp.
![]() $0$
, resp.
$0$
, resp.
![]() $1$
), the first statement of the proposition is proved.
$1$
), the first statement of the proposition is proved.
About the second statement, it is sufficient to prove this for a divisor of the form
![]() $(\alpha )-(\beta ),$
where
$(\alpha )-(\beta ),$
where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are cusps of
$\beta $
are cusps of
![]() $F^{\prime }_3$
not above the same point of
$F^{\prime }_3$
not above the same point of
![]() $\{0,1,\infty \}$
. Without loss of generality, say they are above
$\{0,1,\infty \}$
. Without loss of generality, say they are above
![]() $0$
and
$0$
and
![]() $\infty $
, respectively. Let a and b be the cusps of
$\infty $
, respectively. Let a and b be the cusps of
![]() $F_3$
below
$F_3$
below
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively. We have
$\beta $
, respectively. We have
where
![]() $\alpha '$
(resp.
$\alpha '$
(resp.
![]() $\beta '$
) runs through the cusps of
$\beta '$
) runs through the cusps of
![]() $F^{\prime }_3$
above a (resp. b). By the first statement of the proposition and the torsion properties of the cuspidal subgroup of the
$F^{\prime }_3$
above a (resp. b). By the first statement of the proposition and the torsion properties of the cuspidal subgroup of the
![]() $F_3$
, each of the three terms of the right-hand side is of order dividing
$F_3$
, each of the three terms of the right-hand side is of order dividing
![]() $3$
.
$3$
.
Recall that the dessin for
![]() $X^{\prime }_{N}$
is a graph with the following additional structure: the vertices are bicolored (white and black) and the of set edges attached to any given vertex are endowed with a cyclic ordering (a transitive action of
$X^{\prime }_{N}$
is a graph with the following additional structure: the vertices are bicolored (white and black) and the of set edges attached to any given vertex are endowed with a cyclic ordering (a transitive action of
![]() ${\mathbb {Z}}$
). The vertices are the cusps of
${\mathbb {Z}}$
). The vertices are the cusps of
![]() $X^{\prime }_{N}$
above
$X^{\prime }_{N}$
above
![]() $0$
and
$0$
and
![]() $\infty $
. The edges form the coset
$\infty $
. The edges form the coset
![]() $\Phi ^{\prime }_{N}\backslash \Gamma (2)\simeq H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, which is in bijection with
$\Phi ^{\prime }_{N}\backslash \Gamma (2)\simeq H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, which is in bijection with
![]() $({\mathbb {Z}}/N{\mathbb {Z}})^{3}$
. the edge associated with
$({\mathbb {Z}}/N{\mathbb {Z}})^{3}$
. the edge associated with
![]() $\Phi ^{\prime }_{N}g$
has extremities
$\Phi ^{\prime }_{N}g$
has extremities
![]() $\Phi ^{\prime }_{N}g0$
and
$\Phi ^{\prime }_{N}g0$
and
![]() $\Phi ^{\prime }_{N}g\infty $
. The cyclic ordering of the edges attached to the vertices
$\Phi ^{\prime }_{N}g\infty $
. The cyclic ordering of the edges attached to the vertices
![]() $\Phi ^{\prime }_{N}g0$
(resp.
$\Phi ^{\prime }_{N}g0$
(resp.
![]() $\Phi ^{\prime }_{N}g\infty $
) is given by the action of B (resp.
$\Phi ^{\prime }_{N}g\infty $
) is given by the action of B (resp.
![]() $A^{-1}$
). To sum up, the dessin can be drawn on
$A^{-1}$
). To sum up, the dessin can be drawn on
![]() $X^{\prime }_{N}$
.
$X^{\prime }_{N}$
.
To be more concrete, each edge is in bijection with
![]() ${\mathbb {Z}}/N{\mathbb {Z}}\times {\mathbb {Z}}/N'{\mathbb {Z}}\times {\mathbb {Z}}/N{\mathbb {Z}}$
, via the map
${\mathbb {Z}}/N{\mathbb {Z}}\times {\mathbb {Z}}/N'{\mathbb {Z}}\times {\mathbb {Z}}/N{\mathbb {Z}}$
, via the map
![]() $\Phi ^{\prime }_{N}A^{a}C^{c}B^{b}\mapsto (a,c,b)$
. The edge thus labeled
$\Phi ^{\prime }_{N}A^{a}C^{c}B^{b}\mapsto (a,c,b)$
. The edge thus labeled
![]() $(a,c,b)$
is connected to the edge labeled
$(a,c,b)$
is connected to the edge labeled
![]() $(a,c,b+1)$
via a black vertex (cusp above
$(a,c,b+1)$
via a black vertex (cusp above
![]() $0$
) and the edge labeled
$0$
) and the edge labeled
![]() $(a,c,b)$
is connected to the edge labeled
$(a,c,b)$
is connected to the edge labeled
![]() $(a-1,c-ab,b)$
via a white vertex (cusp above
$(a-1,c-ab,b)$
via a white vertex (cusp above
![]() $\infty $
). The line segments represent the arcs on
$\infty $
). The line segments represent the arcs on
![]() $X^{\prime }_3$
above the geodesic arc from
$X^{\prime }_3$
above the geodesic arc from
![]() $0$
to
$0$
to
![]() $\infty $
in the upper half-plane.
$\infty $
in the upper half-plane.
We illustrate all this for
![]() $N=3$
. In that case, the genus of
$N=3$
. In that case, the genus of
![]() $X^{\prime }_{3}$
is equal to
$X^{\prime }_{3}$
is equal to
![]() $1$
. According to these rules, the drawing (dessin) for
$1$
. According to these rules, the drawing (dessin) for
![]() $X_3'$
is given as follows.
$X_3'$
is given as follows.

As the group
![]() $\Phi _{3}$
is not a congruence subgroup [Reference Phillips and Sarnak14],
$\Phi _{3}$
is not a congruence subgroup [Reference Phillips and Sarnak14],
![]() $\Phi ^{\prime }_{3}$
is a fortiori not a congruence subgroup. The latter fact can be derived alternately from Wolfart’s criterion and an examination of the dessin. Indeed, the width of the each cusps is equal to
$\Phi ^{\prime }_{3}$
is a fortiori not a congruence subgroup. The latter fact can be derived alternately from Wolfart’s criterion and an examination of the dessin. Indeed, the width of the each cusps is equal to
![]() $6$
and
$6$
and
![]() $[\Gamma (2):\Phi ^{\prime }_3]=27$
. Wolfart’s criterion, to check that
$[\Gamma (2):\Phi ^{\prime }_3]=27$
. Wolfart’s criterion, to check that
![]() $\Phi ^{\prime }_3$
is a congruence subgroup or not it is enough to check
$\Phi ^{\prime }_3$
is a congruence subgroup or not it is enough to check
![]() $\Gamma (6) \subset \Phi ^{\prime }_3 \subset \Gamma (2)$
. However,
$\Gamma (6) \subset \Phi ^{\prime }_3 \subset \Gamma (2)$
. However,
![]() $[\Gamma (2):\Gamma (6)]=144$
is not divisible by the index
$[\Gamma (2):\Gamma (6)]=144$
is not divisible by the index
![]() $27$
.
$27$
.
4.10 About the failure of the Manin–Drinfeld principle for
 $F^{\prime }_5$
$F^{\prime }_5$
Suppose
![]() $N=5$
. We show that the Manin–Drinfeld theorem fails for the Heisenberg covering
$N=5$
. We show that the Manin–Drinfeld theorem fails for the Heisenberg covering
![]() ${\mathcal {F}}^{\prime }_5$
of
${\mathcal {F}}^{\prime }_5$
of
![]() ${\mathcal {F}}_5$
. Consider the scheme
${\mathcal {F}}_5$
. Consider the scheme
![]() ${\mathcal {C}}_5$
over
${\mathcal {C}}_5$
over
![]() $\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _{5},1/5])$
given by the system of equations
$\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _{5},1/5])$
given by the system of equations
 $$ \begin{align*}T_\zeta^5=\frac{(-Y+\zeta)(-Y+\zeta^2)^2}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}, \end{align*} $$
$$ \begin{align*}T_\zeta^5=\frac{(-Y+\zeta)(-Y+\zeta^2)^2}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}, \end{align*} $$
where
![]() $\zeta $
runs through the primitive fifth roots of unity in
$\zeta $
runs through the primitive fifth roots of unity in
![]() $\mathbb {Q}(\mu _{5})$
. It is smooth, as can be shown by applying the Jacobian criterion. One has an obvious morphism of schemes
$\mathbb {Q}(\mu _{5})$
. It is smooth, as can be shown by applying the Jacobian criterion. One has an obvious morphism of schemes
![]() ${\mathcal {F}}^{\prime }_5\rightarrow {\mathcal {C}}_5$
.
${\mathcal {F}}^{\prime }_5\rightarrow {\mathcal {C}}_5$
.
Denote by
![]() $C_{5}$
the generic fiber of
$C_{5}$
the generic fiber of
![]() ${\mathcal {C}}_5$
. Over
${\mathcal {C}}_5$
. Over
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $C_5$
identifies to a modular curve as follows. Consider the morphism
$C_5$
identifies to a modular curve as follows. Consider the morphism
![]() $\bar \Gamma (2)\rightarrow H_{5,5,5}$
and the inverse image
$\bar \Gamma (2)\rightarrow H_{5,5,5}$
and the inverse image
![]() $\Gamma '$
of the subgroup of
$\Gamma '$
of the subgroup of
![]() $H_{5,5,5}$
generated by B. Then
$H_{5,5,5}$
generated by B. Then
![]() $\Gamma '$
defines a corresponding modular curve isomorphic to the Riemann surface
$\Gamma '$
defines a corresponding modular curve isomorphic to the Riemann surface
![]() $C_5(\mathbb {C})$
.
$C_5(\mathbb {C})$
.
The curve
![]() $C_{5}$
possesses
$C_{5}$
possesses
![]() $19$
cusps, given by the following planar coordinates
$19$
cusps, given by the following planar coordinates
![]() $(Y,T_{\zeta })$
:
$(Y,T_{\zeta })$
:
![]() $(0,\epsilon )$
,
$(0,\epsilon )$
,
![]() $(\infty , \epsilon )$
,
$(\infty , \epsilon )$
,
![]() $(1, -\delta )$
,
$(1, -\delta )$
,
![]() $(\zeta ,0)$
,
$(\zeta ,0)$
,
![]() $(\zeta ^2,0)$
,
$(\zeta ^2,0)$
,
![]() $(\zeta ^{-1},\infty )$
,
$(\zeta ^{-1},\infty )$
,
![]() $(\zeta ^{-2},\infty )$
, where
$(\zeta ^{-2},\infty )$
, where
![]() $\epsilon $
and
$\epsilon $
and
![]() $\delta $
run through the fifth roots of unity. Set
$\delta $
run through the fifth roots of unity. Set
![]() $T=T_{\zeta }$
. The function fields of
$T=T_{\zeta }$
. The function fields of
![]() $F^{\prime }_{5}$
and
$F^{\prime }_{5}$
and
![]() $C_{5}$
are
$C_{5}$
are
![]() $\mathbf {Q}(\zeta ,X,Y,T)$
and
$\mathbf {Q}(\zeta ,X,Y,T)$
and
![]() $\mathbf {Q}(\zeta ,Y,T)$
, respectively.
$\mathbf {Q}(\zeta ,Y,T)$
, respectively.
The obvious morphism
![]() $\pi $
:
$\pi $
:
![]() $F^{\prime }_5\rightarrow C_5$
sends the cusps of
$F^{\prime }_5\rightarrow C_5$
sends the cusps of
![]() $F^{\prime }_5$
to the cusps of
$F^{\prime }_5$
to the cusps of
![]() $C_5$
. We show that
$C_5$
. We show that
![]() $C_5$
does not satisfy the Manin–Drinfeld principle. Since
$C_5$
does not satisfy the Manin–Drinfeld principle. Since
![]() ${\mathcal {C}}_5$
is smooth, the Jacobian of
${\mathcal {C}}_5$
is smooth, the Jacobian of
![]() $C_5$
extends to an abelian scheme
$C_5$
extends to an abelian scheme
![]() ${\mathcal {J}}_5$
over
${\mathcal {J}}_5$
over
![]() $\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _5,1/5])$
.
$\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _5,1/5])$
.
Proposition 4.14 There exists a divisor of infinite order supported on the cusps of
![]() $C_{5}$
.
$C_{5}$
.
Proof We suppose that all cuspidal divisors are torsion in
![]() $C_{5}$
. Our proof is organized around the following calculation. One has
$C_{5}$
. Our proof is organized around the following calculation. One has
 $$ \begin{align} T^5+1=\frac{(1-Y)(2Y^2+(2-2(\zeta^2+\zeta^{-2})-\zeta-\zeta^{-1})Y+2)}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}. \end{align} $$
$$ \begin{align} T^5+1=\frac{(1-Y)(2Y^2+(2-2(\zeta^2+\zeta^{-2})-\zeta-\zeta^{-1})Y+2)}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}. \end{align} $$
Let
![]() $y_1$
and
$y_1$
and
![]() $y_2$
be the roots of the polynomial
$y_2$
be the roots of the polynomial
![]() $2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
. Let
$2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
. Let
![]() $\zeta _1$
be a fifth root of unity in
$\zeta _1$
be a fifth root of unity in
![]() $\mathbf {Z}[\mu _5]$
. Consider the function
$\mathbf {Z}[\mu _5]$
. Consider the function
![]() $T+\zeta _1$
, which divides
$T+\zeta _1$
, which divides
![]() $T^5+1$
. The divisor of the function
$T^5+1$
. The divisor of the function
![]() $T+\zeta _1$
is (in terms of planar coordinates for
$T+\zeta _1$
is (in terms of planar coordinates for
![]() $(Y,T)$
):
$(Y,T)$
):
![]() $(1,-\zeta _1)+(y_1,-\zeta _1)+(y_2,-\zeta _1)-D$
, where
$(1,-\zeta _1)+(y_1,-\zeta _1)+(y_2,-\zeta _1)-D$
, where
![]() $D=(\zeta ^{-1},\infty )+2(\zeta ^{-2},\infty )$
. Apparently fortuitously, this divisor is cuspidal in the fibers at
$D=(\zeta ^{-1},\infty )+2(\zeta ^{-2},\infty )$
. Apparently fortuitously, this divisor is cuspidal in the fibers at
![]() $11$
and at
$11$
and at
![]() $2$
of
$2$
of
![]() $C_{5}$
.
$C_{5}$
.
Lemma 4.15 Let
![]() $\zeta _1$
and
$\zeta _1$
and
![]() $\zeta _2$
be distinct primitive fifth roots of unity in
$\zeta _2$
be distinct primitive fifth roots of unity in
![]() ${\mathbb {Z}}[\mu _5]$
. The divisors
${\mathbb {Z}}[\mu _5]$
. The divisors
![]() $3(1,\zeta _1)-3(1,\zeta _2)$
and
$3(1,\zeta _1)-3(1,\zeta _2)$
and
![]() $3(1,\zeta _1)-D$
are principal in any fiber above
$3(1,\zeta _1)-D$
are principal in any fiber above
![]() $11$
of
$11$
of
![]() $C_5$
.
$C_5$
.
Proof In characteristic
![]() $11$
, the polynomial
$11$
, the polynomial
![]() $2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
has the providential property of having a double root equal to
$2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
has the providential property of having a double root equal to
![]() $1$
. Therefore, the divisor of the function
$1$
. Therefore, the divisor of the function
![]() $T+\zeta _1$
over
$T+\zeta _1$
over
![]() $\mathbb {F}_{11}$
is cuspidal and equal to
$\mathbb {F}_{11}$
is cuspidal and equal to
![]() $3(1,\zeta _1)-D$
. It follows that the function
$3(1,\zeta _1)-D$
. It follows that the function
![]() $(T+\zeta _1)/(T+\zeta _2)$
has divisor
$(T+\zeta _1)/(T+\zeta _2)$
has divisor
![]() $3(1,\zeta _1)-3(1,\zeta _2)$
.
$3(1,\zeta _1)-3(1,\zeta _2)$
.
We return to the proof of the proposition. By our Manin–Drinfeld assumption in
![]() $C_{5}$
, the divisor
$C_{5}$
, the divisor
![]() $3(1,\zeta _1)-D$
is torsion in the Jacobian of
$3(1,\zeta _1)-D$
is torsion in the Jacobian of
![]() $C_{5}$
. It extends to a torsion point of
$C_{5}$
. It extends to a torsion point of
![]() ${\mathcal {J}}_5$
, whose order is determined in any special fiber at a prime
${\mathcal {J}}_5$
, whose order is determined in any special fiber at a prime
![]() $\pi $
of residual characteristic p, provided
$\pi $
of residual characteristic p, provided
![]() $p-1>e$
, where e is the ramification index at
$p-1>e$
, where e is the ramification index at
![]() $\pi $
of the extension
$\pi $
of the extension
![]() ${\mathbb {Q}}(\mu _5)|{\mathbb {Q}}$
[Reference Mazur11]. This applies for any prime except perhaps
${\mathbb {Q}}(\mu _5)|{\mathbb {Q}}$
[Reference Mazur11]. This applies for any prime except perhaps
![]() $p=2$
and
$p=2$
and
![]() $p=5$
. The calculation for
$p=5$
. The calculation for
![]() $p=11$
ensures that the divisors
$p=11$
ensures that the divisors
![]() $3(1,\zeta _1)-3(1,\zeta _2)$
and
$3(1,\zeta _1)-3(1,\zeta _2)$
and
![]() $3(1,\zeta _1)-D$
are principal in
$3(1,\zeta _1)-D$
are principal in
![]() $C_{5}$
.
$C_{5}$
.
Therefore, those divisors are principal in any special fiber of
![]() ${\mathcal {C}}_5$
. Consider any fiber
${\mathcal {C}}_5$
. Consider any fiber
![]() $\bar {C}$
above
$\bar {C}$
above
![]() $2$
of
$2$
of
![]() $C_{5}$
. In that fiber, the function
$C_{5}$
. In that fiber, the function
![]() $T-\zeta =T+\zeta $
has divisor, in view of Equation (4.1),
$T-\zeta =T+\zeta $
has divisor, in view of Equation (4.1),
![]() $(0,\zeta )+(1,\zeta )+(\infty ,\zeta )-D_{\zeta }$
, which is principal. Thus, by taking
$(0,\zeta )+(1,\zeta )+(\infty ,\zeta )-D_{\zeta }$
, which is principal. Thus, by taking
![]() $\zeta _{1}=\zeta $
, the divisor
$\zeta _{1}=\zeta $
, the divisor
is principal in
![]() $\bar C$
. Thus, there exists f:
$\bar C$
. Thus, there exists f:
![]() ${\bar C}\rightarrow {\mathbb {P}}^{1}$
of degree
${\bar C}\rightarrow {\mathbb {P}}^{1}$
of degree
![]() $2$
. So
$2$
. So
![]() $\bar {C}$
is hyperelliptic. The principality of the divisor
$\bar {C}$
is hyperelliptic. The principality of the divisor
![]() $3(1,\zeta _1)-3(1,\zeta _2)$
ensures that there is a degree
$3(1,\zeta _1)-3(1,\zeta _2)$
ensures that there is a degree
![]() $3$
morphism
$3$
morphism
![]() $\bar C\rightarrow {\mathbb {P}}^{1}$
. By Castelnuovo–Severi-type inequalities, this imposes that the genus of
$\bar C\rightarrow {\mathbb {P}}^{1}$
. By Castelnuovo–Severi-type inequalities, this imposes that the genus of
![]() $\bar {C}$
is
$\bar {C}$
is
![]() $\le 2$
. But the genus of
$\le 2$
. But the genus of
![]() $\bar C$
equals the genus of
$\bar C$
equals the genus of
![]() $C_{5}$
; it is equal to
$C_{5}$
; it is equal to
![]() $6$
and we have reached a contradiction.
$6$
and we have reached a contradiction.