Research Article
On the Kneser-Hukuhara property for integral equations in locally convex spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-360
-
- Article
-
- You have access
- Export citation
The Nevanlinna-Pick theorem and a non-positive definite matrix
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-365
-
- Article
-
- You have access
- Export citation
Each weakly countably determined Asplund space admits a Fréchet differentiable norm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-374
-
- Article
-
- You have access
- Export citation
An extension of Müntz's theorems in multivariables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-387
-
- Article
-
- You have access
- Export citation
How complete are categories of algebras?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-409
-
- Article
-
- You have access
- Export citation
There are no chaotic mappings with residual scrambled sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 411-416
-
- Article
-
- You have access
- Export citation
Tensor products of function algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-423
-
- Article
-
- You have access
- Export citation
Estimates for solutions of elliptic equations in a limit case
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-434
-
- Article
-
- You have access
- Export citation
On the Stone-Čeck compactification of an orbit space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-439
-
- Article
-
- You have access
- Export citation
On maximum matchings in cubic graphs with a bounded number of bridge-covering paths
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-447
-
- Article
-
- You have access
- Export citation
On composite polynomials whose zeros are in a half-plane
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-460
-
- Article
-
- You have access
- Export citation
Two remarks on amalgams of locally finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-468
-
- Article
-
- You have access
- Export citation
Examples of expanding maps with some special properties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-474
-
- Article
-
- You have access
- Export citation
Modular fitting functors in finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-483
-
- Article
-
- You have access
- Export citation
A modified projection method for equations of the second kind
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 485-492
-
- Article
-
- You have access
- Export citation
Bounded and relatively bounded sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 493-498
-
- Article
-
- You have access
- Export citation
A note on additive mappings in noncommutative fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-502
-
- Article
-
- You have access
- Export citation
Going-down underrings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 503-513
-
- Article
-
- You have access
- Export citation
A remark on projective modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 515-520
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Extrema of Gaussian process by simulation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-522
-
- Article
-
- You have access
- Export citation



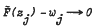 as
as 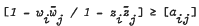 on
on 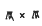 where
where  .
.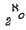 non amalgamation bases in the class of locally finite groups, and we present necessary and sufficient conditions for the embeddability of an amalgam into a locally finite group in the case that the common subgroup has finite index in both constituents.
non amalgamation bases in the class of locally finite groups, and we present necessary and sufficient conditions for the embeddability of an amalgam into a locally finite group in the case that the common subgroup has finite index in both constituents.