No CrossRef data available.
Published online by Cambridge University Press: 13 January 2023
Let 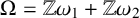 $\Omega =\mathbb {Z}\omega _1+\mathbb {Z}\omega _2$ be a lattice in
$\Omega =\mathbb {Z}\omega _1+\mathbb {Z}\omega _2$ be a lattice in  $\mathbb {C}$ with invariants
$\mathbb {C}$ with invariants 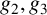 $g_2,g_3$ and
$g_2,g_3$ and 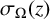 $\sigma _{\Omega }(z)$ the associated Weierstrass
$\sigma _{\Omega }(z)$ the associated Weierstrass 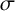 $\sigma $-function. Let
$\sigma $-function. Let 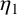 $\eta _1$ and
$\eta _1$ and 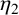 $\eta _2$ be the quasi-periods associated to
$\eta _2$ be the quasi-periods associated to 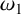 $\omega _1$ and
$\omega _1$ and 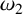 $\omega _2$, respectively. Assuming
$\omega _2$, respectively. Assuming 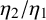 $\eta _2/\eta _1$ is a nonzero real number, we give an upper bound for the number of algebraic points on the graph of
$\eta _2/\eta _1$ is a nonzero real number, we give an upper bound for the number of algebraic points on the graph of 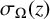 $\sigma _{\Omega }(z)$ of bounded degrees and bounded absolute Weil heights in some unbounded region of
$\sigma _{\Omega }(z)$ of bounded degrees and bounded absolute Weil heights in some unbounded region of  $\mathbb {C}$ in the following three cases: (i)
$\mathbb {C}$ in the following three cases: (i) 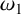 $\omega _1$ and
$\omega _1$ and 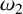 $\omega _2$ algebraic; (ii)
$\omega _2$ algebraic; (ii) 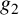 $g_2$ and
$g_2$ and 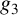 $g_3$ algebraic; (iii) the algebraic points are far from the lattice points.
$g_3$ algebraic; (iii) the algebraic points are far from the lattice points.
This research is partially supported by the MATRICS grant MTR/2021/000476 and the second author is thankful to the SERB, India.