Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-05-12T04:14:24.822Z Has data issue: false hasContentIssue false
  • English
  • Français

NUMBER THEORY PROBLEMS RELATED TO THE SPECTRUM OF CANTOR-TYPE MEASURES WITH CONSECUTIVE DIGITS

Part of: Normed linear spaces and Banach spaces; Banach lattices Nontrigonometric harmonic analysis Classical measure theory

Published online by Cambridge University Press:  10 June 2020

WEN-HUI AI Open the ORCID record for WEN-HUI AI [Opens in a new window]
WEN-HUI AI*
Affiliation:
College of Mathematics and Econometrics,Hunan University, Changsha, Hunan 410082, PR China email awhxyz123@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For integers 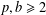$p,b\geq 2$, let 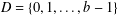$D=\{0,1,\ldots ,b-1\}$ be a set of consecutive digits. It is known that the Cantor measure 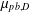$\unicode[STIX]{x1D707}_{pb,D}$ generated by the iterated function system 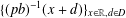$\{(pb)^{-1}(x+d)\}_{x\in \mathbb{R},d\in D}$ is a spectral measure with spectrum

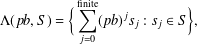$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(pb,S)=\bigg\{\mathop{\sum }_{j=0}^{\text{finite}}(pb)^{j}s_{j}:s_{j}\in S\bigg\},\end{eqnarray}$$
where $S=pD$. We give conditions on 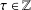$\unicode[STIX]{x1D70F}\in \mathbb{Z}$ under which the scaling set 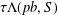$\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6EC}(pb,S)$ is also a spectrum of 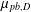$\unicode[STIX]{x1D707}_{pb,D}$. These investigations link number theory and spectral measures.

Keywords

Cantor-type setspectral measurescaling spectraextreme cycleHadamard triples

MSC classification

Primary: 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 113 - 123
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research is supported in part by the NNSF of China (No. 11831007) and by Hunan Provincial Innovation Foundation for Postgraduates (CX20190322).

References

An, L. X. and He, X. G., ‘A class of spectral Moran measures’, J. Funct. Anal. 266(1) (2014), 343–354.CrossRefGoogle Scholar
An, L. X., He, X. G. and Lau, K. S., ‘Spectrality of a class of infinite convolutions’, Adv. Math. 283 (2015), 362–376.CrossRefGoogle Scholar
Dai, X. R., ‘When does a Bernoulli convolution admit a spectrum?’, Adv. Math. 231 (2012), 1681–1693.10.1016/j.aim.2012.06.026CrossRefGoogle Scholar
Dai, X. R., He, X. G. and Lai, C. K., ‘Spectral property of Cantor measures with consecutive digits’, Adv. Math. 242 (2013), 187–208.10.1016/j.aim.2013.04.016CrossRefGoogle Scholar
Dai, X. R., He, X. G. and Lau, K. S., ‘On spectral N-Bernoulli measures’, Adv. Math. 259 (2014), 511–531.10.1016/j.aim.2014.03.026CrossRefGoogle Scholar
Dutkay, D. E., Han, D. G. and Sun, Q. Y., ‘On the spectra of a Cantor measure’, Adv. Math. 221(1) (2009), 251–276.CrossRefGoogle Scholar
Dutkay, D. E. and Haussermann, J., ‘Number theory problems from the harmonic analysis of a fractal’, J. Number Theory 159 (2016), 7–26.CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T., ‘Iterated function systems, Ruelle operators, and invariant projective measures’, Math. Comp. 75 (2006), 1931–1970 (electronic).CrossRefGoogle Scholar
Dutkay, D. E. and Jorgensen, P. E. T., ‘Fourier duality for fractal measures with affine scales’, Math. Comp. 81 (2012), 2253–2273.10.1090/S0025-5718-2012-02580-4CrossRefGoogle Scholar
Dutkay, D. E. and Kraus, I., ‘Number theoretic considerations related to the scaling of spectra of Cantor-type measures’, Anal. Math. 44(3) (2018), 335–367.CrossRefGoogle Scholar
Dutkay, D. E., Lai, C. K. and Wang, Y., ‘Fourier bases and Fourier frames on self-affine measures’, in: Conf. Fractals and Related Fields (Birkhauser, Cham, 2015), 87–111.Google Scholar
Fuglede, B., ‘Commuting self-adjoint partial differential operators and a group theoretic problem’, J. Funct. Anal. 16 (1974), 101–121.CrossRefGoogle Scholar
Hutchinson, J. B., ‘Fractals and self-similarity’, Indiana Univ. Math. J. 30 (1981), 713–747.10.1512/iumj.1981.30.30055CrossRefGoogle Scholar
Jones, G. A., Elementary Number Theory (Springer, London, 1998).CrossRefGoogle Scholar
Jorgensen, P. E. T., Kornelson, K. A. and Shuman, K. L., ‘An operator-fractal’, Numer. Funct. Anal. Optim. 33 (2012), 1070–1094.CrossRefGoogle Scholar
Jorgensen, P. E. T., Kornelson, K. A. and Shuman, K. L., ‘Scalar spectral measures associated with an operator-fractal’, J. Math. Phys. 55(2) (2014), 022103.CrossRefGoogle Scholar
Jorgensen, P. E. T., Kornelson, K. A. and Shuman, K. L., ‘Scaling by 5 on a [[()[]mml:mfrac[]()]][[()[]mml:mrow []()]]1[[()[]/mml:mrow[]()]] [[()[]mml:mrow []()]]4[[()[]/mml:mrow[]()]][[()[]/mml:mfrac[]()]]-Cantor measure’, Rocky Mountain J. Math. 44 (2014), 1881–1901.CrossRefGoogle Scholar
Jorgensen, P. E. T. and Pedersen, S., ‘Dense analytic subspaces in fractal L 2 -spaces’, J. Anal. Math. 75 (1998), 185–228.10.1007/BF02788699CrossRefGoogle Scholar
Łaba, I. and Wang, Y., ‘On spectral Cantor measures’, J. Funct. Anal. 193 (2002), 409–420.10.1006/jfan.2001.3941CrossRefGoogle Scholar
Liu, J. C. and Luo, J. J., ‘Spectral property of self-affine measure on ℝn’, J. Funct. Anal. 272 (2017), 599–612.CrossRefGoogle Scholar
Strichartz, R., ‘Mock Fourier series and transforms associated with certain Cantor measures’, J. Anal. Math. 81 (2000), 209–238.10.1007/BF02788990CrossRefGoogle Scholar
Tao, T., ‘Fuglede’s conjecture is false in 5 and higher dimensions’, Math. Res. Lett. 11(2–3) (2004), 251–258.CrossRefGoogle Scholar
Wang, Z. M., Dong, X. H. and Ai, W.-H., ‘Scaling of spectra of self-similar measures on ℝ’, Math. Nachr. 292(10) (2019), 2300–2307.CrossRefGoogle Scholar
Wu, Z. Y. and Zhu, M., ‘Scaling of spectra of self-similar measures with consecutive digits’, J. Math. Anal. Appl. 459(1) (2018), 307–319.CrossRefGoogle Scholar