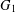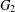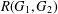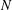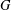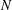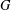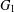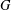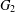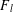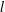Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Guantao
Yu, Xiaowei
and
Zhao, Yi
2021.
Improved bounds on the Ramsey number of fans.
European Journal of Combinatorics,
Vol. 96,
Issue. ,
p.
103347.
Wang, Maoqun
and
Qian, Jianguo
2022.
Ramsey Numbers for Complete Graphs Versus Generalized Fans.
Graphs and Combinatorics,
Vol. 38,
Issue. 6,
Dvořák, Vojtěch
and
Metrebian, Harry
2023.
A new upper bound for the Ramsey number of fans.
European Journal of Combinatorics,
Vol. 110,
Issue. ,
p.
103680.