Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-19T03:14:09.346Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON POWERFUL NUMBERS IN SHORT INTERVALS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  22 September 2022

TSZ HO CHAN Open the ORCID record for TSZ HO CHAN [Opens in a new window]
TSZ HO CHAN*
Affiliation:
Mathematics Department, Kennesaw State University, Marietta, GA 30060, USA
*
e-mail: tchan4@kennesaw.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate uniform upper bounds for the number of powerful numbers in short intervals 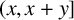$(x, x + y]$. We obtain unconditional upper bounds $O({y}/{\log y})$ and 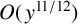$O(\kern1.3pt y^{11/12})$ for all powerful numbers and 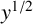$y^{1/2}$-smooth powerful numbers, respectively. Conditional on the 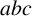$abc$-conjecture, we prove the bound $O({y}/{\log ^{1+\epsilon } y})$ for squarefull numbers and the bound 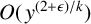$O(\kern1.3pt y^{(2 + \epsilon )/k})$ for k-full numbers when 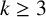$k \ge 3$. These bounds are related to Roth’s theorem on arithmetic progressions and the conjecture on the nonexistence of three consecutive squarefull numbers.

Keywords

powerful numbersBrun–Titchmarsh inequalityabc-conjectureRoth’s theorem on arithmetic progressions

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 99 - 106
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bateman, P. T. and Grosswald, E., ‘On a theorem of Erdős and Szekeres’, Illinois J. Math. 2 (1958), 88–98.CrossRefGoogle Scholar
Bloom, T. F. and Sisask, O., ‘Breaking the logarithmic barrier in Roth’s theorem on arithmetic progressions’, Preprint, 2021, arXiv:2007.03528.Google Scholar
De Koninck, J. M., Luca, F. and Shparlinski, I. E., ‘Powerful numbers in short intervals’, Bull. Aust. Math. Soc. 71(1) (2005), 11–16.CrossRefGoogle Scholar
Erdős, P. and Szekeres, G., ‘Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem’, Acta Univ. Szeged 7 (1934–1935), 95–102.Google Scholar
Halberstam, H. and Richert, H. E., Sieve Methods, London Mathematical Society Monographs, 4 (Academic Press [Harcourt Brace Jovanovich, Publishers], London–New York, 1974).Google Scholar
Liu, H. Q., ‘The number of cubefull numbers in an interval’, Funct. Approx. Comment. Math. 43(2) (2010), 105–107.CrossRefGoogle Scholar
Shiu, P., ‘A Brun–Titchmarsh theorem for multiplicative functions’, J. reine angew. Math. 313 (1980), 161–170.Google Scholar
Trifonov, O., ‘Lattice points close to a smooth curve and squarefull numbers in short intervals’, J. Lond. Math. Soc. (2) 65 (2002), 303–319.CrossRefGoogle Scholar