Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yao, Yonghong
Liou, Yeong-Cheng
and
Wu, Yuh-Jenn
2009.
An Extragradient Method for Mixed Equilibrium Problems and Fixed Point Problems.
Fixed Point Theory and Applications,
Vol. 2009,
Issue. 1,
Yao, Yonghong
and
Liou, YeongCheng
2010.
An Implicit Extragradient Method for Hierarchical Variational Inequalities.
Fixed Point Theory and Applications,
Vol. 2011,
Issue. 1,
Yao, Yonghong
Liou, Yeong-Cheng
and
Chen, Chia-Ping
2010.
Hierarchical Convergence of a Double-Net Algorithm for Equilibrium Problems and Variational Inequality Problems.
Fixed Point Theory and Applications,
Vol. 2010,
Issue. 1,
Yao, Yonghong
Marino, Giuseppe
and
Liou, Yeong-Cheng
2011.
A Hybrid Method for Monotone Variational Inequalities Involving Pseudocontractions.
Fixed Point Theory and Applications,
Vol. 2011,
Issue. 1,
Yao, Yonghong
Je Cho, Yeol
and
Liou, Yeong-Cheng
2011.
Hierarchical convergence of an implicit double-net algorithm for nonexpansive semigroups and variational inequality problems.
Fixed Point Theory and Applications,
Vol. 2011,
Issue. 1,
Yao, Yonghong
Cho, Yeol Je
Yang, Pei-Xia
and
Marino, Giuseppe
2012.
An Iterative Algorithm for a Hierarchical Problem.
Journal of Applied Mathematics,
Vol. 2012,
Issue. 1,
Sahu, D. R.
Colao, V.
and
Marino, G.
2013.
Strong convergence theorems for approximating common fixed points of families of nonexpansive mappings and applications.
Journal of Global Optimization,
Vol. 56,
Issue. 4,
p.
1631.
Wairojjana, Nopparat
and
Kumam, Poom
2014.
Existence and Algorithm for the Systems of Hierarchical Variational Inclusion Problems.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Yao, Zhangsong
Liou, Yeong-Cheng
Zhu, Li-Jun
Lo, Ching-Hua
and
Wu, Chen-Chang
2015.
Strong convergence theorems for fixed point problems, variational inequality problems, and equilibrium problems.
Journal of Inequalities and Applications,
Vol. 2015,
Issue. 1,
Wairojjana, N.
and
Kumam, P.
2016.
Some Existence and Convergence Theorems for Solving a System of Hierarchical Optimization Problems.
Computational Mathematics and Modeling,
Vol. 27,
Issue. 2,
p.
228.
Kazmi, K. R.
Ali, Rehan
and
Furkan, Mohd
2018.
Hybrid iterative method for split monotone variational inclusion problem and hierarchical fixed point problem for a finite family of nonexpansive mappings.
Numerical Algorithms,
Vol. 79,
Issue. 2,
p.
499.
Kazmi, K. R.
Ali, Rehan
and
Furkan, Mohd
2018.
Krasnoselski-Mann type iterative method for hierarchical fixed point problem and split mixed equilibrium problem.
Numerical Algorithms,
Vol. 77,
Issue. 1,
p.
289.
Kazmi, K. R.
Ali, Rehan
Yousuf, Saleem
and
Shahzad, Mohammad
2019.
A hybrid iterative algorithm for solving monotone variational inclusion and hierarchical fixed point problems.
Calcolo,
Vol. 56,
Issue. 4,
Kim, Jong Kyu
and
Majee, Prashanta
2020.
Modified Krasnoselski–Mann iterative method for hierarchical fixed point problem and split mixed equilibrium problem.
Journal of Inequalities and Applications,
Vol. 2020,
Issue. 1,
Wen, Dao-Jun
2021.
Modified Krasnoselski–Mann type iterative algorithm with strong convergence for hierarchical fixed point problem and split monotone variational inclusions.
Journal of Computational and Applied Mathematics,
Vol. 393,
Issue. ,
p.
113501.
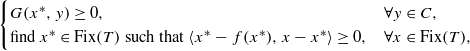 where C is a closed convex subset of a Hilbert space H, G:C×C→ℝ is an equilibrium function, T:C→C is a nonexpansive mapping with Fix(T) its set of fixed points and f:C→C is a ρ-contraction. Our algorithm is constructed and proved using the idea of the paper of [Y. Yao and Y.-C. Liou, ‘Weak and strong convergence of Krasnosel’skiĭ–Mann iteration for hierarchical fixed point problems’, Inverse Problems24 (2008), 501–508], in which only the variational inequality problem of finding hierarchically a fixed point of a nonexpansive mapping T with respect to a ρ-contraction f was considered. The paper follows the lines of research of corresponding results of Moudafi and Théra.
where C is a closed convex subset of a Hilbert space H, G:C×C→ℝ is an equilibrium function, T:C→C is a nonexpansive mapping with Fix(T) its set of fixed points and f:C→C is a ρ-contraction. Our algorithm is constructed and proved using the idea of the paper of [Y. Yao and Y.-C. Liou, ‘Weak and strong convergence of Krasnosel’skiĭ–Mann iteration for hierarchical fixed point problems’, Inverse Problems24 (2008), 501–508], in which only the variational inequality problem of finding hierarchically a fixed point of a nonexpansive mapping T with respect to a ρ-contraction f was considered. The paper follows the lines of research of corresponding results of Moudafi and Théra.

