Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rabinowitz, Philip
and
Smith, William E.
1987.
Interpolatory product integration for Riemann-integrable functions.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 29,
Issue. 2,
p.
195.
Vermiglio, Rossana
2017.
Polynomial Chaos Expansions for the Stability Analysis of Uncertain Delay Differential Equations.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 5,
Issue. 1,
p.
278.


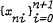 denote the zeros of (1−
denote the zeros of (1−