Article contents
RECOVERY OF THE TEMPERATURE DISTRIBUTION IN A MULTILAYER FRACTIONAL DIFFUSION EQUATION
Published online by Cambridge University Press: 20 February 2019
Abstract
We study the inverse boundary value problem for fractional diffusion in a multilayer composite medium. Given data in the right boundary of the second layer, the problem is to recover the temperature distribution in the first layer, which is inaccessible for measurement. The problem is ill-posed and we propose a Fourier spectral approach to achieve Hölder approximations. The convergence analysis is performed in both the 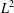 $L^{2}$- and
$L^{2}$- and 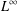 $L^{\infty }$-settings.
$L^{\infty }$-settings.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 344 - 352
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant no. 101.02-2018.312.
References
- 1
- Cited by


