Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-25T20:35:06.077Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LONGEST BLOCK FUNCTION IN CONTINUED FRACTIONS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  13 February 2020

TENG SONG Open the ORCID record for TENG SONG [Opens in a new window]  and
QINGLONG ZHOU Open the ORCID record for QINGLONG ZHOU [Opens in a new window]
TENG SONG
Affiliation:
School of Mathematics and Statistics,Huazhong University of Science and Technology, Wuhan, PR China email teng_song@hust.edu.cn
QINGLONG ZHOU*
Affiliation:
School of Mathematics and Statistics,Huazhong University of Science and Technology, Wuhan, PR China email qinglong_zhou@hust.edu.cn
*
✉qinglong_zhou@hust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

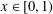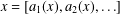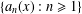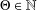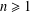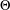For an irrational number $x\in [0,1)$, let $x=[a_{1}(x),a_{2}(x),\ldots ]$ be its continued fraction expansion with partial quotients $\{a_{n}(x):n\geq 1\}$. Given $\unicode[STIX]{x1D6E9}\in \mathbb{N}$, for $n\geq 1$, the $n$th longest block function of $x$ with respect to $\unicode[STIX]{x1D6E9}$ is defined by 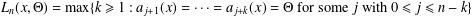$L_{n}(x,\unicode[STIX]{x1D6E9})=\max \{k\geq 1:a_{j+1}(x)=\cdots =a_{j+k}(x)=\unicode[STIX]{x1D6E9}~\text{for some}~j~\text{with}~0\leq j\leq n-k\}$, which represents the length of the longest consecutive sequence whose elements are all 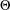$\unicode[STIX]{x1D6E9}$ from the first $n$ partial quotients of $x$. We consider the growth rate of 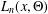$L_{n}(x,\unicode[STIX]{x1D6E9})$ as 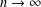$n\rightarrow \infty$ and calculate the Hausdorff dimensions of the level sets and exceptional sets arising from the longest block function.

Keywords

continued fractionlongest block functionHausdorff dimension

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 11J83: Metric theory 28A80: Fractals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 196 - 206
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by NSFC Grant No. 11431007.

References

Bakhtawar, A., Bos, P. and Hussain, M., ‘The sets of Dirichlet non-improvable numbers vs well-approximable numbers’, Preprint, 2018, arXiv:1806.00618.CrossRefGoogle Scholar
Bugeaud, Y. and Wang, B. W., ‘Distribution of full cylinders and the Diophantine properties of the orbits in 𝛽-expansions’, J. Fractal Geom. 1(2) (2014), 221–241.CrossRefGoogle Scholar
Chang, J. H. and Chen, H. B., ‘Slow increasing functions and the largest partial quotients in continued fraction expansions’, Math. Proc. Cambridge Philos. Soc. 164(1) (2018), 1–14.CrossRefGoogle Scholar
Erdős, P. and Rényi, A., ‘On a new law of large numbers’, J. Analyse Math. 23 (1970), 103–111.CrossRefGoogle Scholar
Falconer, K. J., Fractal Geometry. Mathematical Foundations and Applications, 3rd edn (Wiley, Chichester, 2014).Google Scholar
Ge, Y. H. and Lü, F., ‘A note on inhomogeneous Diophantine approximation in beta-dynamical system’, Bull. Aust. Math. Soc. 91(1) (2015), 34–40.CrossRefGoogle Scholar
Good, I. J., ‘The fractional dimensional theory of continued fractions’, Proc. Cambridge Philos. Soc. 37 (1941), 199–228.CrossRefGoogle Scholar
Huang, L. L. and Wu, J., ‘Uniformly non-improvable Dirichlet set via continued fractions’, Proc. Amer. Math. Soc. 147(11) (2019), 4617–4624.CrossRefGoogle Scholar
Hussain, M., Kleinbock, D., Wadleigh, N. and Wang, B. W., ‘Hausdorff measure of sets of Dirichlet non-improvable numbers’, Mathematika 64(2) (2018), 502–518.CrossRefGoogle Scholar
Jarník, V., ‘Zur metrischen Theorie der diophantischen Approximationen’, Prace Mat. Fiz. 36 (1929), 91–106.Google Scholar
Khintchine, A. Ya., Continued Fractions (Noordhoff, Groningen, 1963), translated by Peter Wynn.Google Scholar
Liu, J., Lü, M. Y. and Zhang, Z. L., ‘On the exceptional sets in Erdős–Rényi limit theorem of 𝛽-expansion’, Int. J. Number Theory 14(7) (2018), 1919–1934.CrossRefGoogle Scholar
Ma, J. H., Wen, S. Y. and Wen, Z. Y., ‘Egoroff’s theorem and maximal run length’, Monatsh. Math. 151(4) (2007), 287–292.CrossRefGoogle Scholar
Peng, L., Tan, B. and Wang, B. W., ‘Quantitative Poincaré recurrence in continued fraction dynamical system’, Sci. China Math. 55(1) (2012), 131–140.CrossRefGoogle Scholar
Philipp, W., ‘Some metrical theorems in number theory’, Pacific J. Math. 20 (1967), 109–127.CrossRefGoogle Scholar
Révész, P., Random Walk in Random and Non-Random Environments, 2nd edn (World Scientific, Hackensack, NJ, 2005).CrossRefGoogle Scholar
Sun, Y. and Xu, J., ‘A remark on exceptional sets in Erdős–Rényi limit theorem’, Monatsh. Math. 184(2) (2017), 291–296.CrossRefGoogle Scholar
Tan, B. and Zhou, Q. L., ‘The relative growth rate for partial quotients in continued fractions’, J. Math. Anal. Appl. 478(1) (2019), 229–235.CrossRefGoogle Scholar
Tong, X., Yu, Y. L. and Zhao, Y. F., ‘On the maximal length of consecutive zero digits of 𝛽-expansions’, Int. J. Number Theory 12(3) (2016), 625–633.CrossRefGoogle Scholar
Wang, B. W. and Wu, J., ‘On the maximal run-length function in continued fractions’, Ann. Univ. Sci. Budapest. Sect. Comput. 34 (2011), 247–268.Google Scholar
Wu, J., ‘A remark on the growth of the denominators of convergents’, Monatsh. Math. 147(3) (2006), 259–264.CrossRefGoogle Scholar
Zhou, Q. L., ‘Dimensions of recurrent sets in 𝛽-symbolic dynamics’, J. Math. Anal. Appl. 472(2) (2019), 1762–1776.CrossRefGoogle Scholar