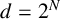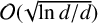1 Introduction
For
![]() $t \in [0,1]$
, let
$t \in [0,1]$
, let
![]() $B(t) = B(\omega )(t)$
denote the standard Brownian motion on a probability space
$B(t) = B(\omega )(t)$
denote the standard Brownian motion on a probability space
![]() $(\Omega ,\mathcal {F},P)$
. That is, for each
$(\Omega ,\mathcal {F},P)$
. That is, for each
![]() $t \in [0,1]$
,
$t \in [0,1]$
,
![]() $B(t)$
is a zero-mean Gaussian random variable, and for each pair
$B(t)$
is a zero-mean Gaussian random variable, and for each pair
![]() $t,s\in [0,1]$
the covariance is
$t,s\in [0,1]$
the covariance is
![]() $\mathbb {E}[B(t)B(s)] = \min (t,s)$
.
$\mathbb {E}[B(t)B(s)] = \min (t,s)$
.
In this paper we are concerned with the Lévy–Ciesielski (or Brownian bridge) construction of the Brownian paths. The Lévy–Ciesielski construction expresses the Brownian path
![]() $B(t)$
in terms of a Faber–Schauder basis
$B(t)$
in terms of a Faber–Schauder basis
![]() $\{ \eta _0, \eta _{n,i} : n\in \mathbb {N}, i=1,\ldots , 2^{n-1}\}$
of continuous functions on
$\{ \eta _0, \eta _{n,i} : n\in \mathbb {N}, i=1,\ldots , 2^{n-1}\}$
of continuous functions on
![]() $[0,1]$
, where
$[0,1]$
, where
![]() $\eta _0(t) := t$
and
$\eta _0(t) := t$
and
 $$ \begin{align*} \eta_{n,i}(t) := \begin{cases} \displaystyle 2^{(n-1)/2} \bigg(t-\frac{2i-2}{2^n}\bigg), &\displaystyle t\in \bigg[\frac{2i-2}{2^n}, \frac{2i-1}{2^n}\bigg],\\ \displaystyle 2^{(n-1)/2} \bigg(\frac{2i}{2^n}-t\bigg), &\displaystyle t\in \bigg[\frac{2i-1}{2^n}, \frac{2i}{2^n}\bigg],\\ 0,& \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \eta_{n,i}(t) := \begin{cases} \displaystyle 2^{(n-1)/2} \bigg(t-\frac{2i-2}{2^n}\bigg), &\displaystyle t\in \bigg[\frac{2i-2}{2^n}, \frac{2i-1}{2^n}\bigg],\\ \displaystyle 2^{(n-1)/2} \bigg(\frac{2i}{2^n}-t\bigg), &\displaystyle t\in \bigg[\frac{2i-1}{2^n}, \frac{2i}{2^n}\bigg],\\ 0,& \mbox{otherwise}. \end{cases} \end{align*} $$
For a proof that this is a basis in
![]() $\mathcal {C}[0,1]$
, see [Reference Triebel9, Theorem 2.1(iii)] or [Reference Triebel10]. In this construction, the Brownian path corresponding to the sample point
$\mathcal {C}[0,1]$
, see [Reference Triebel9, Theorem 2.1(iii)] or [Reference Triebel10]. In this construction, the Brownian path corresponding to the sample point
![]() $\omega \in \Omega $
is given by
$\omega \in \Omega $
is given by
 $$ \begin{align} B(t) := X_0(\omega)\, \eta_0(t) +\sum_{n=1}^\infty \sum_{i=1}^{2^{n-1}} X_{n,i}(\omega)\,\eta_{n,i}(t), \end{align} $$
$$ \begin{align} B(t) := X_0(\omega)\, \eta_0(t) +\sum_{n=1}^\infty \sum_{i=1}^{2^{n-1}} X_{n,i}(\omega)\,\eta_{n,i}(t), \end{align} $$
where
![]() $X_0$
and all the
$X_0$
and all the
![]() $X_{n,i}, i=1,\ldots ,2^{n-1},n\in \mathbb {N}$
, are independent standard normal random variables. For
$X_{n,i}, i=1,\ldots ,2^{n-1},n\in \mathbb {N}$
, are independent standard normal random variables. For
![]() $N \in \mathbb {N}$
we define the truncated Lévy–Ciesielski expansion by
$N \in \mathbb {N}$
we define the truncated Lévy–Ciesielski expansion by
 $$ \begin{align} B_{N}(t) := X_0(\omega)\,\eta_0(t) + \sum_{n=1}^N \sum_{i=1}^{2^{n-1}} X_{n,i}(\omega)\,\eta_{n,i}(t). \end{align} $$
$$ \begin{align} B_{N}(t) := X_0(\omega)\,\eta_0(t) + \sum_{n=1}^N \sum_{i=1}^{2^{n-1}} X_{n,i}(\omega)\,\eta_{n,i}(t). \end{align} $$
Then
![]() $B_{N}(t)$
is for each
$B_{N}(t)$
is for each
![]() $\omega \in \Omega $
a piecewise-linear function of t coinciding with
$\omega \in \Omega $
a piecewise-linear function of t coinciding with
![]() $B(t)$
at special values of t: we easily see that
$B(t)$
at special values of t: we easily see that
![]() $B(0)=B_N(0)=0$
,
$B(0)=B_N(0)=0$
,
![]() $B(1) =B_N(1) = X_0$
and
$B(1) =B_N(1) = X_0$
and
because the terms in (1.1) with
![]() $n> N$
vanish at these points.
$n> N$
vanish at these points.
The Lévy–Ciesielski construction has the important property that it converges almost surely to a continuous Brownian path (see the original works [Reference Ciesielski2, Reference Lévy4] or [Reference Steele8]). The precise statement is that, almost surely,
The convergence rate for the expected uniform error of the Lévy–Ciesielski expansion was obtained in [Reference Ritter6, Theorem 2]: in the language of this paper,
 $$ \begin{align} \mathbb{E}[\|B-B_N\|_{\infty} ] \sim \sqrt{\frac{\ln d}{2d}}, \end{align} $$
$$ \begin{align} \mathbb{E}[\|B-B_N\|_{\infty} ] \sim \sqrt{\frac{\ln d}{2d}}, \end{align} $$
where
![]() $d := 1+\sum _{n=1}^N 2^{n-1} =2^N$
is the dimension of the Faber–Schauder basis to level N.
$d := 1+\sum _{n=1}^N 2^{n-1} =2^N$
is the dimension of the Faber–Schauder basis to level N.
The meaning of the expected value
![]() $\mathbb {E}$
will be made precise in Section 2. The asymptotic notation
$\mathbb {E}$
will be made precise in Section 2. The asymptotic notation
![]() $\alpha (x)\sim \beta (x)$
means that
$\alpha (x)\sim \beta (x)$
means that
![]() $\lim _{x\to \infty } |\alpha (x)/\beta (x)| \to 1$
. Thus, (1.3) gives the precise leading term for the expected uniform error of the Lévy–Ciesielski expansion. Actually, Ritter [Reference Ritter6] shows also that the Lévy–Ciesielski approximation is optimal among all constructions that use information at d points and Wiener measure. Müller-Gronbach [Reference Müller-Gronbach5] provides results for more general problems.
$\lim _{x\to \infty } |\alpha (x)/\beta (x)| \to 1$
. Thus, (1.3) gives the precise leading term for the expected uniform error of the Lévy–Ciesielski expansion. Actually, Ritter [Reference Ritter6] shows also that the Lévy–Ciesielski approximation is optimal among all constructions that use information at d points and Wiener measure. Müller-Gronbach [Reference Müller-Gronbach5] provides results for more general problems.
The main result of this paper is Theorem 1.1 below which gives upper bounds of the same order as (1.3), with a slightly worse constant which is larger by a factor of
![]() ${2+\sqrt {2} \approx 3.41421}$
. We prove this constructively in Section 3 using a different line of argument than [Reference Ritter6], namely extreme value statistics.
${2+\sqrt {2} \approx 3.41421}$
. We prove this constructively in Section 3 using a different line of argument than [Reference Ritter6], namely extreme value statistics.
Theorem 1.1. Let B be the Lévy–Ciesielski expansion of the standard Brownian motion (1.1) and let
![]() $B_N$
be the corresponding truncated expansion (1.2). Then, with
$B_N$
be the corresponding truncated expansion (1.2). Then, with
![]() $d = 2^N$
,
$d = 2^N$
,
 $$ \begin{align*} \mathbb{E}[\|B-B_N\|_\infty] &\le (2+\sqrt{2}) \sqrt{\frac{\ln d}{2d}} \bigg(1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln d}}\bigg)\bigg), \\ \sqrt{\mathbb{E}[\|B-B_N\|_\infty^2]} &\le (2+\sqrt{2}) \sqrt{\frac{\ln d}{2d}} \bigg(1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln d}}\bigg)\bigg). \end{align*} $$
$$ \begin{align*} \mathbb{E}[\|B-B_N\|_\infty] &\le (2+\sqrt{2}) \sqrt{\frac{\ln d}{2d}} \bigg(1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln d}}\bigg)\bigg), \\ \sqrt{\mathbb{E}[\|B-B_N\|_\infty^2]} &\le (2+\sqrt{2}) \sqrt{\frac{\ln d}{2d}} \bigg(1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln d}}\bigg)\bigg). \end{align*} $$
Geometric Brownian motion is the solution
![]() $S(t) = S(\omega )(t)$
at time t of the stochastic differential equation
$S(t) = S(\omega )(t)$
at time t of the stochastic differential equation
for given initial data
![]() $S(0)$
, where
$S(0)$
, where
![]() $r>0$
is the drift,
$r>0$
is the drift,
![]() $\sigma>0$
is the volatility and
$\sigma>0$
is the volatility and
![]() $B(t)$
is the standard Brownian motion. The solution to (1.4) is given explicitly by
$B(t)$
is the standard Brownian motion. The solution to (1.4) is given explicitly by
Let
![]() $S_N$
be the approximation defined by
$S_N$
be the approximation defined by
where
![]() $B_N$
is the truncated Lévy–Ciesielski approximation of B given by (1.2). Then we prove in Section 4 the following corollary to Theorem 1.1.
$B_N$
is the truncated Lévy–Ciesielski approximation of B given by (1.2). Then we prove in Section 4 the following corollary to Theorem 1.1.
Corollary 1.2. Let S be the geometric Brownian motion (1.5) and let
![]() $S_N$
be the truncated approximation (1.6). Then, with
$S_N$
be the truncated approximation (1.6). Then, with
![]() $d=2^N$
,
$d=2^N$
,
 $$ \begin{align*} \mathbb{E}[\|S - S_N \|_\infty] = \mathcal{O}\bigg(\sqrt{\frac{\ln d}{d}}\bigg), \end{align*} $$
$$ \begin{align*} \mathbb{E}[\|S - S_N \|_\infty] = \mathcal{O}\bigg(\sqrt{\frac{\ln d}{d}}\bigg), \end{align*} $$
where the implied constant depends only on r and
![]() $\sigma $
.
$\sigma $
.
Section 5 gives an application to the problem of pricing an arithmetic Asian option.
2 The expected value as an integral over a sequence space
In this section we show that the expected value in Theorem 1.1 can be expressed as an integral over a sequence space. We remark that we will sometimes find it convenient to use interchangeably the language of measure and integration or alternatively that of probability and expectation.
Recall that the Lévy–Ciesielski expansion (1.1) expresses the Brownian path
![]() $B(t)$
in terms of an infinite sequence
$B(t)$
in terms of an infinite sequence
![]() ${\mathbf {X}}(\omega )=(X_0, (X_{n,i})_{n\in \mathbb {N}, i=1,\ldots , 2^{n-1}})$
of independent standard normal random variables. In the following we will denote a particular realisation of this sequence
${\mathbf {X}}(\omega )=(X_0, (X_{n,i})_{n\in \mathbb {N}, i=1,\ldots , 2^{n-1}})$
of independent standard normal random variables. In the following we will denote a particular realisation of this sequence
![]() ${\mathbf {X}}$
by
${\mathbf {X}}$
by
where we will switch freely between the double-index labelling
![]() $(x_0,x_{1,1}, x_{2,1}, x_{2,2},\ldots )$
and a single-index labelling
$(x_0,x_{1,1}, x_{2,1}, x_{2,2},\ldots )$
and a single-index labelling
![]() $(x_0,x_1,x_2,x_3,\ldots )$
as appropriate, with the indexing convention that
$(x_0,x_1,x_2,x_3,\ldots )$
as appropriate, with the indexing convention that
![]() $x_{n,i}$
becomes
$x_{n,i}$
becomes
![]() $x_{2^{n-1}-1+i}$
for
$x_{2^{n-1}-1+i}$
for
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $1\le i\le 2^{n-1}$
.
$1\le i\le 2^{n-1}$
.
It is clear from (1.1) that, for
![]() $t\in [0,1]$
and a fixed
$t\in [0,1]$
and a fixed
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
 $$ \begin{align} | B_{N}(t)| & \le | X_0| + \sum_{n=1}^N \Big(\max_{1\le i\le 2^{n-1}} | X_{n,i}|\Big) \sum_{i=1}^{2^{n-1}}\eta_{n,i}(t) \le | X_0| + \sum_{n=1}^N \max_{1\le i\le 2^{n-1}} | X_{n,i}| 2^{-(n+1)/2}, \end{align} $$
$$ \begin{align} | B_{N}(t)| & \le | X_0| + \sum_{n=1}^N \Big(\max_{1\le i\le 2^{n-1}} | X_{n,i}|\Big) \sum_{i=1}^{2^{n-1}}\eta_{n,i}(t) \le | X_0| + \sum_{n=1}^N \max_{1\le i\le 2^{n-1}} | X_{n,i}| 2^{-(n+1)/2}, \end{align} $$
where in the last step we used the fact that for a given
![]() $n\geq 1$
the disjoint nature of the Faber–Schauder functions ensures that at most one value of i contributes to the sum over i, and also that the
$n\geq 1$
the disjoint nature of the Faber–Schauder functions ensures that at most one value of i contributes to the sum over i, and also that the
![]() $\eta _{n,i}$
for
$\eta _{n,i}$
for
![]() $i=1,\ldots ,2^{n-1}$
have the same maximum value
$i=1,\ldots ,2^{n-1}$
have the same maximum value
![]() $2^{-(n+1)/2}$
.
$2^{-(n+1)/2}$
.
Motivated by the bound (2.1), and following [Reference Griebel, Kuo and Sloan3], we define a norm of the sequence
![]() ${\mathbf {x}} = (x_0,(x_{n,i})_{n\in \mathbb {N}, i=1,\ldots ,2^{n-1}})$
by
${\mathbf {x}} = (x_0,(x_{n,i})_{n\in \mathbb {N}, i=1,\ldots ,2^{n-1}})$
by
 $$ \begin{align*} \|{\mathbf{x}}\|_{\mathcal{X}} := |x_0|+ \sum_{n=1}^\infty \max_{1\leq i \leq 2^{n-1}} |x_{n,i}|\, 2^{-(n+1)/2}, \end{align*} $$
$$ \begin{align*} \|{\mathbf{x}}\|_{\mathcal{X}} := |x_0|+ \sum_{n=1}^\infty \max_{1\leq i \leq 2^{n-1}} |x_{n,i}|\, 2^{-(n+1)/2}, \end{align*} $$
and we define a corresponding normed space by
![]() $\mathcal {X} := \{ {\mathbf {x}}\in \mathbb {R}^\infty : \|{\mathbf {x}}\|_{\mathcal {X}} < \infty \}$
. It is easily seen that
$\mathcal {X} := \{ {\mathbf {x}}\in \mathbb {R}^\infty : \|{\mathbf {x}}\|_{\mathcal {X}} < \infty \}$
. It is easily seen that
![]() $\mathcal {X}$
is a Banach space.
$\mathcal {X}$
is a Banach space.
Each choice of
![]() ${\mathbf {x}}\in \mathcal {X}$
corresponds to a particular
${\mathbf {x}}\in \mathcal {X}$
corresponds to a particular
![]() $\omega \in \Omega $
(but not vice versa, since there are sample points
$\omega \in \Omega $
(but not vice versa, since there are sample points
![]() $\omega \in \Omega $
corresponding to sequences
$\omega \in \Omega $
corresponding to sequences
![]() ${\mathbf {x}}$
for which the norm
${\mathbf {x}}$
for which the norm
![]() $\|{\mathbf {x}}\|_{\mathcal {X}}$
is not finite). Hence, to each
$\|{\mathbf {x}}\|_{\mathcal {X}}$
is not finite). Hence, to each
![]() ${\mathbf {x}}\in \mathcal {X}$
there corresponds a particular Brownian path via (1.1), or expressed in terms of
${\mathbf {x}}\in \mathcal {X}$
there corresponds a particular Brownian path via (1.1), or expressed in terms of
![]() ${\mathbf {x}}$
,
${\mathbf {x}}$
,
 $$ \begin{align} B({\mathbf{x}})(t) = x_0\, \eta_0(t) +\sum_{n=1}^\infty \sum_{i=1}^{2^{n-1}} x_{n,i}\, \eta_{n,i}(t),\quad t\in[0,1]. \end{align} $$
$$ \begin{align} B({\mathbf{x}})(t) = x_0\, \eta_0(t) +\sum_{n=1}^\infty \sum_{i=1}^{2^{n-1}} x_{n,i}\, \eta_{n,i}(t),\quad t\in[0,1]. \end{align} $$
That the resulting path is continuous on
![]() $[0,1]$
follows from the observation that the path is the pointwise limit of the truncated series
$[0,1]$
follows from the observation that the path is the pointwise limit of the truncated series
 $$ \begin{align} B_N({\mathbf{x}})(t) \,=\,x_0\, \eta_0(t) +\sum_{n=1}^N \sum_{i=1}^{2^{n-1}} x_{n,i}\, \eta_{n,i}(t),\quad t\in[0,1], \end{align} $$
$$ \begin{align} B_N({\mathbf{x}})(t) \,=\,x_0\, \eta_0(t) +\sum_{n=1}^N \sum_{i=1}^{2^{n-1}} x_{n,i}\, \eta_{n,i}(t),\quad t\in[0,1], \end{align} $$
which is uniformly convergent since
 $$ \begin{align*} \|B_N\|_\infty \,\le\, |x_0|+ \sum_{n=1}^\infty \max_{1\leq i \leq 2^{n-1}} |x_{n,i}| 2^{-(n+1)/2} = \|{\mathbf{x}}\|_{\mathcal{X}} \,<\, \infty \quad\mbox{for}\ {\mathbf{x}}\in\mathcal{X}, \end{align*} $$
$$ \begin{align*} \|B_N\|_\infty \,\le\, |x_0|+ \sum_{n=1}^\infty \max_{1\leq i \leq 2^{n-1}} |x_{n,i}| 2^{-(n+1)/2} = \|{\mathbf{x}}\|_{\mathcal{X}} \,<\, \infty \quad\mbox{for}\ {\mathbf{x}}\in\mathcal{X}, \end{align*} $$
so that (2.2) does indeed define a continuous function for
![]() ${\mathbf {x}}\in \mathcal {X}$
.
${\mathbf {x}}\in \mathcal {X}$
.
We define
![]() $\mathcal {A}_{\mathbb {R}^\infty }$
to be the
$\mathcal {A}_{\mathbb {R}^\infty }$
to be the
![]() $\sigma $
-algebra generated by products of Borel sets of
$\sigma $
-algebra generated by products of Borel sets of
![]() $\mathbb {R}$
(see [Reference Bogachev1, page 372]). On the Banach space
$\mathbb {R}$
(see [Reference Bogachev1, page 372]). On the Banach space
![]() $\mathcal {X}$
, we now define a product Gaussian measure
$\mathcal {X}$
, we now define a product Gaussian measure
![]() $\rho (d{\mathbf {x}}) := \otimes _{j=0}^\infty \phi (x_j) d x_j$
(see [Reference Bogachev1, page 392 and Example 2.35]), where
$\rho (d{\mathbf {x}}) := \otimes _{j=0}^\infty \phi (x_j) d x_j$
(see [Reference Bogachev1, page 392 and Example 2.35]), where
![]() $\phi $
is the standard normal probability density
$\phi $
is the standard normal probability density
![]() $\phi (x) := \exp (- x^2/2)/\sqrt {2\pi }$
.
$\phi (x) := \exp (- x^2/2)/\sqrt {2\pi }$
.
We next show that the space
![]() $\mathcal {X}$
has full Gaussian measure, that is,
$\mathcal {X}$
has full Gaussian measure, that is,
 $$ \begin{align*} \mathbb{P}\bigg(|X_0|+ \sum_{n=1}^\infty \max_{1\leq i\leq 2^{n-1}} |X_{n,i}| 2^{-(n+1)/2}<\infty\bigg) =1. \end{align*} $$
$$ \begin{align*} \mathbb{P}\bigg(|X_0|+ \sum_{n=1}^\infty \max_{1\leq i\leq 2^{n-1}} |X_{n,i}| 2^{-(n+1)/2}<\infty\bigg) =1. \end{align*} $$
This fact is the basis of the classical proof that the Lévy–Ciesielski construction almost surely converges uniformly to the Brownian path. For a brief explanation, we define
 $$ \begin{align*} H_n(\omega) := \begin{cases} |X_0(\omega)| & \mbox{for } n=0,\\ \max_{1\leq i\leq 2^{n-1}}|X_{n,i}(\omega)| 2^{-(n+1)/2} & \mbox{for } n \geq 1. \end{cases} \end{align*} $$
$$ \begin{align*} H_n(\omega) := \begin{cases} |X_0(\omega)| & \mbox{for } n=0,\\ \max_{1\leq i\leq 2^{n-1}}|X_{n,i}(\omega)| 2^{-(n+1)/2} & \mbox{for } n \geq 1. \end{cases} \end{align*} $$
As a consequence of the Borel–Cantelli lemma, one can construct a sequence
![]() $(\beta _n)_{n \geq 1}$
of positive numbers such that
$(\beta _n)_{n \geq 1}$
of positive numbers such that
 $$ \begin{align*} \sum_{n=1}^\infty \beta_n <\infty \quad\mbox{and}\quad \mathbb{P}(H_n(\cdot)> \beta_n \mbox{ infinitely often}) =0. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^\infty \beta_n <\infty \quad\mbox{and}\quad \mathbb{P}(H_n(\cdot)> \beta_n \mbox{ infinitely often}) =0. \end{align*} $$
We now define
![]() $\tilde \Omega $
to be the subset of
$\tilde \Omega $
to be the subset of
![]() $\Omega $
consisting of the sample points
$\Omega $
consisting of the sample points
![]() $\omega $
for which
$\omega $
for which
![]() $H_n(\omega )> \beta _n$
for only finitely many values of n. Then
$H_n(\omega )> \beta _n$
for only finitely many values of n. Then
![]() $\tilde \Omega $
is of full Gaussian measure and for each
$\tilde \Omega $
is of full Gaussian measure and for each
![]() $\omega \in \tilde \Omega $
there exists
$\omega \in \tilde \Omega $
there exists
![]() $N(\omega ) \in \mathbb {N}$
such that
$N(\omega ) \in \mathbb {N}$
such that
![]() $H_n(\omega ) \leq \beta _n$
for
$H_n(\omega ) \leq \beta _n$
for
![]() $n> N(\omega )$
, giving
$n> N(\omega )$
, giving
 $$ \begin{align*} \sum_{n=1}^{\infty} H_n(\omega) \le \sum_{n=1}^{N(\omega)} H_n(\omega) + \sum_{n=N(\omega)+1}^\infty \beta_n < \infty \quad \mbox{for}\; \omega \in \tilde \Omega. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty} H_n(\omega) \le \sum_{n=1}^{N(\omega)} H_n(\omega) + \sum_{n=N(\omega)+1}^\infty \beta_n < \infty \quad \mbox{for}\; \omega \in \tilde \Omega. \end{align*} $$
Thus,
![]() $\mathbb {P}(\sum _{n=0}^\infty H_n <\infty )=1$
as claimed and
$\mathbb {P}(\sum _{n=0}^\infty H_n <\infty )=1$
as claimed and
![]() $\mathcal {X}$
is of full Gaussian measure.
$\mathcal {X}$
is of full Gaussian measure.
We now study integration on the measure space
![]() $(\mathcal {X},\mathcal {A}_{\mathbb {R}^\infty },\rho )$
and we denote the integral, or the expected value, of a measurable function f by
$(\mathcal {X},\mathcal {A}_{\mathbb {R}^\infty },\rho )$
and we denote the integral, or the expected value, of a measurable function f by
![]() ${\mathbb {E}[f] := \int _{\mathcal {X}} f({\mathbf {x}}) \rho (d{\mathbf {x}})}$
.
${\mathbb {E}[f] := \int _{\mathcal {X}} f({\mathbf {x}}) \rho (d{\mathbf {x}})}$
.
3 Expected uniform error of standard Brownian motion
We devote this section to proving Theorem 1.1. We have, from (1.1) and (1.2),
 $$ \begin{align*} |B(t) - B_N(t)| = \bigg|\sum_{n=N+1}^\infty \sum_{i=1}^{2^{n-1}} X_{n,i} \eta_{n,i}(t) \bigg| \le \sum_{n=N+1}^\infty \bigg(\max_{1\le i\le 2^{n-1}} |X_{n,i}|\bigg) \sum_{i=1}^{2^{n-1}} \eta_{n,i}(t). \end{align*} $$
$$ \begin{align*} |B(t) - B_N(t)| = \bigg|\sum_{n=N+1}^\infty \sum_{i=1}^{2^{n-1}} X_{n,i} \eta_{n,i}(t) \bigg| \le \sum_{n=N+1}^\infty \bigg(\max_{1\le i\le 2^{n-1}} |X_{n,i}|\bigg) \sum_{i=1}^{2^{n-1}} \eta_{n,i}(t). \end{align*} $$
Using the same disjoint support argument as in (2.1), we conclude that
 $$ \begin{align*} \|B - B_N\|_\infty \le \sum_{n=N+1}^\infty \max_{1\le i\le 2^{n-1}} |X_{n,i}| 2^{-(n+1)/2} = \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{M_\ell}{2\sqrt{\ell}}, \end{align*} $$
$$ \begin{align*} \|B - B_N\|_\infty \le \sum_{n=N+1}^\infty \max_{1\le i\le 2^{n-1}} |X_{n,i}| 2^{-(n+1)/2} = \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{M_\ell}{2\sqrt{\ell}}, \end{align*} $$
where we introduced new random variables
Thus,
 $$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty ] \le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E}[M_\ell ]}{2\sqrt{\ell}}, \end{align} $$
$$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty ] \le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E}[M_\ell ]}{2\sqrt{\ell}}, \end{align} $$
and since
![]() $M_\ell $
and
$M_\ell $
and
![]() $M_{\ell '}$
are independent random variables for
$M_{\ell '}$
are independent random variables for
![]() $\ell \ne \ell '$
,
$\ell \ne \ell '$
,
 $$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty^2 ] &\le \sum_{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E} [M_\ell M_{\ell'}]}{2\sqrt{\ell}\cdot 2\sqrt{\ell'}} \nonumber\\ &= \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E}[M_\ell^2 ]}{2\sqrt{\ell}\cdot 2\sqrt{\ell}} + \sum_{\stackrel{\scriptstyle{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots}}{\scriptstyle{\ell\ne\ell'}}} \frac{\mathbb{E}[M_\ell]\, \mathbb{E}[M_{\ell'}]} {2\sqrt{\ell}\cdot 2\sqrt{\ell'}}. \end{align} $$
$$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty^2 ] &\le \sum_{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E} [M_\ell M_{\ell'}]}{2\sqrt{\ell}\cdot 2\sqrt{\ell'}} \nonumber\\ &= \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{\mathbb{E}[M_\ell^2 ]}{2\sqrt{\ell}\cdot 2\sqrt{\ell}} + \sum_{\stackrel{\scriptstyle{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots}}{\scriptstyle{\ell\ne\ell'}}} \frac{\mathbb{E}[M_\ell]\, \mathbb{E}[M_{\ell'}]} {2\sqrt{\ell}\cdot 2\sqrt{\ell'}}. \end{align} $$
Now we are in the territory of extreme value statistics. It is known that the distribution function of the maximum of the absolute value of
![]() $\ell $
independent and identical Gaussian random variables converges (after appropriate centring and scaling, as below) to the Gumbel distribution. A first step is to obtain an explicit expression for the distribution function of
$\ell $
independent and identical Gaussian random variables converges (after appropriate centring and scaling, as below) to the Gumbel distribution. A first step is to obtain an explicit expression for the distribution function of
![]() $M_\ell $
. Because
$M_\ell $
. Because
![]() $X_{n,1}, X_{n,2}, \ldots ,X_{n,\ell }$
are
$X_{n,1}, X_{n,2}, \ldots ,X_{n,\ell }$
are
![]() $\mathcal {N}(0,1)$
random variables, for
$\mathcal {N}(0,1)$
random variables, for
![]() $x\in \mathbb {R}^+$
and
$x\in \mathbb {R}^+$
and
![]() $i=1,\ldots ,\ell $
, we have
$i=1,\ldots ,\ell $
, we have
where
![]() $\phi $
is the standard normal density. Similarly,
$\phi $
is the standard normal density. Similarly,
 $$ \begin{align*} \mathbb{P}(|X_{n,i}|\le x) = \int_{-x}^x \phi(t)\,d t = \Phi(x) - \Phi(-x) = 2\Phi(x) - 1. \end{align*} $$
$$ \begin{align*} \mathbb{P}(|X_{n,i}|\le x) = \int_{-x}^x \phi(t)\,d t = \Phi(x) - \Phi(-x) = 2\Phi(x) - 1. \end{align*} $$
Therefore (since
![]() $X_{n,1}, X_{n,2}, \ldots ,X_{n,\ell }$
are independent random variables),
$X_{n,1}, X_{n,2}, \ldots ,X_{n,\ell }$
are independent random variables),
Thus, the distribution function of
![]() $M_\ell $
is
$M_\ell $
is
We now define a new random variable
![]() $Y_\ell $
for
$Y_\ell $
for
![]() $\ell \ge 1$
, which is a recentred and rescaled version of
$\ell \ge 1$
, which is a recentred and rescaled version of
![]() $M_\ell $
:
$M_\ell $
:
It is known (see below) to be appropriate to take
![]() $a_\ell $
and
$a_\ell $
and
![]() $b_\ell $
to satisfy
$b_\ell $
to satisfy
More precisely, for later convenience we will define
![]() $a_\ell $
to be the unique solution of
$a_\ell $
to be the unique solution of
 $$ \begin{align} \frac{1}{\ell} = \sqrt{\frac{2}{\pi}}\frac{e^{-a_\ell^2/2}}{a_\ell} =: g(a_\ell). \end{align} $$
$$ \begin{align} \frac{1}{\ell} = \sqrt{\frac{2}{\pi}}\frac{e^{-a_\ell^2/2}}{a_\ell} =: g(a_\ell). \end{align} $$
We now show that (3.6) implies (3.5).
Lemma 3.1. Equation (3.6) for
![]() $\ell \ge 1$
has a unique positive solution of the form
$\ell \ge 1$
has a unique positive solution of the form
![]() ${a_\ell =\sqrt {2\ln {\ell }}+o(1)}$
. Moreover, for
${a_\ell =\sqrt {2\ln {\ell }}+o(1)}$
. Moreover, for
![]() $\ell \ge 3$
we have
$\ell \ge 3$
we have
![]() $a_\ell \in (1,\sqrt {2\ln \ell })$
.
$a_\ell \in (1,\sqrt {2\ln \ell })$
.
Proof. The fact that any solution of (3.6) is positive is immediate. Now observe that g in (3.6) is monotonically decreasing from
![]() $+\infty $
to
$+\infty $
to
![]() $0$
on
$0$
on
![]() $\mathbb {R}^+$
. It follows immediately that there is a unique solution
$\mathbb {R}^+$
. It follows immediately that there is a unique solution
![]() $a_\ell \in (0,\infty )$
for (3.6). Moreover,
$a_\ell \in (0,\infty )$
for (3.6). Moreover,
 $$ \begin{align*} a_\ell> 1 \Leftrightarrow \frac{1}{\ell} < \sqrt {\frac 2 \pi }\frac {e^{-1^2/2}} {1} = \sqrt {\frac 2 {\pi e} } =0.484\ldots, \end{align*} $$
$$ \begin{align*} a_\ell> 1 \Leftrightarrow \frac{1}{\ell} < \sqrt {\frac 2 \pi }\frac {e^{-1^2/2}} {1} = \sqrt {\frac 2 {\pi e} } =0.484\ldots, \end{align*} $$
which holds if and only if
![]() $\ell \ge 3$
. Now observe that (3.6) is equivalent to
$\ell \ge 3$
. Now observe that (3.6) is equivalent to
 $$ \begin{align} a_\ell = \sqrt{ 2\left(\ln \ell - \ln \left(\sqrt {\frac \pi 2} a_\ell\right)\right)}. \end{align} $$
$$ \begin{align} a_\ell = \sqrt{ 2\left(\ln \ell - \ln \left(\sqrt {\frac \pi 2} a_\ell\right)\right)}. \end{align} $$
For
![]() $\ell \ge 3$
we have
$\ell \ge 3$
we have
![]() $a_\ell> 1$
and hence
$a_\ell> 1$
and hence
![]() $\ln (\sqrt {\pi /2}\,a_\ell )>\ln (\sqrt {\pi /2})>0$
, so from (3.7) we have
$\ln (\sqrt {\pi /2}\,a_\ell )>\ln (\sqrt {\pi /2})>0$
, so from (3.7) we have
![]() $a_\ell < \sqrt { 2 \ln \ell }$
. In turn it follows that
$a_\ell < \sqrt { 2 \ln \ell }$
. In turn it follows that
 $$ \begin{align*} a_\ell> \sqrt{2 \ln \ell - 2 \ln\bigg(\sqrt {\frac \pi 2 }\sqrt{2 \ln \ell}\bigg)}. \end{align*} $$
$$ \begin{align*} a_\ell> \sqrt{2 \ln \ell - 2 \ln\bigg(\sqrt {\frac \pi 2 }\sqrt{2 \ln \ell}\bigg)}. \end{align*} $$
Thus, for
![]() $\ell \ge 3$
we have
$\ell \ge 3$
we have
![]() $1\le a_\ell =\sqrt {2\ln \ell } +o(1) \le \sqrt {2\ln {\ell }}$
, completing the proof.
$1\le a_\ell =\sqrt {2\ln \ell } +o(1) \le \sqrt {2\ln {\ell }}$
, completing the proof.
It is well known that the distribution function of
![]() $Y_\ell $
converges in distribution to a random variable with the Gumbel distribution
$Y_\ell $
converges in distribution to a random variable with the Gumbel distribution
![]() $\exp (-e^{-y})$
. For later convenience we state this as a lemma and give a short proof.
$\exp (-e^{-y})$
. For later convenience we state this as a lemma and give a short proof.
Lemma 3.2. The random variable
![]() $Y_ \ell $
defined in (3.4), with
$Y_ \ell $
defined in (3.4), with
![]() $a_\ell $
defined by (3.6) and
$a_\ell $
defined by (3.6) and
![]() $b_\ell = 1/a_\ell $
, converges in distribution to a random variable Y with Gumbel distribution function
$b_\ell = 1/a_\ell $
, converges in distribution to a random variable Y with Gumbel distribution function
![]() $\mathbb {P}(Y\le y) = \exp (-e^{-y})$
.
$\mathbb {P}(Y\le y) = \exp (-e^{-y})$
.
Proof. The proof is based on the asymptotic version of Mill’s ratio [Reference Small7],
where, as in the Introduction,
![]() $\sim $
means that the quotient of the two sides converges to
$\sim $
means that the quotient of the two sides converges to
![]() $1$
. From this it follows that for
$1$
. From this it follows that for
![]() $y\in \mathbb {R}$
,
$y\in \mathbb {R}$
,
 $$ \begin{align*} \mathbb{P}(Y_\ell\le y) &=\mathbb{P}(M_\ell\le a_\ell+b_\ell y)\,=\,(2\Phi(a_\ell+b_\ell y)-1)^\ell =(1-2[1-\Phi(a_\ell+b_\ell y)])^\ell\\ &\sim\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}(a_\ell + b_\ell y)^2)}{a_\ell+b_\ell y}\bigg)^\ell \sim\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}a_\ell^2 - a_\ell b_\ell y)}{a_\ell}\bigg)^\ell \\ &=(1- \exp(-y)/\ell)^\ell \sim\exp(-e^{-y}) \quad \mbox{as} \ \ell\to\infty, \end{align*} $$
$$ \begin{align*} \mathbb{P}(Y_\ell\le y) &=\mathbb{P}(M_\ell\le a_\ell+b_\ell y)\,=\,(2\Phi(a_\ell+b_\ell y)-1)^\ell =(1-2[1-\Phi(a_\ell+b_\ell y)])^\ell\\ &\sim\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}(a_\ell + b_\ell y)^2)}{a_\ell+b_\ell y}\bigg)^\ell \sim\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}a_\ell^2 - a_\ell b_\ell y)}{a_\ell}\bigg)^\ell \\ &=(1- \exp(-y)/\ell)^\ell \sim\exp(-e^{-y}) \quad \mbox{as} \ \ell\to\infty, \end{align*} $$
where in the second step we dropped a higher-order term, and in the second last step we used (3.6) and
![]() $a_\ell b_\ell = 1$
, thus proving the lemma.
$a_\ell b_\ell = 1$
, thus proving the lemma.
A deeper result, which we need, is that
![]() $Y_\ell $
converges in expectation to the limit Y. This is proved in the following lemma.
$Y_\ell $
converges in expectation to the limit Y. This is proved in the following lemma.
Lemma 3.3. The random variable
![]() $Y_\ell $
defined in (3.4), with
$Y_\ell $
defined in (3.4), with
![]() $a_\ell $
defined by (3.6) and
$a_\ell $
defined by (3.6) and
![]() $b_\ell = 1/a_\ell $
, converges in expectation to a random variable Y with Gumbel distribution
$b_\ell = 1/a_\ell $
, converges in expectation to a random variable Y with Gumbel distribution
![]() $\exp (-e^{-y})$
, thus
$\exp (-e^{-y})$
, thus
where
![]() $\gamma $
is Euler’s constant.
$\gamma $
is Euler’s constant.
Proof. For a sequence of real-valued random variables
![]() $Y_1,Y_2,\ldots $
converging in distribution to a random variable Y, it is well known that a sufficient condition for convergence in expectation is uniform integrability of the
$Y_1,Y_2,\ldots $
converging in distribution to a random variable Y, it is well known that a sufficient condition for convergence in expectation is uniform integrability of the
![]() $Y_\ell $
. In turn a sufficient condition for uniform integrability is that for sufficiently large
$Y_\ell $
. In turn a sufficient condition for uniform integrability is that for sufficiently large
![]() $\ell $
,
$\ell $
,
where
![]() $Q(y)$
is integrable on
$Q(y)$
is integrable on
![]() $\mathbb {R}^+$
and
$\mathbb {R}^+$
and
![]() $R(y)$
is integrable on
$R(y)$
is integrable on
![]() $\mathbb {R}^-$
.
$\mathbb {R}^-$
.
First assume
![]() $y>0$
. From (3.3),
$y>0$
. From (3.3),
 $$ \begin{align*} \mathbb{P}(Y_\ell\ge y) &= \mathbb{P}(M_\ell\ge a_\ell + b_\ell y) = 1- \mathbb{P}(M_\ell\le a_\ell + b_\ell y) \\ &= 1- (2\Phi(a_\ell + b_\ell y)-1)^\ell = 1- (1 - 2[1-\Phi(a_\ell + b_\ell y)])^\ell \\ &\le 1-\bigg(1-2\frac{\phi(a_\ell + b_\ell y)}{a_\ell + b_\ell y}\bigg)^\ell =1-\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}(a_\ell + b_\ell y)^2)}{a_\ell + b_\ell y}\bigg)^\ell\\ &\le 1-\bigg(1-\sqrt{\frac{2}{\pi}}\frac{\exp(-\tfrac{1}{2}a_\ell^2 - a_\ell b_\ell y)} {a_\ell}\bigg)^\ell, \end{align*} $$
$$ \begin{align*} \mathbb{P}(Y_\ell\ge y) &= \mathbb{P}(M_\ell\ge a_\ell + b_\ell y) = 1- \mathbb{P}(M_\ell\le a_\ell + b_\ell y) \\ &= 1- (2\Phi(a_\ell + b_\ell y)-1)^\ell = 1- (1 - 2[1-\Phi(a_\ell + b_\ell y)])^\ell \\ &\le 1-\bigg(1-2\frac{\phi(a_\ell + b_\ell y)}{a_\ell + b_\ell y}\bigg)^\ell =1-\bigg(1-\sqrt{\frac{2}{\pi}} \frac{\exp(-\tfrac{1}{2}(a_\ell + b_\ell y)^2)}{a_\ell + b_\ell y}\bigg)^\ell\\ &\le 1-\bigg(1-\sqrt{\frac{2}{\pi}}\frac{\exp(-\tfrac{1}{2}a_\ell^2 - a_\ell b_\ell y)} {a_\ell}\bigg)^\ell, \end{align*} $$
where we used the upper bound form of Mills’s ratio [Reference Small7],
and dropped harmless terms in both the denominator and the exponent in the numerator. Using now (3.6) and also
![]() $a_\ell b_\ell = 1$
,
$a_\ell b_\ell = 1$
,
where we used the fact that the function
![]() $(1-c/x)^x$
is increasing on
$(1-c/x)^x$
is increasing on
![]() $[1,\infty )$
for
$[1,\infty )$
for
![]() $c\in [0,1]$
, and hence takes its minimum at
$c\in [0,1]$
, and hence takes its minimum at
![]() $x=1$
. It follows that
$x=1$
. It follows that
 $$ \begin{align*} \int_0^\infty \mathbb{P}(Y_\ell\ge y)\,d y \le \int_0^\infty \exp(-y)\,d y = 1. \end{align*} $$
$$ \begin{align*} \int_0^\infty \mathbb{P}(Y_\ell\ge y)\,d y \le \int_0^\infty \exp(-y)\,d y = 1. \end{align*} $$
Now we consider
![]() $y<0$
. Note first that
$y<0$
. Note first that
![]() $M_\ell =a_\ell +b_\ell Y_\ell $
takes only nonnegative values, thus we may restrict y to
$M_\ell =a_\ell +b_\ell Y_\ell $
takes only nonnegative values, thus we may restrict y to
![]() $y\ge -a_\ell /b_\ell $
. We have
$y\ge -a_\ell /b_\ell $
. We have
Now for
![]() $t>0$
the standard normal distribution
$t>0$
the standard normal distribution
![]() $\Phi $
has negative second derivative,
$\Phi $
has negative second derivative,
and first derivative
![]() $\Phi '(t)=\phi (t)$
, from which it follows that
$\Phi '(t)=\phi (t)$
, from which it follows that
Thus, on using
![]() $b_\ell =1/a_\ell $
, we obtain
$b_\ell =1/a_\ell $
, we obtain
 $$ \begin{align*} \mathbb{P}(Y_\ell\le y) &\le(2\Phi(a_\ell)+2a_\ell^{-1}y\phi(a_\ell)-1)^\ell\\ &\le(1-2a_\ell^{-1}\phi(a_\ell)(1-y-a_\ell^{-2}))^\ell =\bigg(1-\frac{1}{\ell}(1-y-a_\ell^{-2})\bigg)^\ell, \end{align*} $$
$$ \begin{align*} \mathbb{P}(Y_\ell\le y) &\le(2\Phi(a_\ell)+2a_\ell^{-1}y\phi(a_\ell)-1)^\ell\\ &\le(1-2a_\ell^{-1}\phi(a_\ell)(1-y-a_\ell^{-2}))^\ell =\bigg(1-\frac{1}{\ell}(1-y-a_\ell^{-2})\bigg)^\ell, \end{align*} $$
where in the second step we used the lower bound form of Mills’s ratio (see [Reference Small7, page 44]),
and in the last step we used (3.6). If we now take
![]() $\ell \ge L$
then
$\ell \ge L$
then
 $$ \begin{align} \mathbb{P}(Y_\ell\le y) &\le\bigg(1-\frac{1}{\ell}(1-y-a_L^{-2})\bigg)^\ell \nonumber\\ &\le \exp(-(1-y-a_L^{-2})) =\exp(-(1-a_L^{-2})) \exp(y) =: R(y), \end{align} $$
$$ \begin{align} \mathbb{P}(Y_\ell\le y) &\le\bigg(1-\frac{1}{\ell}(1-y-a_L^{-2})\bigg)^\ell \nonumber\\ &\le \exp(-(1-y-a_L^{-2})) =\exp(-(1-a_L^{-2})) \exp(y) =: R(y), \end{align} $$
since the convergence in the last limit is monotone increasing. The function
![]() $R(y)$
so defined is integrable on
$R(y)$
so defined is integrable on
![]() $\mathbb {R}^-$
, completing the proof that
$\mathbb {R}^-$
, completing the proof that
![]() $Y_\ell $
converges in expectation.
$Y_\ell $
converges in expectation.
It then follows from Lemma 3.2 that the limit of
![]() $\mathbb {E}[Y_\ell ]$
is precisely
$\mathbb {E}[Y_\ell ]$
is precisely
![]() $\mathbb {E}[Y] = \gamma $
.
$\mathbb {E}[Y] = \gamma $
.
Since Lemma 3.3 establishes the convergence of
![]() $\mathbb {E}[Y_\ell ]$
as
$\mathbb {E}[Y_\ell ]$
as
![]() $\ell \to \infty $
, it can be inferred that there exists a positive constant c such that
$\ell \to \infty $
, it can be inferred that there exists a positive constant c such that
where we used
![]() $b_\ell = a_\ell ^{-1} \le 1$
for
$b_\ell = a_\ell ^{-1} \le 1$
for
![]() $\ell \ge 3$
. We then conclude from (3.1) that
$\ell \ge 3$
. We then conclude from (3.1) that
 $$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty ] &\le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{a_\ell+c}{2\sqrt{\ell}}. \end{align} $$
$$ \begin{align} \mathbb{E}[ \|B - B_N\|_\infty ] &\le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{a_\ell+c}{2\sqrt{\ell}}. \end{align} $$
It only remains to estimate the sum in (3.11). Using Lemma 3.1 with
![]() $N\ge 2$
(and hence
$N\ge 2$
(and hence
![]() $\ell \ge 3$
), we have
$\ell \ge 3$
), we have
![]() $a_\ell < \sqrt {2\ln \ell }$
, and on setting
$a_\ell < \sqrt {2\ln \ell }$
, and on setting
![]() $\ell = 2^{N+j}$
,
$\ell = 2^{N+j}$
,
 $$ \begin{align*} \sum_{\ell=2^N, 2^{N+1}, 2^{N+2},\ldots}\frac{a_\ell}{\sqrt{\ell}} &\le \sum_{j=0}^\infty \frac {\sqrt{2(\ln 2) (N+j)}}{\sqrt{2^{N+j}}} = 2^{-(N-1)/2} \sqrt{\ln 2}\, \sum_{j=0}^\infty \frac {\sqrt{ N+j}}{2^{j/2}} .\nonumber \\ &\le 2^{-(N-1)/2} \sqrt{\ln 2}\,\sqrt{N}\,(2+\sqrt 2 )\,(1 + \mathcal{O}(N^{-1/2})), \nonumber \end{align*} $$
$$ \begin{align*} \sum_{\ell=2^N, 2^{N+1}, 2^{N+2},\ldots}\frac{a_\ell}{\sqrt{\ell}} &\le \sum_{j=0}^\infty \frac {\sqrt{2(\ln 2) (N+j)}}{\sqrt{2^{N+j}}} = 2^{-(N-1)/2} \sqrt{\ln 2}\, \sum_{j=0}^\infty \frac {\sqrt{ N+j}}{2^{j/2}} .\nonumber \\ &\le 2^{-(N-1)/2} \sqrt{\ln 2}\,\sqrt{N}\,(2+\sqrt 2 )\,(1 + \mathcal{O}(N^{-1/2})), \nonumber \end{align*} $$
where in the final step we used
![]() $\sqrt {N+j} \leq \sqrt {N}+\sqrt {j}$
and
$\sqrt {N+j} \leq \sqrt {N}+\sqrt {j}$
and
![]() $\sum _{j=0}^\infty 1/2^{j/2}=2+\sqrt {2}$
, while noting that
$\sum _{j=0}^\infty 1/2^{j/2}=2+\sqrt {2}$
, while noting that
![]() $\sum _{j=0}^\infty \sqrt {j}/2^{j/2}$
is finite and independent of N. Moreover, by a similar argument we conclude that
$\sum _{j=0}^\infty \sqrt {j}/2^{j/2}$
is finite and independent of N. Moreover, by a similar argument we conclude that
![]() $\sum _{\ell =2^N, 2^{N+1}, 2^{N+2},\ldots } c/\sqrt {\ell } = \mathcal {O}(2^{-N/2})$
. Thus, altogether we obtain from (3.11) that
$\sum _{\ell =2^N, 2^{N+1}, 2^{N+2},\ldots } c/\sqrt {\ell } = \mathcal {O}(2^{-N/2})$
. Thus, altogether we obtain from (3.11) that
 $$ \begin{align*} \mathbb{E}[ \|B - B_N\|_\infty ] & \le \tfrac{1}{2} \cdot 2^{-(N-1)/2}\sqrt{\ln2}\,\sqrt{N}\,(2+\sqrt{2})(1+\mathcal{O}(N^{-1/2})) \\ &= (2+\sqrt 2) \frac {\sqrt{N\ln{2}}}{\sqrt {2\cdot 2^{N}}}(1+\mathcal{O}(N^{-1/2})) = (2+\sqrt 2) \frac {\sqrt{\ln{d}}}{\sqrt {2 d}}\bigg (1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln{d}}}\bigg)\bigg), \end{align*} $$
$$ \begin{align*} \mathbb{E}[ \|B - B_N\|_\infty ] & \le \tfrac{1}{2} \cdot 2^{-(N-1)/2}\sqrt{\ln2}\,\sqrt{N}\,(2+\sqrt{2})(1+\mathcal{O}(N^{-1/2})) \\ &= (2+\sqrt 2) \frac {\sqrt{N\ln{2}}}{\sqrt {2\cdot 2^{N}}}(1+\mathcal{O}(N^{-1/2})) = (2+\sqrt 2) \frac {\sqrt{\ln{d}}}{\sqrt {2 d}}\bigg (1+\mathcal{O}\bigg(\frac{1}{\sqrt{\ln{d}}}\bigg)\bigg), \end{align*} $$
which proves the first bound in Theorem 1.1.
To prove the second bound in Theorem 1.1, we need first to bound
![]() $\mathbb {E}[M_\ell ^2]$
. With
$\mathbb {E}[M_\ell ^2]$
. With
![]() $Y_\ell $
and Y defined as above, for
$Y_\ell $
and Y defined as above, for
![]() $v>0$
,
$v>0$
,
 $$ \begin{align} \mathbb{P}(Y_\ell^2 \ge v) &= \mathbb{P}(Y_\ell \ge \sqrt{v}) + \mathbb{P}(Y_\ell \le - \sqrt{v}) \nonumber\\&\to \mathbb{P}(Y \ge \sqrt{v}) + \mathbb{P}(Y \le - \sqrt{v}) = \mathbb{P}(Y^2 \ge v) \quad\mbox{as}\ \ell\to\infty, \end{align} $$
$$ \begin{align} \mathbb{P}(Y_\ell^2 \ge v) &= \mathbb{P}(Y_\ell \ge \sqrt{v}) + \mathbb{P}(Y_\ell \le - \sqrt{v}) \nonumber\\&\to \mathbb{P}(Y \ge \sqrt{v}) + \mathbb{P}(Y \le - \sqrt{v}) = \mathbb{P}(Y^2 \ge v) \quad\mbox{as}\ \ell\to\infty, \end{align} $$
while for
![]() $v<0$
we have
$v<0$
we have
![]() $\mathbb {P}(Y_\ell ^2 \ge v) = \mathbb {P}(Y^2 \ge v)= 1$
. Thus, by Lemma 3.2,
$\mathbb {P}(Y_\ell ^2 \ge v) = \mathbb {P}(Y^2 \ge v)= 1$
. Thus, by Lemma 3.2,
![]() $Y_\ell ^2$
converges in distribution to
$Y_\ell ^2$
converges in distribution to
![]() $Y^2$
, where Y is the Gumbel distribution. To prove convergence in expectation, we use (3.12) with (3.8) and (3.9) to give, for
$Y^2$
, where Y is the Gumbel distribution. To prove convergence in expectation, we use (3.12) with (3.8) and (3.9) to give, for
![]() $\ell \ge L$
and
$\ell \ge L$
and
![]() $v>0$
,
$v>0$
,
which is integrable on
![]() $\mathbb {R}^+$
, proving
$\mathbb {R}^+$
, proving
![]() $\mathbb {E}[Y_\ell ^2] \to \mathbb {E}[Y^2] < \infty $
. In turn it follows that there exists
$\mathbb {E}[Y_\ell ^2] \to \mathbb {E}[Y^2] < \infty $
. In turn it follows that there exists
![]() $c'>0$
such that
$c'>0$
such that
![]() $\mathbb {E}[Y_\ell ^2] \le c'$
, and together with (3.10),
$\mathbb {E}[Y_\ell ^2] \le c'$
, and together with (3.10),
where we used
![]() $b_\ell = a_{\ell }^{-1} \le 1$
for
$b_\ell = a_{\ell }^{-1} \le 1$
for
![]() $\ell \ge 3$
and introduced
$\ell \ge 3$
and introduced
![]() $c" := \max (c,\sqrt {c'})$
. Now from (3.2),
$c" := \max (c,\sqrt {c'})$
. Now from (3.2),
 $$ \begin{align*} \mathbb{E}[ \|B - B_N\|_\infty^2 ] &\le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{(a_\ell + c")^2}{2\sqrt{\ell}\cdot 2\sqrt{\ell}} + \sum_{\stackrel{\scriptstyle{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots}}{\scriptstyle{\ell\ne\ell'}}} \frac{(a_\ell + c")(a_{\ell'} + c")}{2\sqrt{\ell}\cdot 2\sqrt{\ell'}} \\ &= \bigg(\sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{a_\ell + c"}{2\sqrt{\ell}}\bigg)^2, \end{align*} $$
$$ \begin{align*} \mathbb{E}[ \|B - B_N\|_\infty^2 ] &\le \sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{(a_\ell + c")^2}{2\sqrt{\ell}\cdot 2\sqrt{\ell}} + \sum_{\stackrel{\scriptstyle{\ell,\ell' = 2^{N}, 2^{N+1},2^{N+2},\ldots}}{\scriptstyle{\ell\ne\ell'}}} \frac{(a_\ell + c")(a_{\ell'} + c")}{2\sqrt{\ell}\cdot 2\sqrt{\ell'}} \\ &= \bigg(\sum_{\ell = 2^{N}, 2^{N+1},2^{N+2},\ldots} \frac{a_\ell + c"}{2\sqrt{\ell}}\bigg)^2, \end{align*} $$
which is the square of the right-hand side of (3.11), with c replaced by
![]() $c"$
. The second bound in Theorem 1.1 then follows.
$c"$
. The second bound in Theorem 1.1 then follows.
4 Expected uniform error of geometric Brownian motion
We can now give a proof of Corollary 1.2. From (1.5) and (1.6),
![]() $S(t) - S_N(t) = S(0) e^{(r-\sigma ^2/2)t}\, (\exp (\sigma B(t)) -\exp (\sigma B_N(t)))$
, and thus
$S(t) - S_N(t) = S(0) e^{(r-\sigma ^2/2)t}\, (\exp (\sigma B(t)) -\exp (\sigma B_N(t)))$
, and thus
In turn it follows that
 $$ \begin{align*} \|S - S_N\|_\infty &\le S(0)\,e^{|r-\sigma^2/2|}\, \|\exp(\sigma B_N) (\exp(\sigma (B-B_N)) - 1)\|_\infty \nonumber\\ &\le S(0)\,e^{|r-\sigma^2/2|}\, \exp(\sigma \|B_N\|_\infty) (\exp(\sigma \|B-B_N\|_\infty) - 1). \end{align*} $$
$$ \begin{align*} \|S - S_N\|_\infty &\le S(0)\,e^{|r-\sigma^2/2|}\, \|\exp(\sigma B_N) (\exp(\sigma (B-B_N)) - 1)\|_\infty \nonumber\\ &\le S(0)\,e^{|r-\sigma^2/2|}\, \exp(\sigma \|B_N\|_\infty) (\exp(\sigma \|B-B_N\|_\infty) - 1). \end{align*} $$
Using
![]() $|{\exp} (x)-1| \le |x| \exp (|x|)$
for
$|{\exp} (x)-1| \le |x| \exp (|x|)$
for
![]() $x\in \mathbb {R}$
and
$x\in \mathbb {R}$
and
![]() $\|B_N\|_\infty \le \|B\|_\infty $
for
$\|B_N\|_\infty \le \|B\|_\infty $
for
![]() $N\in \mathbb {N}$
, we have
$N\in \mathbb {N}$
, we have
 $$ \begin{align*} \|S - S_N\|_\infty &\le S(0)\,e^{|r-\sigma^2/2|} \exp(\sigma \|B_N\|_\infty)\sigma \|B-B_N\|_\infty\exp(\sigma \|B-B_N\|_\infty) \\ &\le S(0) e^{|r-\sigma^2/2|} \sigma \exp(3\sigma \|B\|_\infty) \|B-B_N\|_\infty, \end{align*} $$
$$ \begin{align*} \|S - S_N\|_\infty &\le S(0)\,e^{|r-\sigma^2/2|} \exp(\sigma \|B_N\|_\infty)\sigma \|B-B_N\|_\infty\exp(\sigma \|B-B_N\|_\infty) \\ &\le S(0) e^{|r-\sigma^2/2|} \sigma \exp(3\sigma \|B\|_\infty) \|B-B_N\|_\infty, \end{align*} $$
where we used
![]() $\|B-B_N\|_\infty \le \|B\|_\infty + \|B_N\|_\infty \le 2\|B\|_\infty $
. By the Cauchy–Schwarz inequality,
$\|B-B_N\|_\infty \le \|B\|_\infty + \|B_N\|_\infty \le 2\|B\|_\infty $
. By the Cauchy–Schwarz inequality,
It is well known that
![]() $\mathbb {E} [\exp (\alpha \|B\|_\infty )] < \infty $
for every
$\mathbb {E} [\exp (\alpha \|B\|_\infty )] < \infty $
for every
![]() $\alpha> 0$
. Hence, the result now follows from the second bound of Theorem 1.1.
$\alpha> 0$
. Hence, the result now follows from the second bound of Theorem 1.1.
5 Application to option pricing
Now we consider a continuous version of a path-dependent call option with strike price K in a Black–Scholes model with risk-free interest rate
![]() $r>0$
and constant volatility
$r>0$
and constant volatility
![]() $\sigma>0$
. Recall that the asset price
$\sigma>0$
. Recall that the asset price
![]() $S(t)$
at time t is given explicitly by (1.5). The discounted payoff for the case of a continuous arithmetic Asian option with terminal time
$S(t)$
at time t is given explicitly by (1.5). The discounted payoff for the case of a continuous arithmetic Asian option with terminal time
![]() $T=1$
is therefore
$T=1$
is therefore
 $$ \begin{align} P :&= e^{-rT}\max\bigg(\frac 1 T \int_0^T S(t) \,d t -K,0\bigg) \nonumber\\ &= e^{-r}\max\bigg( S(0)\int_0^1 \exp\bigg(\bigg(r-\frac{\sigma^2}{2}\bigg) t+\sigma B(t) \bigg)\,d t - K, 0 \bigg). \end{align} $$
$$ \begin{align} P :&= e^{-rT}\max\bigg(\frac 1 T \int_0^T S(t) \,d t -K,0\bigg) \nonumber\\ &= e^{-r}\max\bigg( S(0)\int_0^1 \exp\bigg(\bigg(r-\frac{\sigma^2}{2}\bigg) t+\sigma B(t) \bigg)\,d t - K, 0 \bigg). \end{align} $$
The pricing problem is then to compute the expected value
![]() $\mathbb {E}(P)$
.
$\mathbb {E}(P)$
.
We use the Lévy–Ciesielski expansion (2.2) and (2.3) for
![]() $B(t)$
and
$B(t)$
and
![]() $B_N(t)$
, and define
$B_N(t)$
, and define
 $$ \begin{align} P_N := e^{-r}\max\bigg( S(0)\int_0^1 \exp\bigg(\bigg(r-\frac{\sigma^2}{2}\bigg) t+\sigma B_N(t) \bigg)\,d t - K, 0 \bigg). \end{align} $$
$$ \begin{align} P_N := e^{-r}\max\bigg( S(0)\int_0^1 \exp\bigg(\bigg(r-\frac{\sigma^2}{2}\bigg) t+\sigma B_N(t) \bigg)\,d t - K, 0 \bigg). \end{align} $$
We are interested in estimating how fast
![]() $\mathbb {E} [|P - P_N|]$
converges to
$\mathbb {E} [|P - P_N|]$
converges to
![]() $0$
as
$0$
as
![]() $N\to \infty $
.
$N\to \infty $
.
Corollary 5.1. For P and
![]() $P_N$
defined by (5.1) and (5.2),
$P_N$
defined by (5.1) and (5.2),
 $$ \begin{align*} \mathbb{E} [|P - P_N|] =\mathcal{O}\bigg(\sqrt{\frac{\ln d}{d}}\bigg), \end{align*} $$
$$ \begin{align*} \mathbb{E} [|P - P_N|] =\mathcal{O}\bigg(\sqrt{\frac{\ln d}{d}}\bigg), \end{align*} $$
where
![]() $d=2^N$
and the implied constant is independent of d.
$d=2^N$
and the implied constant is independent of d.
Proof. It can be easily verified that
Thus,
 $$ \begin{align*} |P- P_N| &\le \bigg| e^{-r} S(0)\int_0^1 e^{(r-\sigma^2/2)t} (\exp(\sigma B(t)) -\exp(\sigma B_N(t))) \,d t \bigg| \\&\le e^{-r} S(0) e^{|r-\sigma^2/2|} \int_0^1 |{\exp}(\sigma B(t)) -\exp(\sigma B_N(t))| \,d t \\&\le e^{-r} S(0)\,e^{|r-\sigma^2/2|} \|{\exp}(\sigma B) - \exp(\sigma B_N)\|_\infty, \end{align*} $$
$$ \begin{align*} |P- P_N| &\le \bigg| e^{-r} S(0)\int_0^1 e^{(r-\sigma^2/2)t} (\exp(\sigma B(t)) -\exp(\sigma B_N(t))) \,d t \bigg| \\&\le e^{-r} S(0) e^{|r-\sigma^2/2|} \int_0^1 |{\exp}(\sigma B(t)) -\exp(\sigma B_N(t))| \,d t \\&\le e^{-r} S(0)\,e^{|r-\sigma^2/2|} \|{\exp}(\sigma B) - \exp(\sigma B_N)\|_\infty, \end{align*} $$
where the last upper bound differs from the upper bound (4.1) on
![]() $\|S-S_N\|_\infty $
only by a factor of
$\|S-S_N\|_\infty $
only by a factor of
![]() $e^{-r}$
. Hence, the result follows from Corollary 1.2.
$e^{-r}$
. Hence, the result follows from Corollary 1.2.
Acknowledgement
An earlier version of this manuscript was posted on arXiv:1706.00915v1.