This is not about the symbolic manipulation of functions so popular these days. Rather it is about the more abstract, but infinitely less practical, problem of the primitive. Simply stated:

Given a derivative f: ℝ → ℝ, how can we recover its primitive?

The roots of this problem go back to the beginnings of calculus and it is even sometimes called “Newton's problem”. Historically, it has played a major role in the development of the theory of the integral. For example, it was Lebesgue's primary motivation behind his theory of measure and integration. Indeed, the Lebesgue integral solves the primitive problem for the important special case when f(x) is bounded. Yet, as Lebesgue noted with apparent regret, there are very simple derivatives (e.g., the derivative of F(0) = 0, F(x)= x2 sin(1/x2)for x ≠ 0) which cannot be inverted using his integral.

The general problem of the primitive was finally solved in 1912 by A. Denjoy. But his integration process was more complicated than that of Lebesgue. Denjoy's basic idea was to first calculate the definite integral 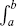f(x) dx over as many intervals (a,b) as possible, using Lebesgue integration. Then, he showed that by using these results, the definite integral could be found over even more intervals, either by using the standard improper integral technique of Cauchy, or an extension technique developed by Lebesgue (see appendix for details).