Article contents
Models of Second-Order Zermelo Set Theory
Published online by Cambridge University Press: 15 January 2014
Extract
In [12], Ernst Zermelo described a succession of models for the axioms of set theory as initial segments of a cumulative hierarchy of levels UαVα. The recursive definition of the Vα's is:
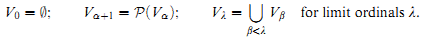
Thus, a little reflection on the axioms of Zermelo-Fraenkel set theory (ZF) shows that Vω, the first transfinite level of the hierarchy, is a model of all the axioms of ZF with the exception of the axiom of infinity. And, in general, one finds that if κ is a strongly inaccessible ordinal, then Vκ is a model of all of the axioms of ZF. (For all these models, we take ∈ to be the standard element-set relation restricted to the members of the domain.) Doubtless, when cast as a first-order theory, ZF does not characterize the structures 〈Vκ,∈∩(Vκ×Vκ)〉 for κ a strongly inaccessible ordinal, by the Löwenheim-Skolem theorem. Still, one of the main achievements of [12] consisted in establishing that a characterization of these models can be attained when one ventures into second-order logic. For let second-order ZF be, as usual, the theory that results from ZF when the axiom schema of replacement is replaced by its second-order universal closure. Then, it is a remarkable result due to Zermelo that second-order ZF can only be satisfied in models of the form 〈Vκ,∈∩(Vκ×Vκ)〉 for κ a strongly inaccessible ordinal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999
References
REFERENCES
- 17
- Cited by


