Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-20T02:34:40.823Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE ELEMENT APPROXIMATION OF A TIME-FRACTIONAL DIFFUSION PROBLEM FOR A DOMAIN WITH A RE-ENTRANT CORNER

Part of: Miscellaneous topics - Partial differential equations Other special functions Partial differential equations, boundary value problems

Published online by Cambridge University Press:  05 April 2017

KIM NGAN LE Open the ORCID record for KIM NGAN LE [Opens in a new window] ,
WILLIAM MCLEAN Open the ORCID record for WILLIAM MCLEAN [Opens in a new window]  and
BISHNU LAMICHHANE Open the ORCID record for BISHNU LAMICHHANE [Opens in a new window]
KIM NGAN LE
Affiliation:
School of Mathematics and Statistics, The University of New South Wales, Sydney 2052, Australia email n.le-kim@unsw.edu.au, w.mclean@unsw.edu.au
WILLIAM MCLEAN*
Affiliation:
School of Mathematics and Statistics, The University of New South Wales, Sydney 2052, Australia email n.le-kim@unsw.edu.au, w.mclean@unsw.edu.au
BISHNU LAMICHHANE
Affiliation:
School of Mathematics and Physical Sciences, University of Newcastle, Callaghan NSW 2308, Australia email blamichha@gmail.com
*
✉w.mclean@unsw.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An initial-boundary value problem for a time-fractional diffusion equation is discretized in space, using continuous piecewise-linear finite elements on a domain with a re-entrant corner. Known error bounds for the case of a convex domain break down, because the associated Poisson equation is no longer 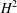$H^{2}$-regular. In particular, the method is no longer second-order accurate if quasi-uniform triangulations are used. We prove that a suitable local mesh refinement about the re-entrant corner restores second-order convergence. In this way, we generalize known results for the classical heat equation.

Keywords

local mesh refinementnon-smooth initial dataLaplace transformation

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 33E12: Mittag-Leffler functions and generalizations 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 65N50: Mesh generation and refinement
Type
Research Article
Information
The ANZIAM Journal , Volume 59 , Issue 1 , July 2017 , pp. 61 - 82
Copyright
© 2017 Australian Mathematical Society 

References

Apel, T., Sändig, A.-M. and Whiteman, J., “Graded mesh refinement and error estimates for finite element solutions of elliptic boundary value problems in non-smooth domains”, Math. Methods Appl. Sci. 19 (1996) 63–85; doi:10.1002/(SICI)1099-1476(19960110)19:1¡63::AID-MMA764¿3.0.CO;2-S.3.0.CO;2-S>CrossRefGoogle Scholar
Bezanson, J., Edelman, A., Karpinski, S. and Shah, V. B., “Julia: a fresh approach to numerical computing”, Technical Report, 2015, arXiv:1411.1607v4.Google Scholar
Chatzipantelidis, P., Lazarov, R. D., Thomée, V. and Wahlbin, L. B., “Parabolic finite element equations in nonconvex polygonal domains”, BIT 46 (2006) S113–S143; doi:10.1007/s10543-006-0087-7.CrossRefGoogle Scholar
Ciarlet, P.  G., The finite element method for elliptic problems (SIAM, Philadelphia, 2002).CrossRefGoogle Scholar
Drazer, G. and Zanette, D., “Experimental evidence of power-law trapping-time distributions in porous media”, Phys. Rev. E (3) 60 (1999) 5858–5864; doi:10.1103/PhysRevE.60.5858.CrossRefGoogle ScholarPubMed
Geuzaine, C. and Remacle, J. F., “Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities”, Int. J. Numer. Methods Engrg. 79 (2009) 1309–1331; doi:10.1002/nme.2579.CrossRefGoogle Scholar
Gia, Q. T. L. and McLean, W., “Numerical solution of a parabolic equation on the sphere using Laplace transforms and radial basis functions”, in: Proceedings of the 15th Biennial Computational Techniques and Applications Conference, CTAC-2010 (eds McLean, W. and Roberts, A. J.), ANZIAM J. 52 (2011) C89–C102; http://journal.austms.org.au/ojs/index.php/ANZIAMJ/article/view/3922.Google Scholar
Grisvard, P., Singularities in boundary value problems (Springer, Berlin, 1992).Google Scholar
Jin, B., Lazarov, R. and Zhou, Z., “Error estimates for a semidiscrete finite element method for fractional order parabolic equations”, SIAM J. Numer. Anal. 51 (2013) 445–466; doi:10.1137/120873984.CrossRefGoogle Scholar
Klafter, J. and Sokolov, I. M., First steps in random walks: from tools to applications (Oxford University Press, Oxford, 2011).CrossRefGoogle Scholar
McLean, W., “Regularity of solutions to a time-fractional diffusion equation”, ANZIAM J. 52 (2010) 123–138; doi:10.1017/S1446181111000617.CrossRefGoogle Scholar
McLean, W. and Thomée, V., “Numerical solution via Laplace transforms of a fractional order evolution equation”, J. Integral Equations Appl. 22 (2010) 57–94; doi:10.1216/JIE-2010-22-1-57.CrossRefGoogle Scholar
Mustapha, K. and McLean, W., “Piecewise-linear, discontinuous Galerkin method for a fractional diffusion equation”, Numer. Algorithms 56 (2011) 159–184; doi:10.1007/s11075-010-9379-8.CrossRefGoogle Scholar
Ross, B., “The development of fractional calculus 1695–1900”, Historia Math. 4 (1977) 75–89; doi:10.1016/0315-0860(77)90039-8.CrossRefGoogle Scholar
Thomée, V., Galerkin finite element methods for parabolic problems (Springer, Berlin, 1997).CrossRefGoogle Scholar
Weideman, J. A. C. and Trefethen, L. N., “Parabolic and hyperbolic contours for computing the Bromwich integral”, Math. Comp. 76 (2007) 1341–1356; doi:10.1090/S0025-5718-07-01945-X.CrossRefGoogle Scholar
Weiss, M., Elsner, M., Kartberg, F. and Nilsson, T., “Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells”, Biophys. J. 87 (2004) 3518–3524; doi:10.1529/biophysj.104.044263.CrossRefGoogle ScholarPubMed