Introduction
In October 1996 an eruption occurred under 500–750m of ice in the Vatnajökull ice cap, Iceland. On the ice surface a north–south-trending ~2–4 km wide and ~6–8 km long depression was formed above the subglacial Gjálp volcano (Fig.1; Reference Einarsson, Brandsdóttir, Gudmundsson, Björnsson, Grönvold and SigmundssonEinarsson and others, 1997; Reference Gudmundsson, Sigmundsson and BjörnssonGudmundsson and others, 1997; Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others, 2001). About 3 km3 of meltwater generated in the eruption drained toward the subglacial lake Grímsvötn (Fig. 1; Reference Gudmundsson, Sigmundsson and BjörnssonGudmundsson and others, 1997). The sudden removal of ice led to an inflow of ice to the elongated depression. In the first year after the eruption, the width of the depression doubled, and the infilling rate gradually diminished by a factor of five. During the first months of this period, the inflow was greatly influenced by subglacial melting (mass removal) due to cooling of the subglacial volcano (Fig.1; M.T. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others, in press).

Fig. 1. (a): Map of the Gjálp eruption area fromJune 1997. The dashed box shows the area covered by the interferograms in Figure 2 and the motion maps in Figure 5. The location is shown on the small map ofVatnajökull ice cap in Iceland. (b, c): Plots of profiles b and c, respectively. The black shading shows the Gjálp volcano formed in the October 1996 eruption. From M.T. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others (in press).
Various complementary observations have been conducted in the Gjálp area since October 1996. Interferograms, generated from repeat-pass synthetic aperture radar (SAR) images from the European Remote-sensing Satellite (ERS-1/-2) tandem mission acquired over a 2 year period after the Gjálp eruption, were used by Reference Rott and SiegelRott and Siegel (1998) and Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others (2001) to study the infilling rate of the depression. The interferometric tandem data reveal information about daily one-dimensional change in range from ground to satellite, with high spatial resolution and few mm accuracy (e.g. Reference Massonnet and Feigl.Massonnet and Feigl, 1998). Differential global positioning system (DGPS) and airborne altimetry soundings have been used to acquire data at the eruption site to construct time sequences of elevation maps, with ~5–20m accuracy (Reference Gudmundsson, Sigmundsson and BjörnssonGudmundsson and others, 1997, Reference Gudmundsson, Högnadóttir, Björnsson, Pálsson and Sigmundsson1999; Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others, 2001). GPS measurements of locations of stakes at the ice surface have also been repeatedly performed to provide point-wise information on horizontal displacements with 5–10% accuracy. Here, we present results of combining interferograms, elevation maps and point-wise information on horizontal displacements into high-resolution three-dimensional (3-D) motion maps of the non-stationary infilling rate (gradually diminishing with time) of the depression during the first year after the eruption. In the area, surface-parallel ice flow (e.g. Reference Joughin, Kwok and FahnestockJoughin and others, 1998; Reference Mohr, Reeh and MadsenMohr and others, 1998) cannot be assumed, and general ice-flow models may be inadequate due to the subglacial melting.
The data are fused by a method suggested by Reference GudmundssonGudmundsson (2000) and S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others (in press), where the problem of finding the 3-D motion field is modelled with Markov random-field regularization and optimized with a simulated annealing algorithm. The optimization process needs to be initialized. Here we use two elevation maps obtained 1year apart to initialize the vertical motion maps. We use interpolation of sparse GPS observations of the horizontal displacements to initialize the horizontal motion maps. The complementary datasets cover different time intervals, and are time-scaled, before optimization, by using a time-dependent non-stationary calibration factor estimated by various internal and external comparisons of the different datasets. Finally, 3-D motion maps are inferred for 1–2 January, 12–13 March, 21–22 May and 8–9 October 1997, and the results used to estimate the cooling rate of the subglacial volcano.
Observations
Four interferograms from the Gjálp area were used for the data fusion (Table 1; Fig. 2), acquired during the ERS-1/-2 tandem mission, from ascending satellite passes. They are a subregion of four interferograms used by Reference Rott and SiegelRott and Siegel (1998) and Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others (2001). Known topographical and orbital errors have been removed by utilizing digital elevation models (DEMs) and knowledge of the orbital trajectories, respectively. Themodulo-2π ambiguity was removed using least-squares unwrapping with iterative error correction (Reference Siegel and SteinSiegel, 1999). Resi-dual orbital errors as well as noise of atmospheric origin are considered to be negligible for the interferograms in Figure 2. Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others (2001) estimated the residual topographical errors to be at most 0.2 fringes (~0.5 cmd–1) by assuming the lowest altitude of ambiguity in Table 1 (43m) and assuming an elevation error of 20m for the DEMs. The altitude ofambiguity is 43–237m for the interferograms (Table 1), and the errors of elevation in the DEMs are generally much smaller than 20m since the accuracy of the DGPS measurements used is 2–3m. Thus, the errors in the interferograms are expected to be smaller than 0.5 cmd–1. For each pixel in the interferograms, the scalar change in range from the satellite to ground can be described by
Table 1. Characteristics of the interferometric observations (Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others, 2001). First column refers to Figure 2

where u is a 3-D displacement vector, –s is a unit vector pointing from the ground towards the satellite and T denotes the transpose of the unit vector (e.g. Reference Massonnet and Feigl.Massonnet and Feigl, 1998). The microwave incidence angle was ~23˚ from vertical and ~15.6˚ south of west in the horizontal plane at the Gjálp area. Using knowledge about the orbital trajectories, elevation and geographical position of the image frames, the unit vector in Equation (1) was calculated as
where N, E and V are north, east and vertical direction, respectively. Hence, the interferograms are composed of 3-D motion fields projected onto the unit vector ŝ, where the highest and lowest contributions are due to the vertical and north displacements, respectively.
DGPS observations of displacements of stakes, within and close to the Gjálp area, were conducted at 11 points (location of stakes) in summer 1997, and at 16–26 points in the summers of 1998–2000. They provide information about the two-dimensional horizontal displacement rates at sparse locations. The displacements were 4–6m over the measurement interval, with an accuracy cautiously estimated as 1m; yielding a relative accuracy of 20%. Of available sparse GPS observations of stakes, we use 9, 24, 4 and 2 points in 1997, 1998, 1999 and 2000, respectively, composed into one dataset (Fig. 3a) by applying the time-scaling given in Figure 4. The error in the GPS data is random, and the error of the mean in the calibration should be in proportion to n–1/2, where n is the number of stakes used (e.g. Reference ChatfieldChatfield, 1983). Thus, we estimate the accuracy of the calibration as varying from 5% (largest number of stakes) to 15%( smallest number of stakes).

Fig. 3. Observations used for initialization of vertical and horizontal motion maps (the frames are the same as in Figure 2, except reaching 2 km further to the north). (a, b) DEMs from 10 June, 1997 and 1998, respectively, used for initialization of vertical motion maps. Locations of DGPS observations used for the construction of the two DEMs are marked with + in (b). Line1in (a) marks the boundaries of the mask used in Figure 5; line 2 in (b) encloses the central parts (Fig. 4) of the depression (roughly estimated). Imprinted vectors in (a), labelled with red dots, show GPS-measured horizontal displacement rates observed in the summers of 1997–2000, where all results have been scaled to fit the elapsed time interval of 1 May–25 August 1998. Vectors labelled with green dots are predicted by interpolating the observations and by assuming smoothly varying flow field, parallel to flowlines. The east flow field is expected to be close to zero at points labelled with blue dots, as they are located at ice divides and the regional flow is directed approximately toward south-southeast.

Fig. 4. Time calibration of non-stationary displacement rates in the Gjálp area. The displacement rates have been scaled with the average vertical displacement between June 1997 and 1998, as estimated from elevation maps. (a) Estimated calibration with time of horizontal displacements, and vertical displacements at places where the basal melting is expected to have small influence (outside the central parts of the depression, Fig. 3b). (b) Estimated calibration with time of vertical displacements in the central parts of the depression. The bar-widths are equal to the elapsed time intervals used for each of the various observations.
A time sequence of DEMs with 100 6100 m grid spacing has been compiled for January 1997 (observed by airborne altimetry) and June 1997, 1998 and 1999 (observed by DGPS), by using an interpolation of observations of the ice surface elevation along survey lines, together with knowledge of the depression patterns. The accuracy of the DEMs is considered better than ~5mor~20m, when using DGPS or airborne altimetry, respectively. Here, the vertical motions were observed as the difference between two accurate DEMs, acquired in June 1997 and 1998 (Fig. 3). According to the two DEMs, the uplift from June 1997 to 1998 was ~30–35m at the central parts of the depression. Although the depression is located 200–300m above the regional equilibrium line (Reference Björnsson, Pálsson, Gðmundsson and HaraldssonBjörnsson and others, 1998), the annual net balance of the inner part of the depression is considered close to zero, as melting was locally enhanced by the dark tephra. This is supported by the absence of snow cover within the depression in late summer of 1997 and 1998.
Both interferometric SAR (InSAR) and GPS observations indicate a stable flow field at the nearest surrounding areas not affected by the depression, with a regional flow directed toward south-southeast (Fig. 3a). Previous interferometric studies of the flow field in the Gjálp area indicate small-scale instabilities and irregular changes of the non-stationary motion field in January 1997, but after February 1997 the non-stationary ice flow gradually and regularly diminished with time (Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others, 2001). Furthermore, the subglacial melting was greatly reduced from January to October 1997. The different datasets from the Gjálp area cover different time intervals from January 1997 to September 2000, and need to be made time-consistent before combination. Here, we use time-variant (gradually diminishing) calibration of the non-stationary parts of the flow field (Fig. 4), estimated by internal and external comparison of the different datasets and by assuming regular changes in the 3-D flow field. Abrupt changes in the surface slope were observed in January and partly in June 1997, approximately at the boundary marked with line 2 in Figure 3b. This indicates a spatial variation in the basal melting, with highest values at the central parts enclosed by line 2. Vertical motions were extracted from a synthesis of the InSAR and DEM datasets along a transect that was both perpendicular to the radar beam and approximately parallel to the net horizontal flow towards the centre of the cauldron. This synthesis of the data indicates that the spatial variation in the basal melting can be accounted for by using two calibration factors for the vertical motions, one within and one outside the central parts of the depression (Fig. 4).
3-D Motion Maps
According to Equations (1) and (2), the interferograms in Figure 2 record ![]() where k is a pixel number, and VNk, VEk and VVk, are the north, east and vertical components of deformation, respectively. Here, the task is to construct the three motion maps VN, VE and VV, by combining the known interferogram Δρr and the information about the 3-D motion field from the ground observations. This 3-D problem can be separated into two two-dimensional problems (Reference GudmundssonGudmundsson, 2000; S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others, in press), written as
where k is a pixel number, and VNk, VEk and VVk, are the north, east and vertical components of deformation, respectively. Here, the task is to construct the three motion maps VN, VE and VV, by combining the known interferogram Δρr and the information about the 3-D motion field from the ground observations. This 3-D problem can be separated into two two-dimensional problems (Reference GudmundssonGudmundsson, 2000; S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others, in press), written as
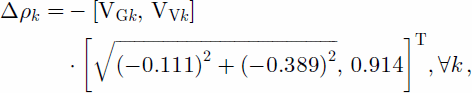
and

where VGk is the deformation in the ground range direction of the SAR (Fig. 2a). Here, we use Dr when constructing VG and VV in Equation (3), and the resulting VG when constructing VN and VE in Equation (4). A general form of Equations (3) and (4) is written
where y1k is known for all pixels k, x1k and x2k are known from ground observations at sparse pixels, and u1 and u2 are constants.
Optimization
An optimization method that uses Markov random field (MRF) regularization and simulating annealing algorithm (Reference GudmundssonGudmundsson, 2000; S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others, in press) was used to construct 3-D motions maps at the Gjálp area for 1–2 January, 12–13 March, 21–22 May and 8–9 October 1997 (Fig. 5). The optimization was done separately for each of the 4 days, by combining a corresponding interferogram (Fig. 2) and ground observations. The optimization process was initialized with 3-D motion maps of the same geometry and resolution as the interferograms. First, interpolations of time-scaled ground observations were used to infer initial 3-D motion maps for 8–9 October 1997, corresponding to the interferogram in Figure 2d. The initial vertical motion map was inferred from the two compiled DEMs in Figure 3. The regional flow trend was toward the south in the Gjálp area. Hence, the east component of the flow field can be assumed to be close to zero at the ice divides (blue points in Fig. 3a). The same cannot be assumed for the north component of the motion field. This is supported by the GPS observation of stakes in the summers of 1997– 2000. Here we initialized the east motion map by using a cubic spline of the observed and predicted values at the red, green and blue points (Fig. 3a), and the north motion map by a cubic spline of the values at red and green points. Initial VG was calculated by using Equation (4) and the initial east and north motion maps.

Fig. 5. Optimized vertical (VV ; positive upward), east (VE ; positive to the east) and north (VN; positive to the north) motion maps, for 1–2 January, 12–13 March, 21–22 May and 8–9 October 1997 (the days of the interferometric observations in Fig. 2). Note the differences in scale, i.e. change in deformation rates with time.
After an optimization of 3-D motion maps for 8–9 October 1997, the results were time-scaled (Fig. 4), and used as initial values for an optimization of 3-D motion maps for 21–22 May 1997. This chain process was then repeated for 12–13 March 1997 by using scaling of optimized 3-D motion maps for 21–22 May, and for 1–2 January 1997 by using scaling of optimized 3-D motionmaps for 12–13 March. In this way, the assumption of having regular ice flow with time at the depression has been used to reduce errors due to differences in times of observations between the interferometric and ground observations. Of available interferometric observations, the October interferogram in Figure 2d is closest in time to the ground observations in Figure 3, and is used in the first optimization of the previously described chain process.
In MRF regularization, an optimal image is interpreted as a realization of a randomvariable, where the value of each pixel in the image grid is only dependent on its nearest neighbours (e.g. Reference Li and KumiiLi, 2001). This provides a convenient way of modeling image texture and spatial correlation of image pixels. The MRF model used to regularize the data fusion is based on energy functions that take its minimum values for optimal motion maps of x1 and x2 in Equation (5). Here, we only describe the energy functions briefly, but detailed explanation of the optimization process is given by S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others (in press). The constraints in the MRF regularization are as follows:
(1) The relationship to the known image y in Equation (5) is implemented as
where n is a pixel number and γ1 =10.
(2) The relationship to the sparse ground observations in Figure 3 is implemented as

and
where xK1 and xK2 are initial interpolated motion maps and γ2 = γ3 =5.w1 andw2 are uncertainty images that take the value 1 at pixels corresponding to the sparse locations of ground observations (Fig. 3) and decay rapidly to zero with distance from them (Reference GudmundssonGudmundsson, 2000; S. Gudmundsson and others, in press).
(3) The assumption of a smoothly varying flow field is implemented as a penalization of the first derivative with the approximation
and

where i; j are the row and column numbers, respectively (a pixel number ![]() where ni is the row width of the motion maps), γ4 =1 and γ5 = 2. The constraints in Equations (6–10) are utilized when optimizing both the motion maps in Equations (3) and (4).
where ni is the row width of the motion maps), γ4 =1 and γ5 = 2. The constraints in Equations (6–10) are utilized when optimizing both the motion maps in Equations (3) and (4).
(4) An additional constraint is only used when x1 = VN and x2 = VE in Equation (5). It utilizes a tendency of the horizontal displacement to be directed parallel to the flowlines at the surface, implemented as

where z is an elevation map of the surface in the same geometry and resolution as the motion maps and γ6 = 20.
Constraints 1–3 are the same as those used by Reference GudmundssonGudmundsson (2000) and S. Reference Gudmundsson, Sigmundsson and CarstensenGudmundsson and others (in press). U6 was added to the MRF regularization for the purpose of inferring the 3-D motion field in the Gjálp area. Because the energy functions in Equations (6–11) represent different types of quantities, the ratios of the γ coefficients do not represent the relative weighting of each term in the optimization. The γ coefficients used for U1, U4 and U5 are the same as those determined by S. Gudmundsson and others (in press). In that case, the sparse ground observations of the vertical, east and north components were all made at the same locations, and over a time interval close to the time intervals covered by the interferograms. This is not the case here, so we take γ2 = γ3 = 5 in Equations (7) and (8), which is only half the value recommended by S. Gudmundsson and others (in press). This deliberately weakens U2 and U3. The vertical motion map is mainly determined by U1, since the interferograms are most sensitive to vertical motion. U6 is given a relatively large weight since it determines the horizontal flow field.
Estimation of errors
To estimate errors of the 3-D motion maps in Figure 5, we use the errors of the observations and an assumption of a smooth time and spatially varying motion field. This assumption is supported by the observations. Motions that were unaffected by the depression are not inferred at 1–2 January, 12–13 March and 21–22 May 1997, and are therefore masked out in Figure 5. Furthermore, highly decorrelated areas are masked out in the 8–9 October 1997 motion maps. Ground observations suggest that the south-southeast-trending regional flow has only a small influence on the net motions at the depression (Fig. 3). Its influence is greatest on the north component of the motion field in the northernmost region of the depression. This regional flow is not expected to be detected in the interferograms, since it is almost perpendicular to the ground range of the SAR (Fig. 2a). Here, the regional flow is assumed to have a negligible influence on the inflow of ice into the depression, and hence is not considered in the data fusion.
The optimization process was initialized by 3-D motion maps for 8–9 October 1997, created from interpolated and time-scaled ground observations. The initial vertical motion map was estimated by using a time-scaled (Fig. 4) difference of the two DEMs compiled for June 1997 and 1998 (Fig.3). The time-scaling was estimated by various comparisons of the observations. The comparisons indicated a high consistency in the complementary observations, and therefore accurately estimated time calibration. Using the uncertainties of the DEMs, the error of the difference is found to be at most 7 ma–1 (2 cmd–1 on average). Due to the smooth variation of the motion field and the overdetermined error of 7 ma–1, we assume the error of the initial vertical motion map for 8–9 October to be ~2 cmd–1 (~25–50%of the observed motions). Initial east and north motion maps were created by using interpolation of GPS observations of location of stakes and by assuming smoothly varying flow field parallel to flowlines. Due to the large number of stakes and the knowledge of the motion field, we cautiously estimate the error as double the error in the observations, or 10–20%.
The uncertainty of the 3-D motion maps is expected to be reduced after the optimization of Equations (6–11). To estimate the possible reductions of errors by an optimization of Equations (6–10), S. Gudmundsson and others (in press) used a 1646164 pixel error-free synthetic interferogram with the vertical, east and north motion components known for all pixels. The synthetic interferogram was created by using a mass-balance equation to describe the surface ice flow at the Gjálp depression (Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others, 2001). Here, the same synthetic interferogram was used to estimate possible reductions of errors by an optimization of Equations (6–11). This was done by assuming sparse ground observations within the synthetic interferometric area, with spatial distribution similar to those in Figure 3 (the real observations). A cubic spline was used to initialize the 3-D motion maps. After optimization, we found the errors to be reduced by 50%, 28% and 20% in the vertical, east and north motion maps, respectively. Inclusion of the horizontal flow-field constraint in Equation (11) proved important since it increased the reduction of errors in the east motion map from 16% to 28% and in the north motion map from 10% to 20%. No errors were assumed for the observations in the test case. However, the errors of the optimized vertical, east and north motion maps for 8–9 October 1997 (Fig. 5) are assumed to be at most ~25% (0.50650%), ~14% (0.72620%) and ~16% (0.80620%), respectively. This can be justified since the error in the interferometric observations is small, and almost negligible compared to other errors. Large errors in ground observations increase the errors in the initial 3-D motion maps. Due to the relationship of the 3-D motion maps to interferometric observations in Equation (6), the ratio of optimized to initial errors of the 3-D motion maps decreases with increased initial errors.
The optimized 3-D motion maps for 8–9 October 1997 were time-scaled (Fig. 4), and used as initial values for an optimization of 3-D motion maps for 21–22 May 1997. This chain process was then repeated for 12–13 March and 1–2 January 1997, as previously described. Due to the accurate time calibration, low error in the interferograms and cautiously estimated errors of the optimized 3-D motion maps for 8–9 October 1997, we assume the errors of all the 3-D motion maps in Figure 5 to be close to those estimated for 8–9 October 1997.
Results
Figure 5 shows the inferred spatial variation of the motion field, and changes of ice inflow rates and surface uplifting from January to October 1997. The inferred flow fields from January and October 1997 are shown as vectors superimposed on ice surface contours in Figure 6. The 3-D motion maps provide a consistent view of the ice inflow toward the depression (Fig. 5), which cannot be obtained by independent interpretation of the input datasets. The 3-D motion maps show inflow of ice towards the central part of the elongated depression (Fig. 6), which gradually diminished from January to October 1997 (Fig. 5). Furthermore, during this period the vertical motion maps show uplift in the central part of the depression, which decreased over time (Fig. 5). Over the 4 days covered by the 3-D motion maps, the ratio of uplift to ice flow into the depression was lowest on 1–2 January and highest on 8–9 October (Fig. 5). This is a consequence of reduced basal melting with time, due to gradual cooling of the subglacial volcano.

Fig. 6. Vector plot of the inferred 3-D motion fields imprinted on elevation maps of the Gjálp eruption area (see the location of the frames in Fig. 1a). Vertical and horizontal displacements are displayed as blue and red vectors, respectively. The same color bar applies to both the elevation maps, and appropriate reference vector amplitudes are shown above the frames.
The cooling rate was estimated from the optimized 3-D motion maps (Fig. 7). The mass-continuity equation (e.g. Reference PatersonPaterson, 1994, p. 334) applied to the depression gives

Fig. 7. Estimated power supplied to melt the ice above the cooling Gjálp volcano (left y axis), and the corresponding water-equivalent units (right y axis). Previous estimations of the melt rate are also plotted for comparison (Reference Gudmundsson, Högnadóttir, Björnsson, Pálsson and SigmundssonGudmundsson and others, 1999).
where the ice volume S = hA, A is a surface area, h is the ice thickness, bs is the surface mass-balance rate, bb is the subglacial melting rate and Q is the ice flux. On a rectangular grid, Equation (12) can be expressed as

where Δh/Δt is the rate of change in elevation (Δh/Δt = VV, where VV is the inferred vertical motion map and Δt = 1 day), VE and VN are the east and north motion maps (surface velocities), respectively, and ΔE = ΔN = 20 m is the grid spacing in east and north direction, respectively. The DEMs and a map of the bedrock topography with an accuracy of 20m (M.T. Gudmundsson and others, in press) were used to estimate the ice thickness h. As mentioned earlier, bs can be assumed to be zero. Here we assume the average horizontal velocity over the ice thickness to be 90% of the surface velocity (Reference NyeNye, 1965). Thus, bs is the only unknown parameter in Equation (13) and can be calculated by using the inferred 3-D motion maps and the estimated ice thickness. The values in Figure 7 were estimated by calculating the basal melt rate in Equation (13) only within the area affected by the depression (approximately bounded by the ice divides). The uncertainties (~30%) were calculated by using Equation (13), the estimated errors of the inferred 3-D motion maps (Fig. 5) and the error of the observed ice thickness (h). We found the error in the subglacial melt rate to be mainly caused by the error in the vertical motion maps.
All meltwater from the Gjálp area drained toward the nearby subglacial lake Grímsvötn (Fig. 1). Reference Gudmundsson, Högnadóttir, Björnsson, Pálsson and SigmundssonGudmundsson and others (1999) estimated the power of melting above the cooling Gjálp volcano as 10 GW 4months after the start of the eruption on 30 September 1996, and 2–4 GW 1year after the eruption. Our estimates of the melt rate above the cooling Gjálp volcano are in good agreement with previous estimates (Fig.7), but provide denser, more accurate results for the meltrate pattern.
A simplified ice-flow model was used by Reference Björnsson, Rott, Guðmundsson, Fischer, Siegel and GuðmundssonBjörnsson and others (2001) to simulate ice flow along a profile in the Gjálp depression. The model results confirmed the general-ice flow patterns for 12–13 March, 22–23 May and 8–9 October, but failed to describe the ice flow for 1–2 January. Themodel did not describe the spatial pattern of the ice flow and the influence of the basal melting. Our results show the same general pattern of gradually diminishing ice flow into the depression, but provide a much improved picture of the 3-D motion field, with respect both to basal melting and to irregularities in the surface elevation.
Conclusion
An optimization process that uses MRF regularization and simulated annealing optimization has been used to combine interferometric and other ground displacement data to infer time sequences of high-resolution 3-D motion maps, describing the ice-flow rates during the infilling of the surface depression formed in the October 1996 eruption in Vatnajökull. These synthesized motion maps provide a consistent view of the 3-D motion field, both spatially and with time, which cannot be seen by separate interpretation of the input datasets. According to the inferred datasets, the net basal melting due to the cooling Gjálp volcano was ~55m3 s–1 at 1–2 January 1997, gradually diminishing to ~5m3 s–1 at 8–9 October 1997. Our results are in good agreement with previous estimations of water drainage from the Gjálp area, but provide denser, more accurate results for the melt-rate pattern.
Acknowledgements
The work was supported by the Research Fund of the University of Iceland. Parts of the fieldwork were done by volunteers of the Iceland Glaciological Society. We are indebted to A. Siegel and A. Fischer for preparing and supplying interferometric data, F. Pálsson for assistance with finding and preparing data and Th. Högnadóttir for working on DEMs. We thank G. Flowers for useful discussions of the evaluation of the subglacial melting rate.











