1. Introduction
In recent decades, significant air and ocean warming has been observed in Greenland (e.g. Reference Meehl and SolomonMeehl and others, 2007; Reference Levitus, Antonov, Boyer, Locarnini, Garcia and MishonovLevitus and others, 2009), causing mass loss to accelerate on the ice sheet by surface melting, runoff and ice discharge (e.g. Reference Van den BroekeVan den Broeke and others, 2009; Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011). The current Greenland ice sheet mass loss is estimated to range from 191 ±23 to 240±28Gta–1 by combining NASA’s Ice, Cloud and land Elevation Satellite (ICESat) elevation measurements, firn compaction and modeled surface density (Reference SørensenSørensen and others, 2011). The Gravity Recovery and Climate Experiment (GRACE) mission provided an independent check that confirmed the Greenland ice sheet loss of 219 ±38 Gta–1 for 2002-09 (Reference Chen, Johannessen, Wang and OhmuraJ.L. Chen and others, 2011). In the last decade, about half of the mass loss is due to ice dynamics, and the rest is due to surface mass-balance processes (Reference Van den BroekeVan den Broeke and others, 2009). Surface mass balance for the Greenland ice sheet can be approximated by snowfall (accumulation) minus ablation, and its interannual variability over the 1957-2008 period is very large, with a standard deviation, a, of 107 Gta–1 (Reference EttemaEttema and others, 2009).
Accumulation is the only mass input to the Greenland ice sheet, and its magnitude, spatial and temporal distributions are poorly constrained, especially in the southeast sector (e.g. Reference BurgessBurgess and others, 2010). Measurement uncertainty of the accumulation input to the ice sheet leads to uncertainty in the total mass budget of Greenland. The mass budget needs to be estimated in order to understand ice-sheet behavior, which is a critical question. Since accumulation may increase with future warming (e.g. Reference Meehl and SolomonMeehl and others, 2007), reducing uncertainty in ice-sheet accumulation and better estimating the total mass budget is also critical. Recently, for the 2007-09 time period, the southeast sector of the ice sheet has lost 172 ±44Gta–1, which is a large part of the total mass loss over the whole ice sheet (Reference Chen, Johannessen, Wang and OhmuraJ.L. Chen and others, 2011). However, an increase in accumulation rates that could offset this mass loss has not yet been observed.
We present snow accumulation rates derived from new firn cores and ground-penetrating radar (GPR) measurements across poorly sampled areas of the southeastern Greenland ice sheet. The objectives of this study are to confirm the modeled high snow accumulation rates and to quantify the spatial and temporal variations in snow accumulation over the past 30 years. Below we introduce previous work on Greenland accumulation estimates and on GPR studies, which serve as the context for our study.
1.1. Accumulation-rate measurements
Accumulation rates over the Greenland ice sheet have been studied using a variety of methods. We discuss three of these, and highlight the need for additional in situ measurements in the southeast sector of the ice sheet. In the first method, accumulation maps are generated by interpolating in situ point measurements. Ice cores and snow pits, located in the upper accumulation area, are the most common observations. Along the coast of Greenland, the Danish Meteorological Institute maintains meteorological stations to measure accumulation from solid precipitation minus evaporation. Reference BensonBenson (1962) and Reference Ohmura and ReehOhmura and Reeh (1991) produced initial snow accumulation maps from these limited observations. Since then the spatial and temporal resolution of these accumulation maps has been increased using updated ice-core data, an increasing number of coastal weather stations, and more sophisticated interpolation techniques (Reference Ohmura, Calanca, Wild and AnklinOhmura and others, 1999; Reference Calanca, Gilgen, Ekholm and OhmuraCalanca and others, 2000; Reference Bales, McConnell, Mosley-Thompson and CsathoBales and others 2001, Reference Bales2009; Reference McConnellMcConnell and others, 2001; Reference CogleyCogley, 2004). In the second method, regional climate models are used to simulate recent climate (typically since 1958 because of the availability of reliable reanalysis fields) of the ice sheet and also provide accumulation maps (Reference FettweisFettweis, 2007; Reference Hines and BromwichHines and Bromwich, 2008; Reference Ettema, Van den Broeke, Van Meijgaard, Van de Berg, Box and SteffenEttema and others, 2010; Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdottir, Mottram and SimonsenLucas-Picher and others, 2012). However, all the different modeled snow accumulation outputs do not fully agree, and the lack of in situ measurements in the southeast sector does not yet allow model comparison and validation (Reference RaeRae and others, 2012). For example, the Regional Atmospheric Climate Model (RAC-MO2; Reference EttemaEttema and others, 2009) modeled higher accumulation in southeast Greenland compared to estimates from Reference BoxBox and others (2006) using the Fifth Generation Mesoscale Model modified for polar climates (Polar MM5), or to Reference FettweisFettweis (2007) using the Modele Atmospherique Regional (MAR). A hybrid technique uses the discrepancies between regional climate model outputs and in situ measurements to generate correction factors to produce calibrated accumulation maps (Reference BoxBox and others, 2006; Reference BurgessBurgess and others, 2010). In the third method, accumulation maps are reconstructed using meteorological reanalysis, including ERA-40 (e.g. Reference Hanna, McConnell, Das, Cappelen and StevensHanna and others, 2006), 20CR (e.g. Reference HannaHanna and others, 2011) and ERA-Interim (e.g. L. Reference Chen, Johannessen, Wang and OhmuraChen and others, 2011).
The southeast sector of the ice sheet represents only 14% of the total ice-sheet area and accounts for 3 1 % of total accumulated mass and 32% of annual accumulation variability (Reference BurgessBurgess and others, 2010). Only 2% of the available firn-core data of the Greenland ice sheet are found in the southeast sector, but no firn-core data are found below 2000 m elevation, where higher accumulation rates are predicted: >2mw.e. a- 1 (Reference BurgessBurgess and others, 2010) and reaching up to 5mw.e. a- 1 (Reference RaeRae and others, 2012). It is difficult to estimate accumulation close to the southeast Greenland coast, where orographic precipitation dominates and topography is complex (e.g. Reference BurgessBurgess and others, 2010; Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdottir, Mottram and SimonsenLucas-Picher and others, 2012). These studies emphasized the need for in situ measurements to constrain climate models in this sector. In addition, Reference HannaHanna and others (2011) noted the lack of validation data for climate models and showed that uncertainties in southeast Greenland accumulation are greatest where accumulation rates are highest, and where both accumulation and topographic gradients are significant.
1.2. Ground-penetrating radar (GPR)
GPR allows us to capture spatial variability in accumulation over distances of tens to hundreds of km. Small-scale spatial variability in accumulation (∼5-10 km), mostly due to snow redistribution and surface undulations, is not captured in point measurements from cores and is not taken into account in regional climate models with large gridcells (∼5-25 km). The spatial variability of snow accumulation can be observed in GPR transects that show continuous internal reflection horizons (IRHs) (e.g. Reference Arcone, Spikes, Hamilton and MayewskiArcone and others, 2004, Reference Arcone, Spikes and Hamilton2005a; Reference Dunse, Eisen, Helm, Rack, Steinhage and ParryDunse and others 2008). IRHs at relatively shallow depths (<50 m) are primarily due to density contrasts (e.g. Reference Eisen, Wilhelms, Nixdorf and MillerEisen and others, 2003; Reference Arcone, Spikes and HamiltonArcone and others, 2005a). The isochronous nature of IRHs has been confirmed using the depth-age scale from firn cores located at both ends of the GPR profile (Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004; Reference Eisen, Wilhelms, Steinhage and SchwanderEisen and others, 2006).
In the southeast sector of the ice sheet, for an elevation range between ∼1840 and ∼2350 m, two major snow facies are found in our GPR profile. At elevations above 2000 m, the dry-snow facies is represented with no or little melt (∼ 1-3 cm melt layers). At lower elevation, the percolation facies is found where surface snow melts and travels downward through the snowpack until it refreezes (e.g. Reference BensonBenson, 1962), which likely produces vertical ice pipes and horizontal ice layers. Recent GPR studies in West Greenland documented the presence of ice layers within the firn (e.g. Reference ParryParry and others, 2007; Reference Dunse, Eisen, Helm, Rack, Steinhage and ParryDunse and others 2008; Reference Brown, Harper, Pfeffer, Humphrey and BradfordBrown and others, 2011). These features complicate tracing of continuous IRHs in the firn depending upon melt intensity, spatial scale and radar frequency. Reference Dunse, Eisen, Helm, Rack, Steinhage and ParryDunse and others (2008), using GPRs with frequency of 500 and 800 MHz, were able to track IRHs down to 10 m depth. Reference Brown, Harper, Pfeffer, Humphrey and BradfordBrown and others (2011) found no correlation between IRHs and firn stratigraphy in the higher-elevation part of the percolation zone in West Greenland and assumed the IRHs were multi-annual features (2-10 years) in the lower part of the percolation zone. These studies highlight the challenges in identifying isochronous IRHs from GPR profiles, and tracking them over many kilometers. However, all of these studies were conducted in regions where accumulation rates are low compared to southeast Greenland. In the southeastern sector, high accumulation rates can prevent multi-annual melt features from dominating the GPR reflections at shallow depths (<50m).
2. Arctic Circle Traverse 2010
Our study took place in the southeast sector of the Greenland ice sheet (Fig. 1), where few field investigations have been reported, mostly due to high accumulation rates in this region that discouraged long-term climate-data collection. We conducted the 500 km Arctic Circle Traverse 2010 (ACT-10) by snowmobile, starting at the Dye-2 station (now called ‘Raven’) and moving toward the southeast ice-sheet margin. The data presented here were collected from 26 April to 9 May 2010, prior to surface melting that could have confounded propagation of the radar signal into the subsurface. ACT-10 repeated and extended the first ACT from 2004, which crossed the ice divide at the location ‘Saddle’ (Reference Spikes, McConnell and BantaSpikes and others, 2007). In 2010, three 50 m firn cores were collected (Table 1), and surface-based GPR was used to track continuous IRHs between the core sites. Our transect is located >110km away from the open ocean. Surface mean temperature is -19.3 ± 0.28C (Reference Box, Yang, Bromwich and BaiBox and others, 2009), obtained from the NASA-SE weather station which is located ∼55 km north of ACT10-C (see Fig. 1). The mean wind speed recorded by the NASA-SE weather station is 5.5 m s–1, and its dominant direction has an azimuth of 3158 (Reference Steffen and BoxSteffen and Box, 2001), which is characteristic of the katabatic wind flow regime that is prevalent in this sector of the ice sheet. While GPR data were collected on the return segment of the traverse from ACT10-A to Dye-2 (250 km), this study focuses on the lowest-elevation eastern segments between ACT10-A and ACT10-C (Fig. 1) where the accumulation rates have been predicted to be the highest (Reference BurgessBurgess and others, 2010; Reference RaeRae and others, 2012).
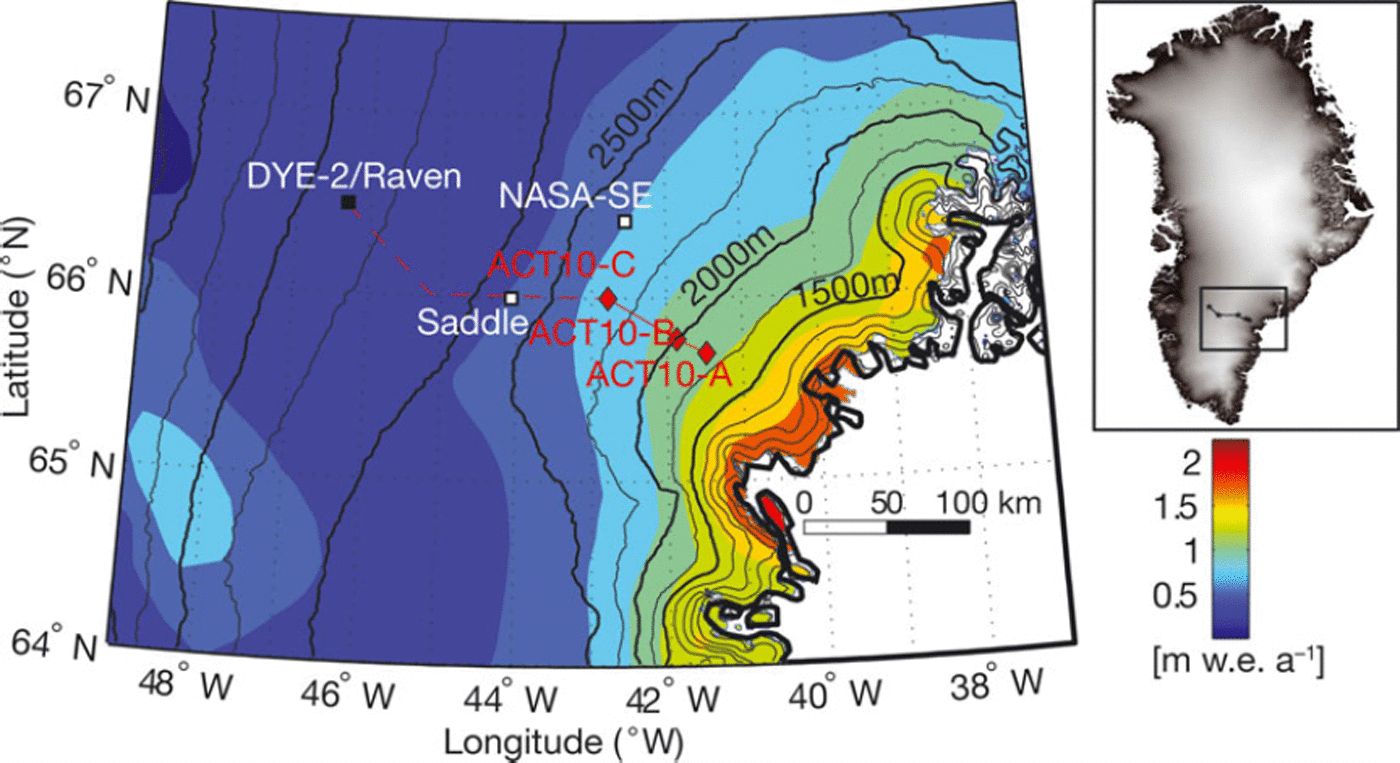
Fig. 1. Study site in southeast Greenland with the ACT-10 route, which started at Dye-2 (black square). The red solid line represents the 70 km GPR data presented in this paper. The red dashed line represents the rest of the traverse route, which is not discussed here. The red diamonds are the locations of firn cores drilled as part of this project. The black lines are elevation contours with 250m spacing from Reference Bamber, Ekholm and KrabillBamber and others (2001). NASA-SE and Saddle weather stations are represented by white squares. The background is the mean (1958–2008) accumulation rates (mw.e.a–1) modeled by Reference BurgessBurgess and others (2010).
Table 1. ACT-10 firn cores. Mean annual accumulation rates are given with one standard deviation for firn cores and for calibrated Polar MM5, representing the range of the annual values in each time series. Calibrated Polar MM5 and firn-core mean accumulation rates are calculated from the bottom age of each firn core until 2008

The ACT-10 traverse route covered a relatively slow-moving portion of the ice sheet. Observed surface velocities, for 2008-09, are in the 50-100 m a- 1 range, between ACT10-C and ACT10-A (Reference Rignot and MouginotRignot and Mouginot, 2012). We determined the flowline direction based on surface-elevation contours from the digital elevation model produced by Reference Bamber, Ekholm and KrabillBamber and others (2001); our GPR profile is approximately parallel to the current flow direction. The average ice thickness along the ACT10-A to ACT10-C transect is 1 5 2 0 ± 4 . 5m (Reference Leuschen and AllenLeuschen and Allen, 2011). Here we assume that the observed structure of the IRHs is only due to variations in accumulation, and not due to ice dynamics. This simplification can be made because of the high accumulation in this area and the minimal internal deformation at these depths corresponding to a short period of time analyzed (1995-2010).
3. Methods
3.1. Firn cores
Three 82 mm diameter firn cores (ACT10-A, -B, -C) were drilled with an ECLIPSE drill (designed by Icefield Instruments Inc.), starting 2 m below the surface in a trench to allow room for core-barrel clearance. The upper 2 m were sampled manually using the core barrel. In the field, ∼1 m core sections were labeled and bagged before being shipped frozen to the Desert Research Institute Ultra-trace Chemistry Laboratory. The core sections were then processed and analyzed for a broad range of elements and chemical species, which were used to develop a precise depth-age relationship and annual accumulation rates (Table 1). First, the cores were cut into rectangular samples, each ∼ 1 m x ∼ 3 5 m m x ∼ 3 5 m m . The samples from each site were weighed, used for the depth-density profile and then analyzed using a continuous flow analysis system with an effective depth resolution of ∼10mm (Reference McConnell, Lamorey, Lambert and TaylorMcConnell and others, 2002; Reference Banta and McConnellBanta and McConnell, 2007; Reference McConnellMcConnell and others, 2007). This system is composed of two high-resolution inductively coupled plasma mass spectrometers and a number of fluorimeters, spectrophotometers and other instruments (Reference Banta and McConnellBanta and McConnell, 2007). Indicators of continental dust (Al, Mg, Ca, Fe), sea salts (Na, Mg, Ca, S), industrial pollution (Pb, Tl, Cd, S, nitrate), explosive volcanism (S), biomass burning (black carbon, ammonium, nitrate) and atmospheric photochemistry (hydrogen peroxide (H2O2)) are used for annual-layer counting since most, if not all, of the chemical proxies show pronounced annual cycles in concentration. In regions with high accumulation rates such as southeast Greenland, H2O2 is often the preferred proxy because of its distinctive annual concentration cycle and consistent midwinter minimum (Reference McConnell and BalesMcConnell and Bales, 2004). Here we relied primarily on the annual H2O2 cycle for annual dating but secondarily used chemical proxies to confirm annual-layer identification in the few cases of unclear H2O2 cycles. The most commonly used secondary proxy was the non-sea-salt sulfur to sodium ratio (nssS/Na), which showed a very strong annual cycle due to the occurrence of anticorrelated annual cycles in the nssS and Na species. Over the southeast sector of the ice sheet, extensive summer melting, revealed by the presence of thick ice layers (>10cm), has the potential to disrupt firn stratigraphy. Accumulation from one year may percolate down and refreeze in a different annual layer, confounding water equivalence measurements using annual glaciochem-ical signals. However, in our study area, accumulation rates are generally high enough and percolating surface meltwater penetrates less than the full depth of a given year’s accumulation. Because of the multiple chemical parameters available and the high snow accumulation rate, the maximum dating uncertainty is estimated to be 1 year.
An annual depth-age relationship is deduced from chemistry-peak identification and, a posteriori, is used to test for isochronal accuracy in the GPR profile between two firn cores. Since the H2O2 peak does not occur at the exact beginning of the year, a fractional year, with 0.1 year resolution, is required to capture the full variability in snow accumulation. To convert the snow depth to accumulation at each core site for each year, an exponential function is fit to the density profile (see Section 3.3 for further details on density analysis).
3.2. GPR and GPS data
The GPR system used for ACT-10 was the Geophysical Survey Systems, Inc. (GSSI) SIR-3000 controller and a 400 MHz center frequency antenna, with an 800 MHz bandwidth. The estimated vertical resolution for the dry Antarctic firn is ∼ 3 5 cm (Reference Arcone, Spikes, Hamilton and MayewskiArcone and others, 2004; Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004), which is less than the thickness between two annual layers in our study area. The sampling interval was set at 6 traces s–1, 2048 vertical samples per trace. As the expedition moved across the ice sheet at ∼3ms– 1 , the deduced trace spacing is ∼0.5 m. In addition, to increase the signal-to-noise ratio, an initial stacking of 6 traces was performed. A time-dependent gain was used to compensate for signal attenuation by the firn. The time window was 500 ns, with 2048 samples trace-1, giving a sampling interval of ∼0.24 ns, with an average penetration depth of ∼45 m.
In post-processing, additional horizontal spatial averaging was done by stacking 8 traces, in addition to the original stacking of 6 traces in the field; thus each final trace has been averaged from 48 initial traces. This spatial averaging aims to increase the signal-to-noise ratio and minimize the influence of layer variations and cm-scale vertical ice layers present in the percolation zone, as described by Reference Humphrey, Harper and PfefferHumphrey and others (2012).
Coupled to the GPR measurements, a Trimble R7 geodetic-quality GPS receiver was used to track the location of the GPR profile every 5 s, corresponding to one point for ∼15 m (for a travel speed ∼ 3 ms–1). The GPS receiver was mounted on the snowmobile towing the GPR sled. Each GPR trace is georeferenced using processed GPS data that have been interpolated based on the time when GPR data collection began (obtained from the kinematic GPS receiver) and the trace acquisition rate. GPS data processing was done using the Canadian Spatial Reference Service Precise Point Positioning (CSRS-PPP). This processor uses GPS orbit and clock information to enhance positioning precisions in the International Terrestrial Reference Frame (ITRF) via a kinematic processing mode. Uncertainties in the GPS positions are given within one standard deviation for the ACT10-A to ACT10-C transect. The maximum standard deviations are 0.07 m for latitude and longitude (∼0.02 m on average) and 0.22 m for elevation (∼0.06m on average).
3.3. Accumulation-rate calculation
Depth-age profiles from three firn cores collected along the GPR profile (Fig. 2) are used to confirm that the IRHs are isochrones (see Section 4.3 for details on isochronal accuracy). Only the most prominent IRHs, which were the easiest to trace in the GPR profile, were used for digitizing (Fig. 2). Manual layer picking was preferred because it provided better operator control when IRHs were laterally discontinuous. While manually picking, if a short lateral discontinuity (<100 m) was observed in the GPR profile, the operator used the two IRHs located directly above and below the tracked IRH as a guide to estimate the tracked IRH depth. Three possible explanations for the partial disruption of an IRH are: (1) Topographic undulations on the surface of the ice sheet may result in more pronounced folds at depth (Fig. 2), which can induce a two-way-travel time (TWT) phase delay of as much as half the wavelength for only a 0.48 incidence angle for a given dip that reduces return strengths and causes destructive interference (Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004). (2) The presence of ice layers, due to heterogeneous meltwater infiltration, may disrupt the lateral continuity of an IRH (see Section 4.2 for details). (3) The surface roughness can cause vertical artifacts (e.g. when the radar sled lost contact with the snow surface due to sastrugi, making the IRHs more difficult to track).

Fig. 2. GPR profile between ACT10-A and ACT10-C. A total of seven different IRHs (white dashed lines) are tracked for the entire radar profile. Each isochronous layer is dated using the depth–age scale at the three core sites, and an averaged fractional age is obtained (white characters). Firn-core sites are represented by white vertical lines. ACT10-A and ACT10-C are on the left and right side of the profile, respectively. The depth scale represented on the vertical axis is calculated from the TWT–depth conversion (see Section 3.3) for the ACT10-A firn core. The black line corresponds to the elevation profile associated with the GPR profile.
For an individual digitized radar horizon, several steps are required to obtain accumulation rates. At each firn-core site, the conversion of the radar TWT to distance below the surface is computed based on the core-density profile, through the relationship between velocity in the firn, vf, and firn density profile, p(z) (Reference Kovacs, Gow and MoreyKovacs and others, 1995):
where c represents the speed of light in a vacuum, and e’ is the real part of the dielectric constant (permittivity).
The density profiles for the ACT-10 firn cores (Fig. 4) were derived from ∼1 m sections of the firn core (Section 3.1). We used an exponential fit to smooth and interpolate the density profile with depth:
where ps is the density at the surface, a and /3 are the fitting parameters and z is the depth of the profile (Reference Horhold, Kipfstuhl, Wilhelms, Freitag and FrenzelHorhold and others, 2011).
This fitted density profile is used for the TWT-depth conversion. Estimated snow depth for the radar signal is known at each core site and then linearly interpolated along the transect for each radar trace. To account for all three firn cores, we made two linear interpolations of the density profile, one between ACT10-A and ACT10-B and the second between ACT10-B and ACT10-C.
To determine the snow accumulation rate between two time periods, the depth of the upper horizon is subtracted from the depth of the lower horizon. The calculated snow thickness is then converted to a water equivalent depth using the interpolated density profile for each trace.
For defining each time period, absolute ages are assigned to an IRH from the three firn cores’ depth-age scale. A conventional way to express the age of a tracked isochrone is to use the calendar year, which is reasonable in areas with low accumulation where isochrones are closer together (e.g. Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004). In the southeast sector of the ice sheet, high accumulation rates allow us to express the age of each IRH in fractional years, increasing the precision of the accumulation-rate calculations. The GPR-derived annual accumulation rates depend primarily on the age of each tracked IRH. The estimated seasonality (fractional year) for different IRHs (Fig. 2) is not consistent from one horizon to another, varying from 0.2 to 0.7 years.
4. Results
4.1. GPR-derived accumulation rates
Mean accumulation rates, derived from the firn cores, at each core site are 1.26, 1.09 and 0.83 m w.e. a- 1 for ACT10-A, ACT10-B and ACT0-C, respectively (Table 1). They are in agreement with the accumulation rates estimated by the calibrated Polar MM5 on the pixel corresponding to each core site (Table 1). Accumulation rates are calculated along the traverse from ACT10-A to ACT10-C, from the radar profile (Fig. 2) over different time periods (Fig. 3). They are smoothed to remove digitizing noise with a moving-average filter that was 20 traces wide. The accumulation rates presented for each period highlight an increasing trend in accumulation as elevation decreases, closer to the southeast ice margin. On average, a 52% increase in accumulation (+0.43 m w.e. a-1) is observed along the 70 km line between ACT10-C and ACT10-A for the 1992.2-2008.5 time period. The spatial variability in accumulation rates over this period has a standard deviation of 0.13 m w.e. a-1. A maximum local spatial variability in accumulation is found over a 7 km distance, with 0.24 mw.e. a-1 representing 23% of the annual mean (Fig. 3). As for temporal variability, an increase in accumulation may be expected in recent decades due to the increase in surface temperature (Reference BoxBox and others, 2013). However, we found no significant trend in accumulation rate from the firn cores over their respective time periods spanning the last 25-35 years.

Fig. 3. Temporal and spatial variability in snow accumulation rates for six time periods revealed by GPR profiling between firn cores ACT10-A and ACT11-C; the thin black line represents the averaged accumulation for the whole time period 1992.2–2009.3. The thick black line represents the elevation profile. The four gray-shaded vertical bars illustrate four examples, along the GPR profile, of the presence of high-accumulation peaks located in topographic depressions, highlighting the role of wind redistribution of snow.
The wide range (∼0.26 m w.e. a-1 on average) of accumulation rates between the different time periods (Fig. 3) is mainly due to the presence or absence of an anomalous accumulation year. For example, 2003 is known to be a high-accumulation year (Reference BoxBox and others, 2005). The high accumulation over the 2002.2-2006.2 period is primarily driven by the anomalously high accumulation of 2003. In contrast, the 2006.2-2008.5 period is the lowest-accumulation period.
4.2. Influence of ice layers
Firn-core dating and GPR-derived accumulation rates are challenged by the increase in surface melt as meltwater penetrates the firn layer and refreezes. For the firn-core dating, at core sites such as ACT10-A (1825 m), accumulation rates are high (1.26 m w.e. a-1) and meltwater penetrates less (∼20%) than the full depth of the present year’s accumulation. For the IRH tracking on the GPR profile, the spatial variation of the density is difficult to estimate in the percolation zone because of heterogeneous water infiltration at small scales (∼1-5 m) (Reference Humphrey, Harper and PfefferHumphrey and others, 2012). The presence of thicker ice layers at lower elevation (i.e. ACT10-A) is illustrated in Figure 4 where the ∼1 m density measurements deviate most from the exponential fit. It becomes more difficult to track IRHs at greater depths (3545 m) as the surface elevation decreases and thicker ice layers become more common. By contrast, near ACT10-C we find more laterally homogeneous IRHs with few ice layers (Fig. 2). Understanding how firn stratigraphy affects the GPR signal is beyond the scope of this study, even if it remains an important upcoming challenge while mapping annual accumulation rates. These issues have been discussed for West Greenland by Reference Brown, Harper, Pfeffer, Humphrey and BradfordBrown and others (2011).

Fig. 4. Approximately 1 m density measurements made at each firn-core site associated with colored lines representing the exponential fit. Fitted-density profiles are used for the TWT-depth conversion and accumulation-rate estimation in water equivalent (Section 3.3). Correlation coefficients, r2, are associated for each firn-core site. Lower correlation coefficients indicate that short-scale density fluctuations increase.
4.3. Uncertainty estimates
Different sources of uncertainty affect the estimation of the IRH depth and therefore the estimation of GPR-derived accumulation rates:
-
1. The vertical density profile at each core site is estimated from the mass of ∼1 m firn-core segments (Fig. 4). To avoid bias from a single core segment dominated by ice layers, we use an exponential fit to the density profile. A fitted density profile is needed especially at lower-elevation sites where intense melt layers are interspersed with lower-density firn, producing a sporadic depth-density series (Fig. 4). The lowest correlation coefficient of determination, r2, between the exponential fit and the density-depth data is 0.87 at ACT10-A. The root-mean-square errors (RMSEs) for ACT10-A, ACT10-B and ACT10-C are 37.63, 26.12 and 12.21 kgm–3, respectively. A higher RMSE is expected for the presence of thick ice layers, with the original data deviating more from the fitted profile. Using an averaged RMSE (25.3 kgm–3), deviating at 4% from an averaged density, we obtain an average depth uncertainty of ±24 cm from the surface to the depth of the deepest tracked IRH (∼35 m).
-
2. In addition to the vertical exponential interpolation of density, an uncertainty is introduced while interpolating the density profile horizontally between two core sites. Snow stratigraphy and implied density are spatially variable at a meter scale, specifically in the percolation zone with the presence of heterogeneous infiltration forming ice layers and potential vertical channels by refreezing. By interpolating the density profile between two firn-core sites and stacking radar traces, the uncertainties are minimized. While comparing the fitted density profiles, the maximum standard deviation obtained is 31.18 kg m-3 between the ACT10-A, ACT10-B and ACT10-C fitted density profiles, yielding an average depth uncertainty of ±28 cm.
-
3. Layer picking and digitizing are performed manually, making the uncertainty difficult to quantify. Most of the IRHs observed comprise distinct wavelets with consistent phase polarity sequence: negative/positive/negative, corresponding to a 1.5 wavelet cycle (Reference Arcone, Spikes and HamiltonArcone and others, 2005b). Deduced from the 1.5 cycle wavelet length, the GPR vertical resolution (separation of two IRHs) is ∼35 cm for the dry polar firn, with the wavelet response characterizing a single interface (Reference Arcone, Spikes, Hamilton and MayewskiArcone and others, 2004). Along the ACT-10 transect, assuming that we are tracking the same IRH, the maximum 1.5 cycle wavelet lengths were ∼10 vertical samples, ∼2.5 ns or ∼25cm, which is less than the 35 cm vertical resolution of the GPR. Ideally, the high accumulation rates in this area create sufficient vertical separation between annual layers that it becomes possible to track an IRH for most years. Even for the lower-accumulation site, the minimum annual firn layer thickness is 73.2 cm, more than twice the vertical resolution of the GPR.
-
4. The age of an IRH is given at ± 1 year from the firn-core chemistry dating. Then, despite this 1 year uncertainty in the absolute age, the isochronal accuracy of the IRHs is determined at the three ACT-10 core sites. The age of a continuous IRH is determined at each end of the radar profile, using the depth-age scales from the firn cores. The difference between the two years at each side of the radar profile (ACT10-A and ACT10-C) is calculated to give the precision of this isochronal tracking. The firn core between the two end points (ACT10-B) is used to confirm the result. The mean difference of the IRHs tracked for this GPR profile is ±0.14 years, with a maximum difference of 0.37 years, indicating that the IRHs are continuous and isochronal.
Finally, we estimate an average total depth uncertainty of 37 cm from the density vertical uncertainty (point 1 above) and the density horizontal uncertainty (point 2 above), using an orthogonal error propagation law, giving a ∼20% (±0.23 m w.e.) uncertainty in the GPR-derived accumulation rates for an averaged density (640kgm–3). We did not include the core-dating uncertainty in this estimate, given the fact that each tracked IRH ends up with almost the same age (point 4 above) at the three firn-core sites along the profile and we are estimating the uncertainty of the accumulation rates derived from the technique of GPR interpolation between dated cores.
5. Discussion
5.1. Comparison with a regional climate model
The ACT-10 accumulation rates are compared to modeled accumulation-rate output from Polar MM5, which was calibrated to existing firn-core data by Reference BurgessBurgess and others (2010). Calibrated Polar MM5 is favored in this study because it accounts for orographic precipitation that other modeled accumulation outputs underestimate (Reference BurgessBurgess and others, 2010). The gridcells closest to the traverse line are used to produce an accumulation profile between ACT10-A andACT10-C. Here we focus on two IRH intervals with low and high accumulation rates (years 2006.2-2008.5 and years 2002.2-2006.2, respectively) and an interval from the bottom IRH to the surface to provide a long-interval average accumulation record (years 1992.5-2008.2). These three periods show spatial and temporal differences in accumulation from the GPR profile (Fig. 5). For the 1992.5-2008.2 period, calibrated Polar MM5 accumulation rates are in agreement with our fitted GPR-derived accumulation rates (Fig. 5). However, the 24 km grid resolution of the model does not resolve the ∼ 1 0 km and smaller-scale variation in accumulation. Examining a shorter period from 2002.2 to 2006.2, the calibrated Polar MM5 underestimated accumulation by ∼ 2 0% (∼0.24±0.16mw.e. a–1) at the highest-accumulation (and lowest-elevation) site (Fig. 5). The linear fit to the ACT-10 accumulation is steeper than the fit to calibrated Polar MM5. We think this is a consequence of the limited horizontal resolution of Polar MM5 (24 km) and/or the calibration methods used by Reference BurgessBurgess and others (2010). However, for the period 2006.2-2008.5, calibrated Polar MM5 overestimates accumulation. The maximum RMSE associated with the GPR-derived results is 0.17 mw.e. a-1 for the period 2002.2-2006.2. This value is in agreement with the calibrated Polar MM5 error estimate, which is 0.16 m w.e. a- 1 along the entire traverse route, verifying the model prediction over the southeast ice sheet.

Fig. 5. Comparison between calibrated Polar MM5 (solid line) and accumulation rates derived from GPR (solid curves), along the GPR transect, for three different time periods, showing the accumulation-rate variability. The periods chosen are the lowest (green) and highest (red) mean accumulation rates and the long-term average (blue). A linear fit (dashed line) is added for each period. The same time-span is used for calibrated Polar MM5 and GPR accumulation rates.
5.2. Local topographic influence
Accumulation rates are higher in topographic depressions (shaded bars in Fig. 3). Some combinations of wind redistribution of snow and water-vapor flux likely create this accumulation pattern. Over the Antarctic ice sheet, Reference King, Anderson, Vaughan, Mann, Mobbs and VosperKing and others (2004) showed that topography, snow precipitation, wind direction and speed resulted in significant snow redistribution that leads to high spatial variability in snow accumulation over distances as short as a few kilometers. The degree to which surface slope and accumulation rate correlate depends on how the GPR profile is oriented relative to the direction of the dominant wind (Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004; Reference Arcone, Spikes and HamiltonArcone and others, 2005a). In our study region, wind direction is essentially from ∼315° (from the NASA-SE station), which is on average parallel to the GPR profile. But, for the last 10 km of the study transect (toward ACT10-C), the main wind direction may diverge up to ∼30° from the GPR profile direction. This difference could explain amplitude differences and a slight phase shift between the accumulation rates and the surface-slope derivative (Fig. 6).

Fig. 6. Comparison between convexity/concavity index (red) and the detrended annual accumulation rate from the radar (blue) for the ACT10-A to ACT10-C transect. To calculate the convexity/concavity index, outliers were removed and a Gaussian smoothing function was applied, with 1<J width of the Gaussian equal to ∼0.2 km (a=70.5 GPR horizontal traces).
The second derivative of the surface-elevation profile yields the topographic curvature corresponding to the convexity or concavity of the terrain. Positive values represent concavity, where the terrain has a local depression, and negative values represent convexity, where the terrain has a local high (Fig. 6). The GPR-derived accumulation rates were detrended to remove the overall increasing accumulation rate along the studied transect. This convexity/ concavity index shows good agreement with the accumulation pattern. Higher accumulation correlates with concavity (positive values), with a correlation coefficient of r2 = 0.330 (Fig. 6).
Although the amplitude and local maxima/minima shifts between accumulation values and the convexity/concavity of the terrain do not correlate perfectly along the entire profile, it is generally true that the GPR-derived accumulation rates are lower if the surface is convex and higher if it is concave. This pattern is consistent with wind scouring from the tops of undulations and redeposition into adjacent depressions (or else there is less scouring in depressions). Here scouring refers to some combination of sublimation loss and wind redistribution.
5.3. Temporal variability
Temporal variability is investigated here using only the firn cores and is compared to the calibrated Polar MM5 (Table 1). We find that the GPR data do not clearly resolve annual accumulation rates because of the difficulty in tracking IRHs due to the increasing presence of ice layers as elevation decreases. The agreement between the averaged firn-core accumulation rates and the accumulation rates from calibrated Polar MM5 over corresponding time periods is characterized by correlation coefficients, r2, ranging from 0.39 to 0.65, and RMSE ranging from 0.11 to 0.25 m w.e. a–1 (Fig. 7). At the lowest-elevation core site, ACT10-A, the calibrated Polar MM5 underestimated the mean accumulation rate by 5% (0.06mw.e. a–1).

Fig. 7. Comparison of the temporal variation of accumulation between Polar MM5 (red) and firn cores (blue), for each core site, from low elevation to high elevation, ACT10-A, ACT10-B and ACT10-C, respectively. Dashed lines present a linear fit to the data for Polar MM5 (red) and firn cores (blue). There is a change in vertical scale between cores.
Atmospheric reanalysis and ice-core data indicate an increase in snow accumulation rates on the ice sheet since 1958 (Reference HannaHanna and others, 2008; Reference BoxBox and others, 2013). However, no significant increasing temporal trends were identified over the length of our ACT-10 firn-core records. The ACT-10 cores are <40 years in duration and seem dominated by high interannual variability (Fig. 7). An observation from Figure 7 reveals the presence of year 2003 as a strong positive accumulation anomaly, in ACT-10 firn cores. This high-accumulation year was related to persistent low atmospheric pressure on the southern tip of the ice sheet from September 2002 to April 2003 (Reference BoxBox and others, 2005). During this time period, large accumulation events are recorded by automatic weather stations, such as NASA-SE (located ∼55 km north of ACT10-C). For example, one event deposited 65 cm of fresh snow over 7 hours followed by strong winds compacting the snowpack down to 40 cm (Reference BoxBox and others, 2005). High-accumulation years like 2003 have implications for the following summer melt rates by maintaining a higher albedo, minimizing the impact of observed warming (e.g. Reference Box, Yang, Bromwich and BaiBox and others, 2009) on increased melting.
The interannual variability observed in the firn cores is high, especially at the lowest-elevation site (ACT10-A) with a standard deviation of 0.373 mw.e. a- 1 (∼30% of the mean). The calibrated Polar MM5 data at the corresponding gridcells have standard deviations of 0.152, 0.123 and 0.084 m w.e. a- 1 for ACT10-A, ACT10-B and ACT10-C, respectively (Table 1). This interannual variability in the southeast is large enough to significantly impact the total mass budget of the entire ice sheet, accounting for ∼ 3 0% of the ice-sheet total interannual variability in accumulation (Reference BurgessBurgess and others, 2010).
However, the modeled accumulation rates show ∼ 5 0% less variability compared to the firn cores. The Polar MM5 interannual variability is lower than the firn-core observations because of the month-long model integration (Reference BurgessBurgess and others, 2010), producing ∼ 3 0% lower interannual variability in Polar MM5 than in earlier configurations in which daily integrations are made (Reference BoxBox and others, 2006). In addition, this interannual variability discrepancy between the firn core and the model can be explained by the large model horizontal grid resolution compared to the point measurements of the firn cores. At the firn-core site, spatial variations due to wind redistribution result in incoherent ‘glaciological noise’ (Reference Mosley-ThompsonMosley-Thompson and others, 2001) in the firn-core data that is also not captured by a 24 km gridcell of Polar MM5. To reduce this incoherent noise, a common practice is to use multi-year average filters (Reference Banta and McConnellBanta and McConnell, 2007). However, despite minimizing incoherent noise, these filters eliminate some of the high-frequency coherent signal, such as the presence of anomalous high-accumulation years (e.g. 2003). We find correlation coefficient values between firn cores of r=0.84 for ACT10-A vs ACT10-B; r= 0.75 for ACT10-A vs ACT10-C; and r=0.88 for ACT10-B vs ACT10-C, all associated with <10–5 p-values, which are statistically significant (at p<0.01), for common time periods. These relatively high correlation coefficients (r>0.75) between firn-core time series support the finding that both the firn cores and calibrated Polar MM5 capture a common climate.
Comparing a regional accumulation record with a large-scale atmospheric circulation pattern is a commonly used process to identify precipitation source regions as well as understand how the observed interannual variability may affect the annual surface mass-balance estimates (e.g. Reference Mosley-Thompson, Readinger, Craigmile, Thompson and CalderMosley-Thompson and others, 2005). The North Atlantic Oscillation (NAO), a dominant mode of regional atmospheric variability around Greenland, exerts a significant yet complex spatial and temporal influence on Greenland precipitation (e.g. Reference Appenzeller, Schwander, Sommer and StockerAppenzeller and others, 1998; Reference Hutterli, Raible and StockerHutterli and others, 2005; Reference Mosley-Thompson, Readinger, Craigmile, Thompson and CalderMosley-Thompson and others, 2005; Reference Banta and McConnellBanta and McConnell, 2007). The NAO is the difference in atmospheric pressure at sea level between the Icelandic-low pressure system and the Azores-high pressure system, and indicates changes in the intensity and direction of the North Atlantic storm tracks (Reference HurrellHurrell, 1995). The influence of the NAO on accumulation varies spatially and temporally for the Greenland ice sheet (Reference Mosley-Thompson, Readinger, Craigmile, Thompson and CalderMosley-Thompson and others, 2005). Reference Hutterli, Raible and StockerHutterli and others (2005) identified four regions over the Greenland ice sheet with distinct sources of accumulation variability, with only the western sector of the Greenland ice sheet presenting an inverse relationship with a NAO pattern. The other regions are affected by other large-scale patterns (e.g. the southeast region, where accumulation is positively correlated with a high-pressure anomaly over the Greenland Sea).
Despite the short time-span of the cores (last 25-35 years), a comparison between the firn-core records and the December-March NAO index of Reference HurrellHurrell (1995), consistent with Reference BoxBox (2005), shows a negative correlation. Using this seasonal NAO index gives a ∼0.2 higher correlation compared to using the annual NAO index. While the correlation coefficients are low - r=-0.21 for ACT10-A, r=-0.25 for ACT10-B, and r=-0.38 for ACT10-C - their p-values (1 - p ranging from 0.68 to 0.98) suggest that the captured signal is real. Reference Mosley-Thompson, Readinger, Craigmile, Thompson and CalderMosley-Thompson and others (2005) demonstrated that the use of a temporal smoothing filter (5 year triangular filter) improved the correlation coefficients. Applying this filter to the ACT-10 firn-core data, we find a similar result with higher correlation coefficients: r=-0.40 for ACT10-A, r=-0.33 for ACT10-B, and r=-0.59 for ACT10-C. These low initial correlations may imply that the origin of moisture source in the southeast is not explained by the NAO alone.
6. Conclusions
The presence of three new annual accumulation records from our ACT-10 cores, as well as spatial accumulation rates from our GPR profile, provide necessary in situ measurements in the southeast sector of the Greenland ice sheet. Since the accumulation rate at our study site was greater than the vertical resolution of our GPR system, we expected to be able to track annual reflection horizons in our GPR profile. While this was possible at higher elevations along our transect, we found that it was not always possible at lower elevations because the presence of >10 cm thick melt layers likely caused spatial discontinuity of IRHs.
The obtained in situ measurements of accumulation would contribute to further validation efforts and help reduce Greenland accumulation model uncertainties in the southeast sector, where accumulation rates are the highest on the ice sheet. Radar profiling along a 70 km transect between our firn cores indicates a 52% (∼0.43mw.e.a–1) increase in accumulation from the higher-elevation site (ACT10-C at 2350 m) to the lower site (ACT10-A at 1830 m). Maximum spatial variability estimated from the GPR, which is not captured by widely spaced single-point measurements such as firn cores, is found to be 23% (up to 0.24 m w.e. a-1 in this case) over distances as short as 7 km. This shows that firn-core data alone may not be adequate to infer regional accumulation rates, as local topography and wind redistribution must be considered. Surface convexity is found to be a useful predictor of undulation-scale accumulation variability, with the highest local accumulation rates associated with local depressions (concavities).
No significant temporal trend exists in the firn-core data. The mean accumulation rates, of up to 1.26 m w.e. a- 1 , from the firn cores are in a good agreement with calibrated Polar MM5 output, but the amplitude of the interannual variability observed in firn cores is substantially reduced in the model output; interannual variability in the calibrated Polar MM5 is ∼ 5 0% less than measured in the firn cores. This is mainly due to a combination of ‘glaciological noise’ in the firn-core data, and the smoothing effect of using different model-integration strategies for Polar MM5. Further, the discrepancy in the interannual-variability amplitude, for the calibrated Polar MM5 and the firn cores, increases toward the coast as accumulation rates increase.
The three ACT-10 firn-core accumulation records, strongly inter-correlated (r>0.75), are likely to be affected by a common climate. Initial comparisons between the accumulation records and seasonal NAO indices show low correlations, implying that the accumulation in southeast Greenland for recent decades is likely not controlled by the NAO alone.
Acknowledgements
We thank the chief editor, Gwenn Flowers, and the scientific editor, Catherine Ritz, for comments and handling of our manuscript. We thank Reinhard Drews and an anonymous reviewer for many insights and comments that substantially improved the manuscript. This work was supported by US National Science Foundation (NSF) Office of Polar Programs award ARC-090946 and ARC-0909499. Clement Mie`ge is funded under the NASA Earth and Space Science Fellowship program. We thank Susan Zager and others at CH2M HILL Polar Services for logistical assistance, and Terry Gacke and others at the Ice Drilling and Design Office (IDDO) for ice-drilling expertise and enthusiastic help with the expedition.










