Introduction

Global warming and other ongoing changes in the Earth system are beginning to have significant impacts, not only on the physical environment, but also on the biosphere and society (Reference Dyurgerov and MeierDyurgerov and Meier, 2005). Glacier and ice-cap variations are among the most visible indications of the effects of climate change (Reference Klok and OerlemansLemke and others, 2007). This is mainly due to the clearly recognizable retreat of many large valley glaciers in response to a temperature increase of about 1 K since 1850, which is hardly noticeable otherwise (Reference PatersonPaul and others, 2007). Such glacier retreats have direct impacts on processes of global importance such as sea-level rise, the hydrology of mountain-fed rivers, the freshwater balance of the oceans, natural disasters, and even the shape and rotation of the Earth (Reference Dyurgerov and MeierDyurgerov and Meier, 2005). To make a reliable prediction on how glaciers may behave in the future, it is important to understand how glaciers reacted to climate variability in the past.

At present, the total glacier area outside Greenland and Antarctica is estimated to be (522±42)×10³ km² (Reference Paul, Kääb and HaeberliRaper and Braithwaite, 2005). Estimates of glacier and ice-cap volume are more difficult to establish, and vary between 15 and 37 cm of global sea-level equivalent (Reference Klok and OerlemansLemke and others, 2007). Glaciers in the European Alps only constitute a very small fraction of this. However, in common with many other mountain glaciers worldwide, most Alpine glaciers reached their last maximum extent between 1850 and 1900 at the end of the Little Ice Age, and retreated to near their minimum extent over at least the last several thousand years after that. A combination of in situ measurements, remote sensing and numerical modeling shows that glaciers in the European Alps lost 35% of their total area from 1850 until the 1970s, and almost 50% by 2000 (Reference WalravenZemp and others, 2006). This trend is confirmed by the new satellite-derived Swiss glacier inventory, which revealed that mean glacier area loss per decade from 1985 to 1998/99 has accelerated by a factor of seven compared to the period 1850–1973 (Reference PatersonPaul and others, 2007).

Central to studies of glacier changes is the mass balance. For the last decades of the 20th century, there is a strong negative correlation between Northern Hemispheric net mass balances and Northern Hemispheric summer temperatures (Greene, 2005). Changes in the snow accumulation also matter, and may have dominated in responses to large circulation changes or when temperature is not changing greatly (Reference Klok and OerlemansLemke and others, 2007). For example, analysis of glacier mass balance, volume change, length fluctuations and homogenized temperature records for the western part of the European Alps indicates a significant effect of precipitation changes on glacier variations during the 18th and 19th centuries (Reference VincentVincent and others, 2005).

Direct measurements of mass balance are available for only a limited number of glaciers and seldom extend far back in time. Therefore, models have to be used to extend measured mass-balance series in the future and the past. Several approaches can be used such as temperature-index models, regression models and energy-balance models (Reference Greene, Broecker and RindHock, 2005). For instance, with a simple regression model, Reference GreeneGreene and others (1999) found an upward shift of the equilibrium-line altitude (ELA) of 114 m between 1850 and 1973 for the Swiss Alps. Reference Raper and BraithwaiteSchöner and Böhm (2007) applied a linear regression model on two Austrian glaciers (Hintereisferner and Vernagtferner) to reconstruct the mass balance back to 1800. Reference SteinackerVincent (2002) used a degree-day model to reconstruct the mass balance of four French glaciers (Saint-Sorlin, Gébroulaz, Argentiére and Mer de Glace) over the 20th century. More recently, a more complex distributed temperature-index melt model coupled to an accumulation model was used to reconstruct the seasonal mass balance of four Alpine glaciers (Aletschgletscher, Rhonegletscher, Griesgletscher and Silvrettagletscher) for the period 1865–2006 (Reference HockHuss and others, 2008).

In this paper, we focus on the evolution of the annual mass balance of Vadret da Morteratsch. The annual balance is defined as the change in mass, expressed in water equivalent, on a fixed date relative to the same date in the previous year (Anonymous, 1969; Reference Palmer, Schwikowski and GaeggelerPaterson, 1994). Vadret da Morteratsch is located in the Bernina Massif in southeast Switzerland and is the largest glacier in this area. A map of the area around Vadret da Morteratsch is shown in Figure 1. A range of high mountains, such as Piz Palü, Piz Zupo and Piz Bernina, surrounds the glacier. Piz Bernina (4049 m a.s.l.), which is located in the southwest of the glacier, represents the highest point of the glacier. The glacier tongue flows down to approximately 2030 m (status in 2006). At present, Vadret da Morteratsch has a length of about 7 km and an estimated area of 16 km²; at a distance of about 2 km from the snout, Vadret Pers flows into Vadret da Morteratsch from the east. According to length measurements, Vadret da Morteratsch reached its maximum extent in 1857 and shortened by 2196m between 1878 and 2007 (Glaciological reports, 1881–2008; Reference Machguth, Paul, Hoelzle and HaeberliMaisch and others, 1999).

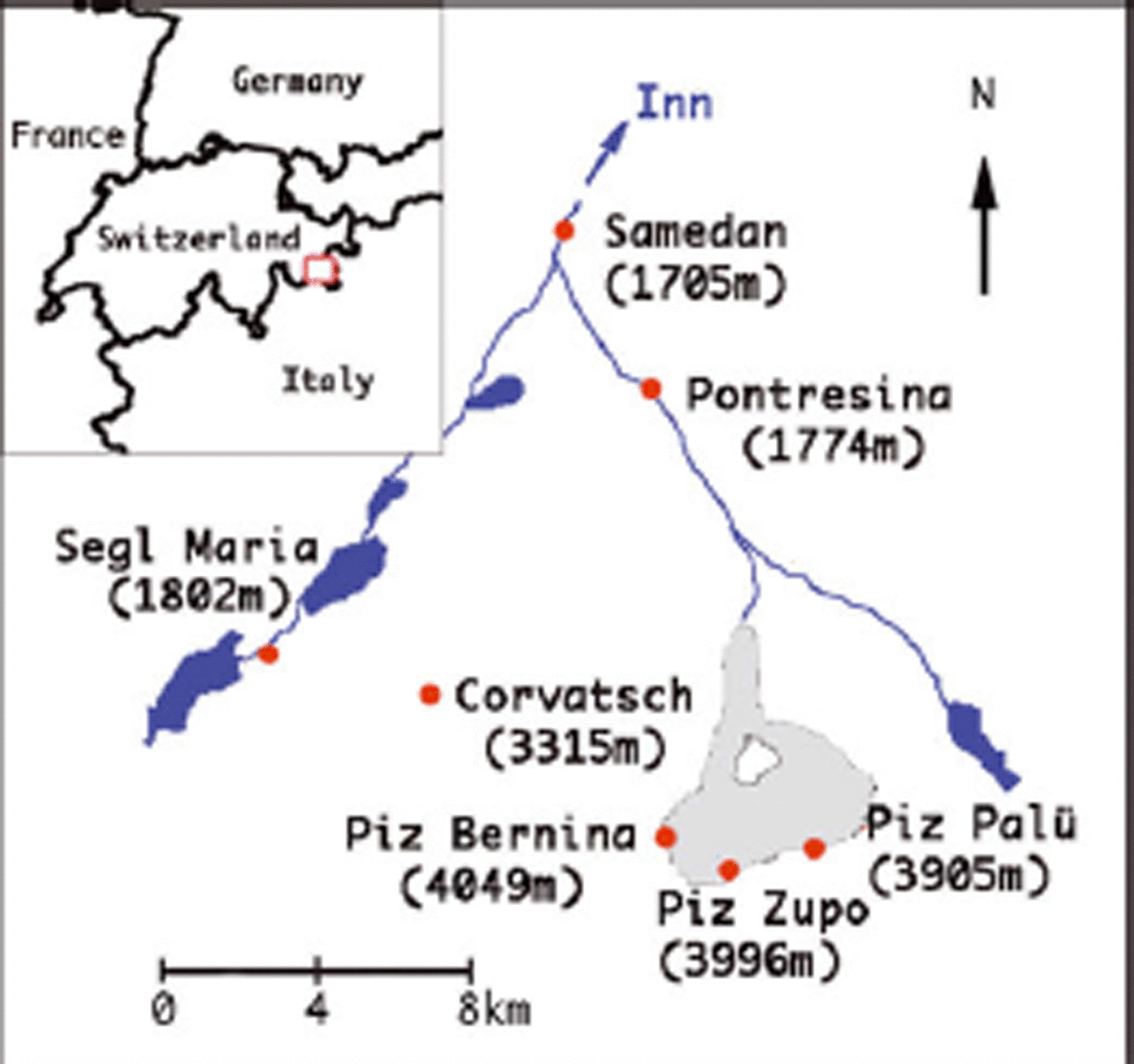
Fig. 1. Location map of Vadret da Morteratsch and its surroundings in the Engadine, southeast Switzerland. The glacier area is shown in grey in the inset. Lakes and rivers are indicated in blue

We have reconstructed the annual balance of Vadret da Morteratsch with a two-dimensional energy-balance model (Reference OerlemansOerlemans, 2001) for the period 1865–2005. A similar energy-balance model was used by Reference Lemke and SolomonMachguth (2003) to compare modeled and simulated mass balances of 14 Swiss glaciers in 2002 and to reconstruct the mass balance for Claridenfirn, Switzerland, for the period 1981–2002, using global radiation, precipitation and air temperature as input (Reference MachguthMachguth and others, 2006). A more detailed energy-balance model, using air temperature, humidity, air pressure, incoming shortwave radiation and precipitation as input, was previously applied to Vadret da Morteratsch for the period 1980–2002 (Reference KlokKlok and Oerlemans, 2002; Reference Huss, Bauder, Funk and HockKlok, 2004). In contrast to these studies, we reconstructed the surface mass balance for a longer period, starting in 1865.

This restricts the model input to precipitation and air temperature, which are the only available climate records for this longer period. The resulting cumulative mass balance is expected to be a good estimate of the total mass loss of Vadret da Morteratsch since its Little Ice Age maximum.

Field Measurements

Mass-balance measurements have been carried out at about 20 different positions on both Vadret da Morteratsch and Vadret Pers by research groups of the Alfred Wegener Institute and Vrije Universiteit Brussel since 2001. The highest measurements were made from aluminium poles and snow pits in a zone around the Fuorcla Crast’Agüzza (between Piz Bernina and Piz Zupo) at 3400–3700ma.s.l. (Fig. 2). Due to the high wind speeds in the pass area, these measurements are, however, not believed to be representative for the whole accumulation zone. These accumulation measurements were further supplemented by shallow ice-core drillings in the Crast’Agüzza saddle area in October 2002 and by a 43 m ice core drilled by a Swiss group below Piz Zupo at 3900 ma.s.l. in March 2002 (Reference Oerlemans and KnapPalmer and others, 2003). The latter ice core is believed to span a period of 11 balance years. All other measurements were carried out in the ablation area and close to the equilibrium line by classical ablation stakes. The highest of these measuring sites is close to the equilibrium line at about 3000ma.s.l., and the lowest is located close to the glacier snout at about 2110 ma.s.l. (elevation in 2001, but down to below 2050 m in 2007). The intermediate stakes are spread out over the ablation zone of both glaciers at an elevation interval of approximately 100 m. Additionally, three measurements were carried out along a transect across Vadret da Morteratsch at approximately 2550ma.s.l. to investigate the influence of shading by the surrounding mountains. Figure 2 shows the positions of the mass-balance measurements during the period 2001–06. These locations at the same time record the glacier movement over this period. Stake heights were measured at the end of the summer ablation season, usually during the first 2 weeks of October.

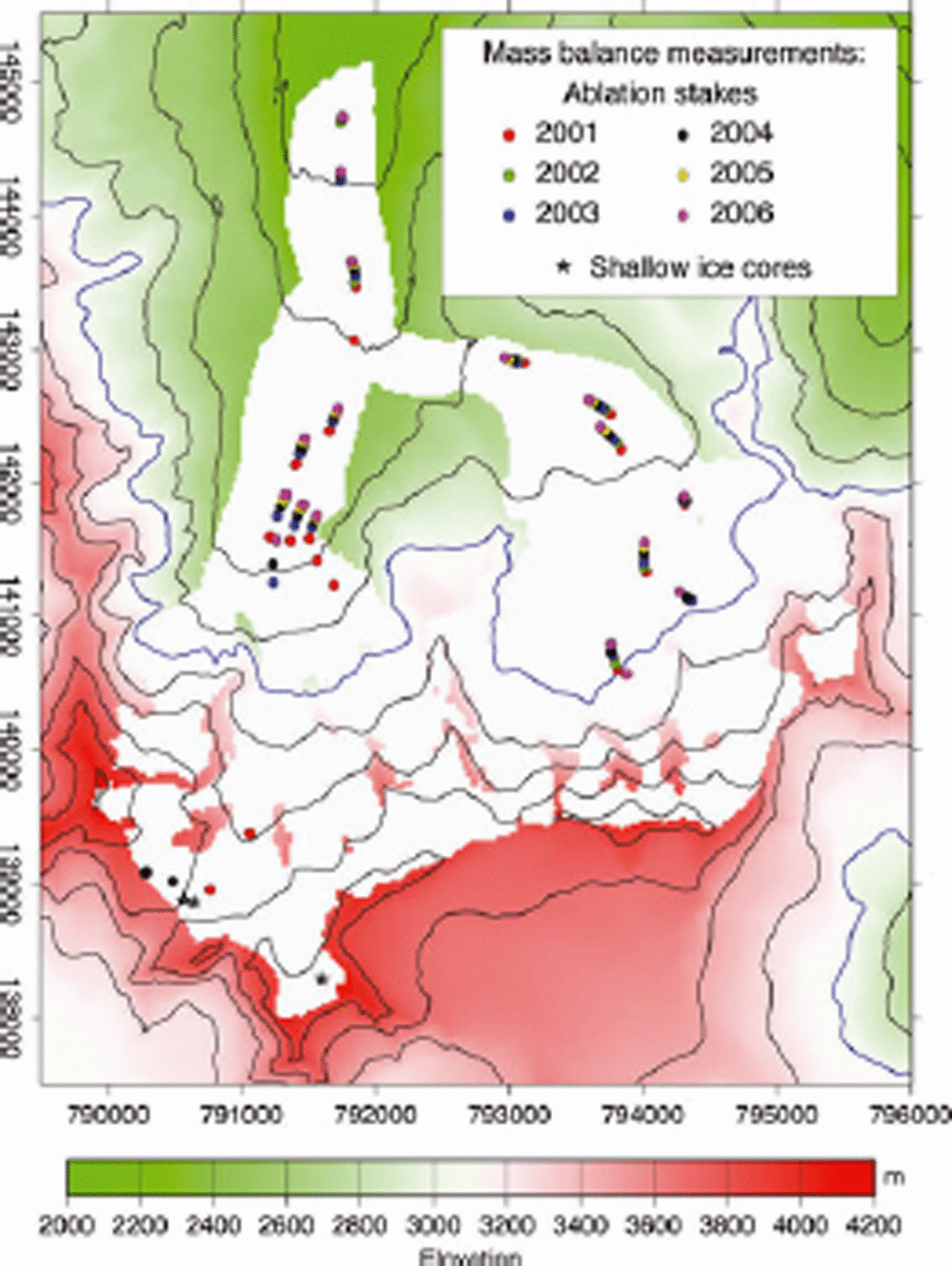
Fig. 2. Mask of Vadret da Morteratsch, together with the topography of the surrounding area and the position of all mass-balance measurements used in this study. The map coordinates are in metres from the Swisstopo coordinate system. The blue contour line is at 3000 m and is close to the ELA of recent years.

Figure 3 shows the annual balance measured at the stakes in the ablation zone, with the annual balance plotted against the altitude of the measurement site. The measurement sites higher than 2650ma.s.l. are located on Vadret Pers, and those lower than 2650 ma.s.l. on Vadret da Morteratsch. Of these five years of measurements, 2003 was the year with the highest ablation and 2004 the year with the lowest. The mean difference in ablation between these two years is about 2 mw.e., less at higher elevations and somewhat more at lower elevations, i.e. the balance gradient is steepest in the warmest year. The highest ablation measured in this record was nevertheless in 2006, with 9mw.e. at 2053ma.s.l., in part because of the continuous glacier thinning at this site and the resulting altitude–temperature feedback. In general, the mass-balance gradient along the centre line on Vadret Pers is larger than that of Vadret da Morteratsch, probably due to the shading effects of the surrounding mountains and the different orientation of the surface with respect to the sun. This effect is also very evident when looking at the large difference in ablation between the highest measurement sites on Vadret da Morteratsch and the lowest on Vadret Pers. Ablation is up to 3mw.e. larger on Vadret Pers at an altitude that is nevertheless 100m higher than the corresponding site on Vadret da Morteratsch. The shading effect is also very obvious at the measurement sites at 2530 ma.s.l. on Vadret da Morteratsch, which correspond to the lateral cross-profile on Vadret da Morteratsch (Fig. 2). The easternmost site at the margin in, for example, 2003 experienced almost 2 mw.e. less melting than the stake in the middle of the glacier at approximately the same altitude. This again can be explained by the shading effects of the surrounding mountains. Note, however, that variations in albedo can also have a large effect.

Fig. 3. Mass-balance measurements from 2002 to 2006 in the ablation zone plotted against altitude. The sites lower than 2600ma.s.l. are located on Vadret da Morteratsch and the higher ones on Vadret Pers.

Description of the Model

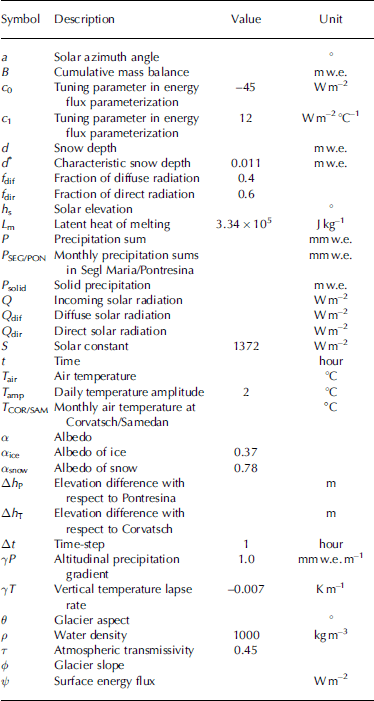
We used a time-dependent two-dimensional mass-balance model based on parameterizations for the surface energy fluxes and the evolution of surface albedo (Reference OerlemansOerlemans, 2001). The inputs for this model are: (1) a gridded digital elevation model (DEM) of 1998 containing the elevation of the glacier and the surrounding mountains as provided by the Bundesamt für Landestopographie of Switzerland on a horizontal resolution of 25 m, (2) a glacier mask containing information about form, location and size of the glacier, and (3) time series of temperature and precipitation to force the model. The variables and parameters appearing in the various formulations below are listed in Table 1 (and are not explained directly in the text).

Table 1. List of variables and constants used in the model

The model is based on an equation for the cumulative mass balance B, which represents the gain or loss of mass at an individual gridpoint at time t. The time-step Δt is 1 hour:

(1)

The term represents melting at the surface (ablation) in case of a positive surface energy flux. Sublimation is neglected, due to the very high latent heat of sublimation compared to the latent heat of melt (2.834×10⁶ J kg^–1 compared to 3.334×10⁵ J kg^–1). It is assumed that solid precipitation (snow) occurs for air temperatures below 2°C (accumulation).

To calculate the budget of the energy fluxes at the glacier surface, representations are required for incoming and outgoing shortwave and longwave radiation, turbulent heat fluxes and the heat flux supplied by rain. Since most of the parameters describing these fluxes are unknown or not readily available, it is more convenient to parameterize the net energy flux at the surface as:

(2)

where the first term on the right-hand side is the incoming radiation at the glacier surface and the term c ₀ + c ₁ .T _air is the sum of the longwave radiation balance and turbulent heat exchange (Reference OerlemansOerlemans, 2001; cf. Table 1).

The albedo parameterization distinguishes between ice and snow following the work of Reference Oerlemans and KlokOerlemans and Knap (1998). The albedo ranges between 0.78 (typical value for snow) and 0.37 (typical value for ice) and is made to decrease exponentially with the snow depth. d* is the characteristic length scale for snow depth (11mmw.e.). We estimated d^* by multiplying the depth scale found by Reference Oerlemans and KlokOerlemans and Knap (1998) by a snow density of 350 kgm^–3 (Reference KlokKlok and Oerlemans, 2002).

(3)

The incoming solar radiation Q is split up into a direct and a diffuse part:

(4)

where τ is the reduction factor of the incoming solar radiation through the atmosphere. Theoretically, the value of f _dif can vary between 0.15 for clear-sky conditions and 0.85 for overcast conditions, although the latter also depends on the type of cloud (e.g. for a uniform layer of cirrostratus f _dif can be 0.5 (Reference OerlemansOerlemans, 2001). Here a constant value of 0.4 is used for f _dif, so the value of f _dir is 0.6. The model also distinguishes between shaded and non-shaded gridcells. In the case of shade, only the diffuse part of the solar radiation is considered. In the case of no shade, both diffuse and direct radiation are considered. The solar elevation as well as the azimuth is calculated with a standard method (Reference Vincent, Le Meur, Six and FunkWalraven, 1978). The angle (Σ _s) between the sun’s projection on the horizontal plane and the plane of the gridcell’s slope is calculated as

(5)

Climate Forcing

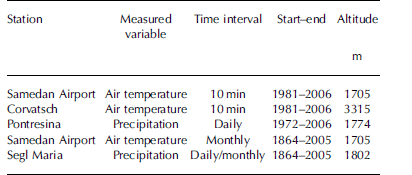
In this study, the above-described energy-balance model was applied for two different time periods, using different temperature and precipitation input. At first, detailed data from surrounding weather stations (see Table 2) were used to obtain the surface mass-balance history from 1981 to 2006 in best agreement with the observational data since 2001. This series of experiments served to calibrate the model and to investigate its basic sensitivity. Results of this calibration run are not presented here (for details see Reference Maisch, Burga and FitzeNemec, 2007), but brought to light how climatic data from surrounding stations could be treated best to optimally represent temperature and precipitation on the glacier.

Table 2. Overview of the meteorological data used to force the glacier mass-balance model

For the mass-balance reconstruction between 1865 and 2005 we employed temperature and precipitation data from the HIST-ALP dataset as climate forcing (see Table 2). The HIST-ALP database consists of monthly, homogenized records of temperature, pressure, precipitation, sunshine and cloudiness for the ‘Greater Alpine Region’ (Reference AuerAuer and others, 2007). The series from Samedan and Segl Maria were selected because those are the stations closest to Vadret da Morteratsch with homogenized long-term records. Daily precipitation and temperature data dating back to 1864 are also available for the Segl Maria station, but these series are not homogenized. Annual mean temperatures calculated from the non-homogenized daily temperatures from Segl Maria appeared to have a bias of up to 0.75°C for the period before 1980 when compared to the homogenized annual mean temperatures from Samedan. Likewise, annual precipitation amounts calculated from the homogenized monthly data from Segl Maria differed in a quasi-random way by 240 mma^–1 from those calculated from the non-homogenized daily data. This comparison shows the importance of homogenizing long-term climate series and made us favour the monthly data over the more detailed daily data. The homogenized mean summer temperatures from Samedan and annual precipitation sums from Segl Maria are shown in Figure 4.

Fig. 4. HIST-ALP climate data used to force the mass-balance model. (a) The homogenized summer temperature (May–September) record from Samedan; (b) the mean annual precipitation sums from Segl Maria. Both records date back to the 1860s.

Finally, using the long-time-series data, the parameters for the surface energy fluxes were slightly retuned. The best agreement between observed and simulated annual balance was found with the following parameters: c ₀ = –45Wm^–2, c ₁ = 12 Wm^–2 °C^–1, τ = 0.45. These values were found by comparing model results with measurements using the root-mean-square error (RMSE) as a validation criterion (Fig. 5). The comparison was performed between the measurement site and the closest model gridpoint.

Fig. 5. Comparison of simulated and measured mass balance for four balance years 2002–05. The RMSE is also shown.

Air Temperature

To estimate the surface air temperature and the lapse rate over Vadret da Morteratsch, we used temperature data from Samedan and Corvatsch. Measurements from the IMAU (Instituut voor Marien en Atmosferisch Onderzoek) automatic weather station (AWS) near the tongue of the glacier show that the high-altitude weather station at Corvatsch is best suited to estimate temperature variations on the glacier. The correlation coefficient of daily temperatures at the AWS and Corvatsch for the balance year 1994/95 is very high, 0.97 on an annual basis (Reference OerlemansOerlemans, 2001). The Samedan temperature record is less suited for this purpose because temperature inversions tend to develop in the valley during the winter. Consequently, when snow is present in the valley, the air temperature in Samedan is often lower than in Corvatsch despite a lower elevation of more than 1600 m. This ‘cold pool effect’ is not present on the tongue of Vadret da Morteratsch, where a katabatic flow mixes warmer air downwards all the time (Reference OerlemansOerlemans, 2001). Therefore the temperature distribution over the glacier was calculated starting from the Corvatsch temperature data. Nevertheless, the Samedan data were taken into account to estimate the mean temperature gradient over the glacier. Daily temperature gradients between Samedan and Corvatsch were calculated for the period 1981–2005. Only values below –0.006 Km^–1 were considered because it was assumed that for less negative gradients a temperature inversion was present. This results in a mean temperature gradient of –0.007 Km^–1.

To introduce monthly time series, several additional approximations were made. First we found a high correlation (r = 0.978) between monthly mean temperature anomalies from Samedan and Corvatsch for the period 1981–2005. This high correlation allows estimation of the mean monthly temperature at Corvatsch, and consequently on the glacier, for the period since 1865 from the long Samedan series using the lapse rate Σ _T = –0.007 Km^–1 established above. The mean daily temperature range on the whole glacier was assumed to be constant at 4°C, intermediate between the 6°C measured at the glacier tongue (Reference NemecOerlemans, 2000) and the 2°C observed at Corvatsch. Therefore, the mean monthly temperature on the glacier and its mean daily cycle were calculated as:

(6)

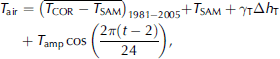
where ΔhT is the altitude difference with respect to Corvatsch. T _air is used for the calculation of the turbulent and longwave fluxes. For the threshold temperature of snow, the monthly mean temperature plus the altitudinal gradient was used.

Precipitation

The distribution of precipitation on the glacier is more complicated to handle than air temperature. Precipitation amounts in mountainous regions are spatially non-uniform and have a strong vertical dependence. Sites only a few kilometres away may receive significantly different amounts. Beside that, there are limited precipitation data available at higher elevations. For conditions high up in the accumulation zone of Vadret da Morteratsch, the ice-core measurements from Piz Zupo at 3900ma.s.l. are believed to be the most representative. Correlations were sought between these data and data from the valley stations, for the period between 1 October and 30 September of the following year, in order to be able to compare balance years. For the period 1991–2001 the mean vertical precipitation gradient between Piz Zupo and two valley stations varies from between 0.90 mmw.e.m^–1 with respect to Pontresina, and 0.97 mmw.e.m^–1 with respect to Segl Maria. Interestingly, the mean vertical precipitation gradient between Corvatsch (3315 m) and Pontresina (1774 m) is only 0.05 mmw.e.m^–1, and for some years the gradient is even negative. The reason might be an under-catchment of precipitation at the weather station on Corvatsch due to high wind speeds. We adapted a value of Σ _P = 1.0mmw.e.m^–1, as this gives the best fit with the observed annual balance data. This value is significantly higher than the precipitation gradient of 0.4–0.5mm w.e.m^–1 used by Reference KlokKlok and Oerlemans (2002) and Reference OerlemansOerlemans and Klok (2004) and the value of 0.8 mmw.e.m^–1 in Reference Lemke and SolomonMachguth (2003). The higher gradient found here might also be due to the fact that the ice-core measurement site is believed to be located in a sink area for snow blowing from across the ridge onto the glacier. From the available data we are not able to make a further differentiation of the precipitation rate with respect to wind exposure and elevation. For instance, it is known from some other high mountain glaciers in the Alps that a precipitation maximum occurs at around 3500ma.s.l., which is lower than the highest summits in our study area.

In order to apply the monthly precipitation series from Segl Maria since 1865 we calculated the ratio of mean monthly precipitation at Pontresina and Segl Maria for the overlapping period 1972–2005 and multiplied this by the monthly precipitation at Segl Maria for the whole period (1865–2005). For the period 1972–2005 the correlation coefficient (r) between the calculated and the observed monthly precipitation at Pontresina is 0.87, not as high as for the temperature series but still acceptable for our purpose. This gives the following relation to estimate monthly precipitation sums on the glacier:

(7)

where Δh _P is the altitude difference with respect to Pontresina.

The initial calibration for the period 1981–2006 using the daily precipitation data from Pontresina brought to light the large sensitivity of the net mass balance to the frequency and intensity of the precipitation events in the course of any month. The timing of the precipitation events was therefore taken from the non-homogenized daily precipitation series from Segl Maria after scaling for the mismatches of the associated monthly sums to the homogenized precipitation series from the same station. This is believed to be the best option available. Nevertheless, combining daily precipitation input with mean monthly air temperature to distinguish between snow and rain might lead to an underestimation of snowfall events, especially in the summer months. Summer snowfall episodes are known to have a large impact on the net mass balance of a glacier, due to the dependence of the albedo on snow depth (Reference OerlemansOerlemans and Klok, 2004). Furthermore, the precipitation on Morteratsch is ultimately estimated from stations located in different valleys, even though the distance between the stations is not very large. These considerations suggest that the precipitation treatment is likely to be the largest source of uncertainty in the calculation of the net mass balance of Vadret da Morteratsch.

Results

Figure 5 shows the modeled mass balance compared to the stake observations over five balance years between 2001 and 2005. The agreement is best for the balance year 2003/04, with a RMSE of 0.43 mw.e. a^–1. The other three years have a somewhat larger RMSE between 0.53 and 1.07mw.e. a^–1. The largest discrepancies can be found in the lower part of the glacier, especially in the warmer years. This may be explained by simplifications in the albedo parameterization and in the parameterization of the long-wave and turbulent energy fluxes. In the model, the ice albedo remains constant during the ablation period. In reality, however, the bare glacier surface may be covered with dirt after a longer period without snowfall, which decreases the albedo and consequently increases the amount of energy absorbed by the surface. Also the parameterization of the longwave and turbulent fluxes may cause an underestimation of melt at lower altitudes because in the model these fluxes depend only on air temperature. For example, near the glacier snout the valley is rather narrow. Longwave radiation from the valley walls that heat up during the day is not included in the parameterization. Also the humidity profile above the glacier surface is not explicitly included in the calculation of the turbulent fluxes, mainly because such data are not available for the whole period from stations in the proximity of the glacier. Finally, part of the underestimation can also be explained by using a fixed surface elevation distribution valid for the year 1998. The lowest part of the glacier is known to be almost stagnant (hardly any horizontal flow), and the surface elevation therefore lowers by about the ablation rate of up to 10ma^–1. Between 1998 and 2005 one could expect a lowering of the glacier tongue by 50–60 m. Assuming a mass-balance gradient of 1mw.e. (100 m)^–1, this already explains an underestimation of around 0.5 mw.e. for the lowest ablation stake by the end of the calibration period.

The model also does not capture the full effect of the shading. This can be clearly seen, for example, in 2003/04 and 2004/05 for the highest measurements on Vadret da Morteratsch along the cross-profile at 2550ma.s.l. and for the stake at 2650ma.s.l. on Vadret Pers. Here, the model shows less contrast than the observations. However, we also note that a fraction of the mismatches between model and observations is likely due to the inherent variability in the measurements from the random stake position.

Finally we used the model to reconstruct the mean annual balance of the whole glacier (specific mass balance) for the period 1865–2005 using the long climate records from Samedan and Segl Maria. To do this properly, it is important to take into account the major effect of the change of glacier geometry over this period. Since 1865 the glacier lost more than 2 km of its tongue, concomitant with a thinning at the snout of up to 200 m. We addressed this problem by first running the mass-balance model for both end members of the glacier’s size and elevation. The recent glacier geometry corresponds to the year 1998 as provided directly by the DEM of the Bundesamt für Landestopographie, Switzerland. Additionally, we reconstructed the 1865 glacier geometry from the known maximum extent of the glacier (Glaciological reports, 1881–2007; Reference Machguth, Paul, Hoelzle and HaeberliMaisch and others, 1999) and the height of the trimlines in the ablation area as inferred from the topographical map. We have no data that support significant geometry changes in the accumulation area of the glacier. The area–elevation distribution for both geometries is shown in Figure 6. If we assume that the retreat of the glacier was regular, and the length record indeed suggests an approximately linear retreat, then the actual specific mass balance between 1865 and 2005 can to a good approximation be found by a gradual linear interpolation between the specific mass-balance simulations for the two glacier geometries between 1865 and 1998, and a further linear extrapolation for the period up to 2005. Both curves for the simulated specific mass balance for the two geometries broadly show the same behaviour, with a mean difference of 0.27mw.e. Years with a more negative specific mass balance show slightly larger deviations, which can be explained by the larger ablation area in geometry1865 and the non-linear dependence of the melting on elevation (higher temperatures cause higher melting and a shorter period with snow cover). The interpolated specific mass balance is shown in Figure 7a. Nevertheless, the cumulative mass balances for geometry1865 and geometry1998 show quite large differences (Fig. 7b). While the cumulative mass balance is negative from 1865 onwards with geometry1865, it is around zero for geometry1998 until approximately 1920. At the end of the reconstruction period the cumulative mass balance for geometry1998 is –28mw.e. and for geometry1865 it is –67mw.e. A gradual linear interpolation/extrapolation between the two results gives a cumulative specific mass balance of –46mw.e., or a mean glacier thinning of about 51 m ice equivalent between 1865 and 2005. Incidentally, this mass loss is in very good agreement with the volume change divided by the mean glacier area of –44mw.e. inferred directly from the two geometries for the slightly shorter period 1865–1998.

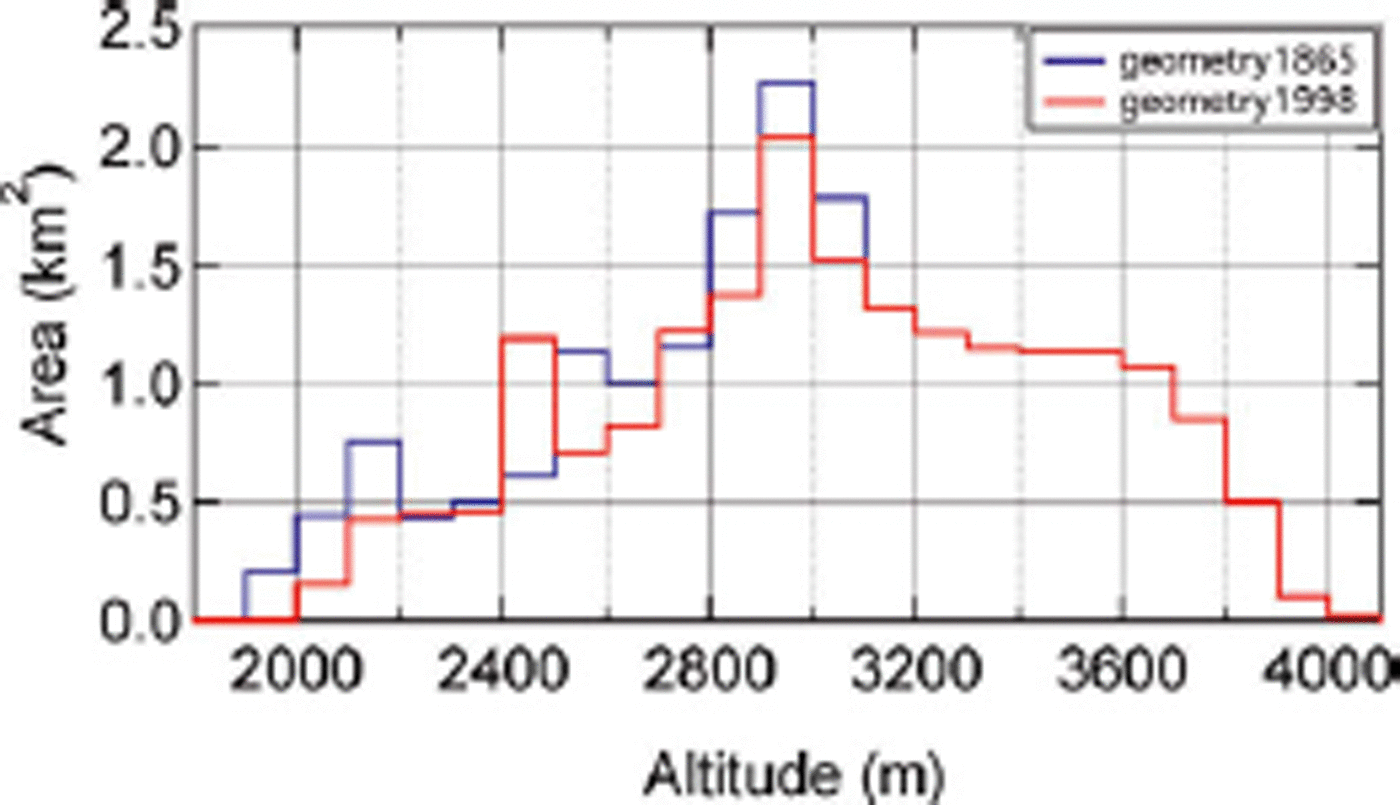
Fig. 6. Area–elevation distribution of Vadret da Morteratsch as adopted for the years 1865 (blue) and 1998 (red).

Fig. 7. (a) Interpolated annual mass balances for the period 1865–2005; (b) cumulative mass balance (with geometry1998, geometry1865 and interpolated) for the period 1865–2005.

In most of the years the interpolated specific mass balance is negative; only in 25% of the years (35 out of 141) was it positive. A trend towards a more negative mass balance can also be observed in the last two decades, starting approximately in 1980. Between 1970 and 1980, several years even had a positive specific mass balance. Before this period, the specific mass balance is negative in almost every year back to 1920, with a period of increased mass loss between 1940 and 1950. The cumulative mass balance shows only a few periods with a rising trend, most importantly between 1911 and 1920 when the glacier gained about 2mw.e. During the last 25 years of the simulation, the cumulative mass balance was –16mw.e., which represents 33% of the total mass loss of the last 141 years.

Similar features were obtained for other Alpine glaciers. For the period 1935–77, our results have a correlation coefficient of 0.88 with Aletschgletscher and 0.75 with Hintereisferner, for which specific mass balances were calculated with the hydrological method (Reference Schöner and BöhmSteinacker, 1979). For all three glaciers, the most negative mass balances during this period occurred between 1940 and 1950. In a recent publication, the mass balances of Aletsch, Rhone, Gries and Silvretta glaciers were reconstructed for the period 1865–2006 using a temperature-index model (Reference HockHuss and others, 2008). The results show regional differences between the four glaciers, but the pattern of ice loss is very similar to ours, with two periods of zero or slightly positive mass balance (1912–20 and 1974–81) and two periods with enhanced mass loss (1942–50 and 1998–2006).

Conclusions

The reconstructed mass loss of Vadret da Morteratsch between 1865 and 2005 is found to be approximately 46mw.e. This value is in good agreement with the volume change of 44 m inferred from the glacier geometries used for the reconstruction. The cumulative specific mass balance over this period shows an almost continuous mass loss, with short periods of mass gain around 1920, 1935 and 1980. After 1980 a trend towards a more negative mass balance is found. The decreasing specific mass balance is mainly associated with increasing summer temperature. A slight trend towards less precipitation can, however, be observed during the last 10 years. This trend is more obvious in the snow accumulation since snow accumulation decreases when temperature increases. In addition, the high annual variability in the specific balance appears most influenced by snow accumulation.

The comparison between the measured and the calculated annual balance shows a relatively good agreement. The largest discrepancies can be found in the lowest part of the glacier. The reason for this is the use of constant 1998 geometry and simplifications in the parameterization of the longwave and turbulent energy fluxes that in the model depend only on the air temperature. As especially the latent turbulent heat flux depends to a large extent on the humidity content of the air above the glacier surface, including the humidity could make a great improvement. This could be done, for example, by replacing the air temperature (Equation (2)) by the wet-bulb temperature or by the equivalent potential temperature (the temperature a parcel of air would reach if all the water vapour in the parcel were to condense, releasing its latent heat, and the parcel was brought adiabatically to a pressure of 1000 hPa), which both include humidity. Finally, we would like to point out that even though the glacier model provides a realistic output compared to mass balances of other glaciers as well as compared to the measurements, many aspects can still be improved. However, the model already seems capable of long-term calculations of mass balance as well as of driving a glaciological flow model to reconstruct the ice dynamics of the glacier retreat.