1. Introduction
For the development of natural resources in regions where sea ice is present, such as in the sea of okhotsk and arctic ocean, it is important to understand how waves propagate in ice-covered seas. the wave characteristics provide a means of estimating wave power, the ice impact force, composite forces that define the safe operation of ships and design loads for coastal structures, the prediction of oil-diffusion effects, and so on. the shape and number of ice floes have a considerable influence on the wave characteristics. Reference Sakai and HanaiSquire and dixon (2000) developed an analytic model for wave propagation across a crack in an ice sheet, and report that the reflection and transmission coefficients depend strongly on wave period.
Often field observations lack information on the ice conditions because of the difficulty of making such measurements. tank experiments are also hard to set up for arbitrarily specified ice conditions. the observations and the experiments are costly, take considerable time and are labour-intensive. on the other hand, if the wave characteristics in the ice-covered sea can be analyzed using a computer simulation, this will be a very effective means of alleviating the problems mentioned above.
In this study, a numerical method is reported based upon a time-domain solution incorporating the boundary element method (bem) and the finite-element method (fem) proposed by Reference Liu and SakaiLiu and sakai (2002). bem is applied to evaluate the water surface elevation, and fem is used to analyze the elastic deformation of the ice floe. indices are set up relating to the discrete nodes to distinguish the dynamic boundary conditions. to verify the accuracy of the method, the experimental data of Reference Ohyama and NadaokaSakai and hanai (2002) are used to compare with the numerical results. in addition, a computer simulation assimilating the sea-ice conditions of the southern part of the sea of okhotsk is tried.
2. Numerical Analysis
This numerical method defines a two-dimensional water tank of fluid domain Ω, as illustrated in figure 1. bem is applied to the fluid motion, and the fem is used to analyze ice-floe deformation. the wave–ice-floe interaction is simulated by prescribing the conditions on the wave generation boundary for each time-step and by satisfying continuity of pressure and displacement at the fluid–ice interface. waves generated by the wave generator Γ1 propagate in sea ice. after the waves decay on the sponge layer Γ2, they permeate the open boundary Γ3. although the ice floes are free to move vertically, they cannot collide with one another. it is assumed that the ice floe cannot separate from the fluid surface.

Fig. 1. Computation domain and the definition of the boundary conditions.
When the fluid is taken to be incompressible and inviscid and the flow is irrotational, the continuity equation in the fluid domain Ω can be expressed as laplace’s equation for a velocity potential δ:
For the two-dimensional problem, the ice floe is analyzed as a plate with unit width, and its equilibrium equation in the fluid motion is expressed by means of elastic bending theory:
Where ![]() is the flexural rigidity, E
i is the elastic modulus, h
i is the thickness, is poisson’s ratio, m
i is the mass, η is the displacement of the ice floe, and p is the pressure. the subscript i denotes the ice floe. the waves are generated by prescribing the water surface elevation,
is the flexural rigidity, E
i is the elastic modulus, h
i is the thickness, is poisson’s ratio, m
i is the mass, η is the displacement of the ice floe, and p is the pressure. the subscript i denotes the ice floe. the waves are generated by prescribing the water surface elevation, ![]() and by giving the horizontal velocity, ū(z), on the wave generation boundary, Γ1:
and by giving the horizontal velocity, ū(z), on the wave generation boundary, Γ1:
The bottom boundary, Γb, is taken to be impermeable, i.e.
Kinematic and dynamic boundary conditions are prescribed on the free water surface, Γf, and the fluid–ice interface, Γi, as follows:
Where s is the tangential vector on the boundaries, ϴ is the internal angle between the vertical direction z and the normal vector n, g is the acceleration of gravity, and ρ is the density of fluid. to attenuate the short-period waves, a numerical wave filter proposed by Reference Ohyama and NadaokaOhyama and nadaoka (1991) is set up at the end of the wave tank, which acts as a sponge layer Γ2:
=0 on Γ2.
The usual sommerfeld radiation condition is applied to the open boundary as the wave filter Γ3, to absorb long-period waves propagating through the wave filter Γ2. the boundary condition Γ3 is finally derived as the following equation:
Where μ in equations (9) and (10) is an attenuation coefficient that is linearly distributed and proportional to x.
Using a green’s function, equation (1) can be expressed as a boundary integral equation and solved using bem by dividing the whole boundary Γ into discrete nodes. by substituting the kinematic boundary conditions (4), (5), (6) and (10) into the boundary integral equation, the velocity potential, δ, of discrete nodes on the whole boundary Γ and the elevation, η, of discrete nodes on the boundaries of Γf, Γi and Γ2 can be determined by solving the dynamic boundary conditions (7–9). furthermore, when the vertical movement and the rotation of the ice floe are considered as the displacement of the node, and the shear force and the bending moment of the ice floe are considered as the external force, it is possible to solve equation (8) by using fem. the time-dependent variables, i.e. the velocity potentials, δ, on the Γ and the displacements, η, on the water surface and fluid–ice interface, are calculated with a constant time interval, Δt, by using a newmark-integration method.
Indices are set up to distinguish the boundary condition at discrete nodes. since the indices for the ice floes have information on the length, l i, thickness, h i, and the elastic modulus, E i, of the ice floe, it is possible to set arbitrary ice conditions easily and to simulate the characteristics of the wave under the ice floes. for instance, the indices for the free surface boundary condition, Γf, are set to zero, and the indices for the ice-floe boundary condition are set from 1 to 3 corresponding to the respective ice plates, as illustrated in figure 2. this distinction index for the dynamic boundary conditions is installed onto the discrete nodes as the input condition in the simulation.

Fig. 2. Definition of the distinction index for the dynamic boundary conditions: the indices for the free surface are zero and for the ice floes are 1 to n, where n is the number of floes in the computational domain.
3. Verification for Numerical Analysis
3.1. Experiments for verification
We carried out experiments in the wave tank to verify the accuracy of results obtained by the numerical analysis. the wave tank was 26m long, 0.8m wide and 1 m deep, as illustrated in figure 3. the water depth in the tank was 600 mm. wave generators, which incorporate a system to decrease the influence of wave reflection, were installed on both ends of the tank. model ice was floated for 8m at its center. as the elastic deformation of ice floes is the main purpose of our study, the horizontal movement of the model ice was restrained by steel pipes. wave profiles in the open water at the front and rear of the model ice were measured by two wave gauges, respectively. vertical displacements of the model ice were measured at 25 points along the center of the tank using an array of ultrasonic sensors.

Fig. 3. The wave tank and experimental equipment.
The experiments were conducted for three different sets of ice conditions. in cases 1 and 2 the ice sheet was of uniform thickness, while in case 3 it was non-uniform. the parameters of the ice sheet are shown in table 1. in cases 1 and 2, polyethylene sheet was used as the model ice. the
Table 1. Model ice conditions
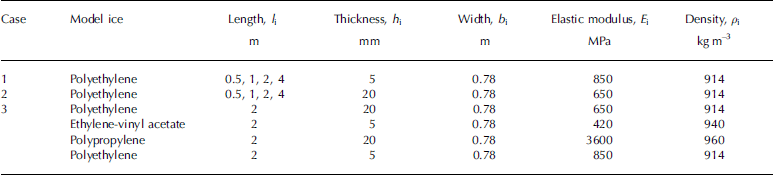
Thickness of the sheets was 5 and 20 mm, and the elastic moduli were respectively 850 and 650 mpa. the density of the polyethylene was 914 kgm–3 for both sheets. the length of the sheets was 0.5, 1.0, 2.0 or 4.0 m, and the number used was 16, 8, 4 and 2 respectively. regular waves of period 1.0–1.6 s were incident on the model ice, with the wave steepness being varied from 0.005 to 0.015. in case 3, polyethylene, polypropylene and ethylene-vinyl acetate were used as the model ice. four sheets of 2 m long polyethylene, ethylene-vinyl acetate, polypropylene and polyethylene, respectively of thickness 20, 5, 20 and 5 mm, and elastic moduli of 650, 420, 3600 and 850mpa, were set out from the top end of the tank. the density of the ethylene-vinyl acetate and the polypropylene was 940 and 960 kgm–3. the wave period was 1.4 s and wave steepness was 0.01.
3.2. Comparison of numerical results with experimental data
figure 4 shows comparisons of wave celerity below ice floes of 5mm thickness (case 1) between the numerical results and experimental data. the solid line indicates the wave celerity in open water. the horizontal axis is the distance from the tip of the ice floes. the wave celerity produced by the numerical analysis is almost consistent with that of the experimental data. figure 5 shows the same comparisons of wave celerity below ice floes of 20mm thickness (case 2). even though the ice floes are thick, the numerical results agree well with the experimental results. furthermore, figure 6 shows the mean velocity of wave celerity plotted in figures 4 and 5. the closed dots indicate case 1 (ice thickness 5 mm), and the open dots indicate case 2 (ice thickness 20 mm). it can be seen that the values computed by the numerical simulation correspond well with those of the experiments.

Fig. 4. Comparison of the wave celerity below the ice floes (case 1: thickness hi = 5 mm, length li = 0.5–4.0 m) between numerical results (open circles) and experimental data (closed circles) for the wave period T from 1.0 to 1.6 s.

Fig. 5. Same as Figure 4, but for case 2 (thickness hi = 20 mm, length li = 0.5–4.0 m).
figure 7 shows the temporal displacement of the four ice floes in case 3. in the figure, X i is the distance from the tip of the ice floes to the point of measurement. in the experiments, energy loss occurs due to friction between the water and the model ice plates. because friction is not included in the numerical analysis, the numerical predictions are slightly larger than the experimental data. in general, the numerical simulation provides a good explanation of the experimental phenomenon. the comparison of wave celerity in case 3 is shown in figure 8, where the values of the numerical simulation are again consistent with the experimental data. as a result, the method presented can be used to analyze the characteristics of wave propagation in sea ice.

Fig. 7. Comparisons of the temporal displacement of four ice plates (case 3: length li = 2 m for all plates, thickness hi = 20, 5, 20, 5 mm) between the numerical results (solid line) and experimental data (dashed line).

Fig. 8. Comparisons of the wave celerity below the four ice plates between the numerical results (closed circles) and experimental data (open circles) for case 3.
4. Numerical Analysis of Assumed Sea Ice in South Okhotsk
4.1. Calculation condition
We perform the numerical analysis based on the ice conditions observed in the southern sea of okhotsk. these are adapted from data measured in satellite images reported by Reference Squire and DixonTakatsuji (2004). figure 9 shows one example of a landsat 7 satellite image. figure 10 is the result obtained by image analysis and shows the relationship between the diameter and the cumulative number of ice floes. when the diameter of the ice floes is 100, 200, 400 m, the corresponding cumulative number is 4, 2, 1. the length of the ice floes was assumed here to be their diameter and was set to a scale of 1 : 100. the thickness of the ice floes was set to 20 and 40 mm because of the difficulty of measurement. the density and elastic modulus of the ice floes are respectively 914 kgm–3 and 650 mpa. ice floes were arranged at random. the calculation condition of ice floes is shown in table 2. a regular wave of 1.4 s period is used as the incident wave, with a steepness of 0.01.

Fig. 9. Image of ice floes captured by Landsat 7 satellite (Takatsuji, 2004).

Fig. 10. Relationship between the diameter and the cumulative number of ice floes, obtained by image analysis and presented by Reference Squire and DixonTakatsuji (2004).
Table 2. Ice-floe conditions determined by observation in the southern Sea of Okhotsk: l i is length, h i is thickness, E i is elastic modulus and ρ i is density
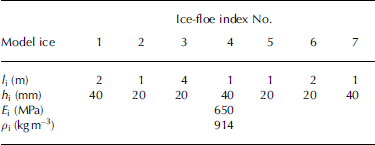
4.2. Calculation result
figure 11 shows the spatial profile of deformation, η, of ice floes at t = 10, 15, 20 and 25 s. the dashed line indicates the still water level. when the ice floes are long and thin, the deformation follows the wave closely. on the other hand, when they are short and thick, the deformation accompanies a substantial rigid body movement. it is expected that the deformation of each ice floe depends strongly on its flexural rigidity.
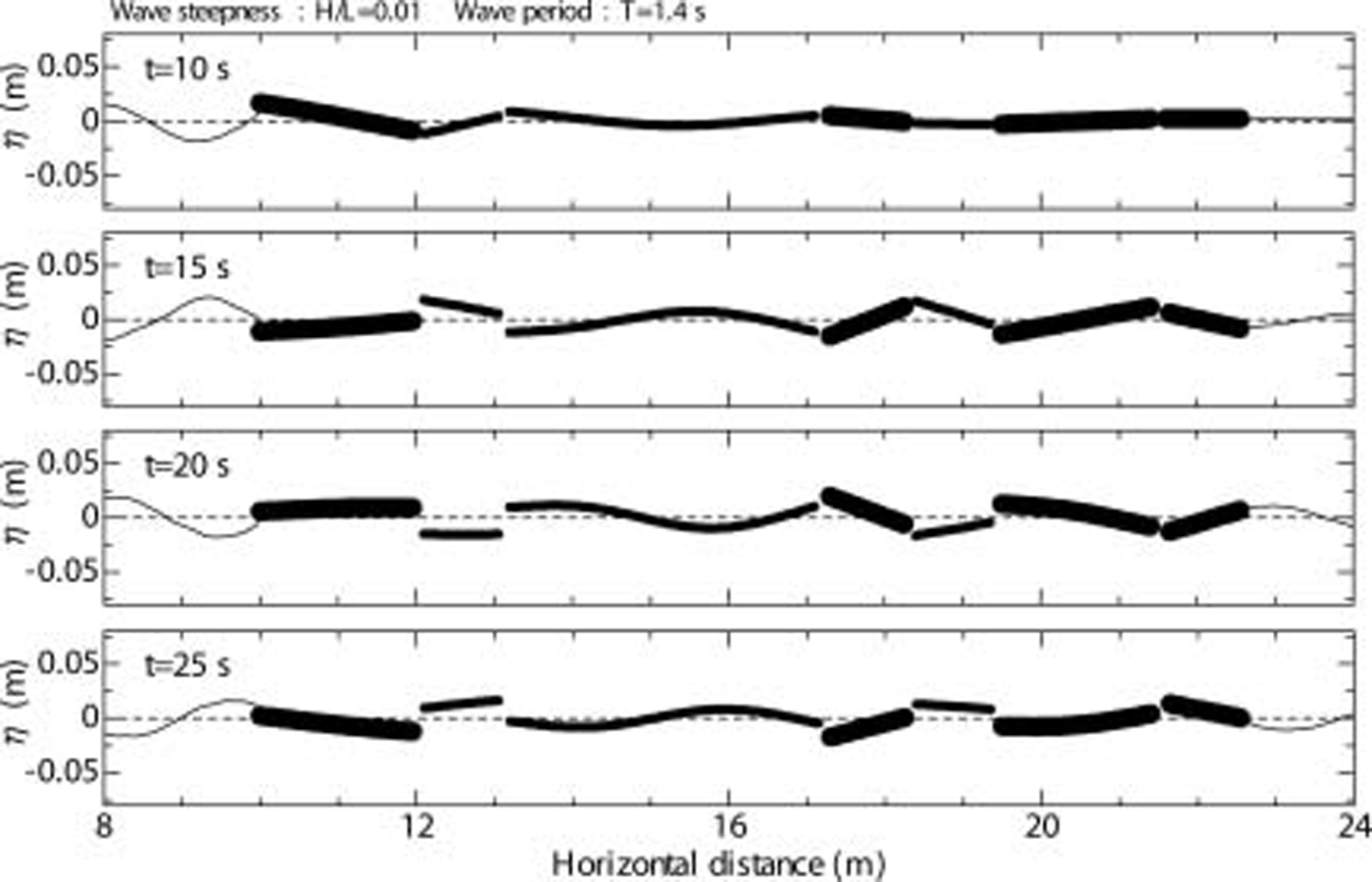
Fig. 11. Temporal changes of the spatial profile of ice-floe deformation at times t = 10, 15, 20 and 25 s, calculated for the sea ice of the southern Sea of Okhotsk.
5. Conclusions
Because the wave celerity below the ice floes and their temporal displacement, calculated by the numerical method, are consistent with the experimental data, it is argued that the method presented is valuable in the analysis of the characteristics of waves propagating in sea ice. in particular, it has been possible to simulate the properties of waves propagating in sea ice for a simple ice condition and for arbitrarily specified ice conditions, by passing the distinction index for the dynamic boundary conditions to the discrete nodes. further, it is clear that the length and the flexural rigidity of ice floes strongly influences their deformation during wave propagation.
















