Introduction
The metamorphism of snow is a thermo-mechanical process which occurs continuously once snow has been deposited on the ground. A large number of studies have been done on the various forms of snow metamorphism, including the significant works of de Quervain (Reference Quervain de1945, Reference Quervain de and Kingery1963), Reference Giddings and LaChapelleGiddings and LaChapelle (1962), Reference Yosida and KingeryYosida (1963), Reference Hobbs and MasonHobbs and Mason (1964), Reference Hobbs and RadkeHobbs and Radke (1967), Reference WakahamaWakahama (1968), Colbeck (Reference Colbeck1973, Reference Colbeck1979), Reference PerlaPerla (1978), Adams and Brown (Reference Adams and Brown1983, Reference Adams and Brown1989, Reference Adams and Brown1990), and Reference Adams and SatoAdams and Sato (1993).
One of the remaining questions has to do with our ability to predict the rates of change of the snow microstructure under any given set of conditions. Some of the work by previous investigators has attempted to do just this with varying degrees of success. Colbeck (Reference Colbeck1980) and Reference Maeno and EbinumaMaeno and Ebinuma (1983) have considered the rate of change of either grain-size or intergranular bonding. One of the difficulties in assessing the accuracy of any model is the difficulty associated with measuring the material microstructure. Snow usually has a very complicated microstructure with a wide variety of grain shapes and grain-sizes as well as a potentially high degree of anisotropy. With the advent of image analysis systems and new techniques of quantitative stereology (Reference Brown and EdensBrown and Edens, 1991; Reference Edens and BrownEdens and Brown, 1991, personal communication), this problem has to some extent been resolved.
The purpose of this study is the theoretical analysis of the rates at which radius-of-curvature metamorphism proceeds in dry snow. The results presented here, from a combined theoretical and laboratory experimental program, are preliminary, and work continues in an attempt more precisely to describe the thermo-mechanical processes responsible for radius-of-curvature metamorphism. Work is continuing also in measuring how the micro-structure of snow is altered during equitemperature conditions and to compare the measured changes with those that are predicted by the modeling. For this work we use “standard snow” (see Experimental Study) consisting of spherical particles with grain-sizes on the order of 20 to 200 μm.
Finally, we are also considering the application of mixture theory to this problem to determine if such an approach can be of use. The work described here will provide a means of assessing the utility of mixture theory for this type of metamorphism.
Analysis of radius-of-curvature metamorphism
In this section we consider the interchange of mass between two neighboring ice grains that are assumed to be spherical but have different radii of curvature. In such a situation, the equilibrium vapor pressures over the two surfaces will be different, therefore resulting in a vapor pressure gradient between the two ice grains. This in turn produces a flux of mass from the small grain to the larger one. Over a sufficient period of time this can result in a measurable alteration of mean grain-size and the statistical distribution of grain-sizes making up the material. Calculations here will provide information on just how quickly this process takes place.
Reference ColbeckColbeck (1980) indicated that a small relative change in temperature θ produces proportionately larger relative changes in vapor pressure Pv and vapor density ρv. Therefore the assumption of a constant temperature across a vapor space between two neighboring ice surfaces might impose too strong a restriction and produce potentially unrealistic estimates of vapor flux. As a consequence we make no assumptions concerning constant temperature. The governing balance equations are solved to obtain estimates of such variables as temperature, vapor pressure, vapor density, and vapor flux. The balance equations used are those of mass, momentum, and energy. These are used in conjunction with constitutive relations governing the behavior of the vapor phase.
Consider two neighboring ice surfaces separated by a small space containing an air/vapor mixture which under normal conditions is vapor saturated (Fig. 1). We assume one surface has a prescribed temperature and that initially both surfaces have given radii of curvature. The intent of this analysis is to determine the exchange of mass between the two surfaces when no macroscopic temperature gradient is imposed.

Fig. 1. Schematic of two grains exchanging mass in the absence of an imposed temperature gradient.
In what follows the subscripts “a” and “b” refer to the two ice surfaces, where the surface “a” is the one with the prescribed temperature. The subscripts “s” and “v” will refer to the solid and vapor phases respectively.
The well known Clausius–Clapeyron equation and the Kelvin relation may be used to develop a single expression for the equilibrium vapor pressure in terms of both temperature and surface curvature. The Clausius–Clapeyron equation gives the vapor pressure as a function of temperature:
where Ρ is the equilibrium vapor pressure, R is the gas constant, and L is the latent heat of sublimation. θ0 is a reference temperature, and PR a reference pressure for vapor over a surface at the reference temperature. The vapor pressure in terms of the mean radius of curvature, r, is given by the Kelvin equation:
P0 is the saturation vapor pressure at the reference temperature θ0. The surface energy is denoted by σ.
Assuming the reference temperature in the two equations are the same, the above two equations can be combined to yield:
where α and β have the values of 2σ/ρsRθ0) and Ls/R, respectively. It is usual to choose either the triple point or the melting point as the reference temperature. The radius of curvature of an ice surface, r, is determined by the two values r1 and r2 which are the radii of curvature of the surface in two orthogonal directions (Reference HobbsHobbs, 1974). It is given by the relation:
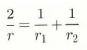
Finally the mass and heat balance equations are given by:
In the above q is the mass flux, and Q is the heat flux, and ρv is the vapor mass density. The terms D and A represent the binary diffusion coefficient and the cross-sectional area over which the transfers are taking place. k is the thermal conductivity. It is assumed that the areas for the mass and heat flux are the same. We assume the heat flux is approximated by:
i.e. the heat transfer is predominantly due to the transport of the latent heat of sublimation Lss. Equations (5)–(7) can be combined to yield:

k and D are both weak functions of temperature and are determined by the relations:

In Equation (9) Ρ is the total air and vapor pressure, and ka is the air conductivity and has the constant value of 0.024 W m−1 K−1). Since variations in temperature are expected to be very small, D and k will be treated as constants. Then the integration of Equation (8) yields:
Substituting the ideal gas law, we obtain:
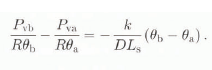
Rearranging gives:
where:

At point b (see Fig. 1), Equation (3) can be written as:
where

We can combine Equations (12) and (14) to obtain a relation for θb that can be solved by an iterative procedure:

Once θb is found, the vapor pressure at point a and b can be found with Equation (3), after which the vapor densities ρva and ρvb can be found with the ideal gas law.
Once the pressures, temperatures and densities are found at points a and b, the mass flux q across the vapor space from surface a to surface b can be found with the use of Equation (5). The area A is taken to be the projected cross sectional area of grain a, A = πra 2, where the grain a is assumed to be the smaller of the two grains. Assuming a separation distance ΔL, the mass flux can be approximated with the use of Equation (5) by letting:

The rate of change of grain-size is then:

where ρice is the density of ice. Deposition on grain b and sublimation olf grain a will not be uniformly distributed over the respective grain surfaces, so these calculations give rates of change of effective grain-sizes. However, these measurements are essentially what is measured by most image analysis systems, i.e. the equivalent spherical grain-size is determined.
Analysis of thermodynamic sintering
In the previous section we studied the processes which determine how ice grains of different radii of curvature exchange mass when temperature gradients are negligible. An additional process, which we refer to as thermodynamic sintering, also can take place at the same time. This involves the exchange of mass between the ice grains and the bonds or necks connecting the ice grains. The necks usually have radii of curvature substantially different from ice grains, so that the equilibrium vapor pressure over the neck surfaces will differ from that over the grain surfaces. This consequently produces a flux of vapor from the grain surface along the surface to the neck, where it is subsequently deposited on the neck surface. As a result the necks slowly grow with a resulting increase in the material strength and rigidity. In this section we attempt to calculate the rates at which this process proceeds and to determine if the deposition of mass is uniformly distributed on the neck surface.
We do not consider here mechanical sintering due to applied pressures or other loads to the snow. Rather we

Fig. 2. Schematic of neck/grain geometry for calculating flux of vapor mass from grain surface to neck surface. The relative sizes of grain and neck are not drawn to scale

Fig. 3. Schematics of control volume used for balance of momentum and mass for thermodynamic sintering
are interested in the growth of intergranular necks and bonds due to transfer of mass from grain surfaces to the bonds connecting the grains. Figure 2 illustrates the geometry of a grain connected to a neck. From this two-dimensional perspective, the radius of curvature changes from a positive value on the body of the ice grain to a negative value on the ice neck. In reality the neck radius of curvature may not be negative, since, as indicated in Equation (4), the value of r used in the following analysis must reflect the radii of curvature on two perpendicular directions. The curvature of the neck will however be lower than on the surface of the grain, and as a consequence the equilibrium vapor pressure over the neck surface will be lower than over the grain surface, and the vapor will move from the grain toward the neck. Here we develop the governing relations for this process by requiring that the principles of balance of mass, momentum and energy be satisfied. We assume the radius of curvature is a function of the distance x along the grain surface shown in Figure 2. Also shown in that figure is a small cell which we utilize to characterize the balance relations. These are shown in more detail in Figure 3.
The thickness, δ, of the cells is taken to be large enough so that the flux of mass across the top of the cell is small compared to fluxes across the two sides of the cell. There is some subjectivity to a proper choice of δ, but a choice of one-half the pore thickness would certainly represent an upper limit on acceptable values for δ.
First consider balance of mass, which is depicted in Figure 3a. This gives the following balance relation if we assume steady state:

In the above, ν is the vapor velocity, and ![]() is the mass supply, which represents the rate at which vapor is being formed by sublimation off the ice surface of the grain or neck. Balance of momentum using Figure 3(b) yields:
is the mass supply, which represents the rate at which vapor is being formed by sublimation off the ice surface of the grain or neck. Balance of momentum using Figure 3(b) yields:

In the above the resisting shear stress in the fluid has been assumed to be Newtonian and has been approximated by the term τ = (μ/2)∂ν/∂y = μ(ν/2δ). The term, μ, is the fluid viscosity, and the velocity gradient is approximated by a linear distribution across the boundary layer in which the vapor flow is taking place. The thickness δ of the boundary layer will be taken to be one-fourth of the mean pore size. Also in the above equation η is the drag coefficient for water vapor in air. This is closely related to the binary diffusion coefficient, D, used in the previous section. The binary diffusion coefficient is used in the application of Fick’s law as used in the previous section (Equation (5)). However, here we are using the momentum balance equation rather than a direct application of Fick’s law. In the momentum balance equation, the momentum interaction between the vapor and air in the pores is given by a drag coefficient, η, which when multiplied by the vapor velocity, gives a term with the same dimensions as the stress gradient, and the product η.ν represents the resistance of the air to the motion of the vapor.
Balance of energy can be readily found by considering the exchange of energy in each cell. We assume that energy transfer takes place by both conduction of heat and transfer of latent heat. We neglect the dissipation of energy due to the stress, since this is a second order term in the velocity gradients and is insignificant relative to the heat transfer. Balance of energy along the ice surface gives:

In the above k is the conductivity of the air/vapor phase. The unknown in this problem is the set (ν, θ ![]() , ρv, Pv). The equations for balance of mass, momentum and energy provide three relations, and Equation (3) and the ideal gas law allow us to close the problem, with the specification of the appropriate boundary conditions. These equations are coupled and nonlinear, so a numerical method will be used.
, ρv, Pv). The equations for balance of mass, momentum and energy provide three relations, and Equation (3) and the ideal gas law allow us to close the problem, with the specification of the appropriate boundary conditions. These equations are coupled and nonlinear, so a numerical method will be used.
Substitution of the ideal gas law and Equation (3) into Equation (21) gives:

where:
The solution will involve the following iterative procedure. Since Equation (22) contains only the temperature θ, velocity ν and the mass exchange rate, ![]() , it will be initially solved by assuming
, it will be initially solved by assuming ![]() and then solving for the temperature distribution. An iterative procedure can be used by first making an initial guess of the temperature distribution along the ice surface and then solving Equation (22) for an updated approximation. This updated temperature distribution is used as the next guess, and the procedure is solved again and this is continued until convergence is reached. This then gives a solution for the temperature distribution but with no diffusion velocity or sublimation.
and then solving for the temperature distribution. An iterative procedure can be used by first making an initial guess of the temperature distribution along the ice surface and then solving Equation (22) for an updated approximation. This updated temperature distribution is used as the next guess, and the procedure is solved again and this is continued until convergence is reached. This then gives a solution for the temperature distribution but with no diffusion velocity or sublimation.
With this solution Equations (3), (19), (20) and the ideabas law are used to obtain solutions for υ, ρv, Pv, and ![]() . In order to do this Equations (21) and (20) can be combined by first pre-multiplying Equation (19) by the velocity v and then using Equation (20) to eliminate the term ν ∂υ/∂x. This results with the equation:
. In order to do this Equations (21) and (20) can be combined by first pre-multiplying Equation (19) by the velocity v and then using Equation (20) to eliminate the term ν ∂υ/∂x. This results with the equation:

With the temperature distribution, the pressure profile ∂Pv/∂x can be found from Equation (3) and then used in Equation (24) to find the velocity profile of the vapor along the ice surface on the neck and grain. Once this is done, Equation (20) can be used to calculate the mass exchange rate ![]() . These solutions for
. These solutions for ![]() , ρv. Pv and ν are then used as second estimates in Equations (22) to find a second approximation for the temperature distribution θ, and the entire process is again repeated until convergence is reached. This iterative solution technique was found to be stable for this particular problem.
, ρv. Pv and ν are then used as second estimates in Equations (22) to find a second approximation for the temperature distribution θ, and the entire process is again repeated until convergence is reached. This iterative solution technique was found to be stable for this particular problem.
Results of theoretical analysis
In the following we consider the effect of a number of parameters on the rate of mass exchange between two grains, one small and the other large. We denote the small grain as grain a and the large as grain b. Figure 1 illustrates the geometry of the two grains.
Temperature would be expected to have a very significant effect on the rate at which the two grains would exchange mass. As the temperature is decreased, the saturation vapor pressure and vapor density also decrease, thereby affecting the rate at which mass can be transferred from one grain to the other. To demonstrate

Fig. 4. Effect of temperature on rate of change of grain radius. Grain a initial radius 0.01 mm, grain b 1.0 mm

Fig. 5. Variation of grain-size as affected by size of grain a. Grain b has a radius of 1.0 mm

Fig. 6. Effect of grain b radius on rate of decrease of grain a size.

Fig. 7. Effect of separation distance ΔLon the rate of mass transfer between ice grains.
this, two temperatures were used in solving the equations developed in the previous section. These are shown in Figure 4. Since the experiments involved snow particles with diameters of approximately 0.020 mm, the initial size of grain a was also taken to be this size. Grain b had a size 100 times larger than grain a and therefore appears for all practical purposes to be a flat surface. This will be discussed shortly in more detail. As can be seen in Figure 4, approximately 1000 d are required for the small grain

Fig. 8. Vapor deposition rates along a grain surface due to movement of vapor from the grain surface toward the neck. The coordinate position x = 16 µm marks the change in surface curvature as the grain surface is left and the neck surface is entered. Case A is when there is a sharp change in curvature. For Case Β the radius changes gradually from 10 μm to 20 μm over a distance of 10 μm.

Fig. 9. Distribution of vapor velocity along grain surface and neck surface for two cases. For Case A the radius of curvature jumps from 10 μm to 20 μm at the point x = 16μm in the figure. For Case Β the radius changes gradually from 10 mm to 20 mm over a distance of 10 mm
to be reduced to 10% of its original diameter at the lower temperature, while about 650 d are required at 268 Κ. One can readily see that this form of metamorphism is a very slow process.
Grain-size also has an effect on the rate of metamorphism. The equilibrium vapor pressure is increased at an ice/vapor surface as the radius of curvature is decreased. Figure 5 illustrates the effect of grain a radius on the rate of mass transfer. By the time the grain a has been increased to a value of 0.1 mm it requires on the order of 150 years to be reduced to 10% of its original radius. This is due to the vapor pressure being reduced by increasing curvature and to the increased mass involved as the radius is increased. In fact, this latter effect is probably the dominant effect in this case, since the mass increases with the cube of the grain radius.
The relative size of the two grains will also have a significant effect on the rates involved. In this case we keep the grain a radius ![]() constant at a value of 0.01 mm and vary the grain b radius
constant at a value of 0.01 mm and vary the grain b radius ![]() between 0.01 mm and 10 mm, so that the ratio
between 0.01 mm and 10 mm, so that the ratio ![]() varies between 1 and 1000. Figure 6 shows the time required for the small grain to be reduced to 10% of its initial value. As expected, as the ratio
varies between 1 and 1000. Figure 6 shows the time required for the small grain to be reduced to 10% of its initial value. As expected, as the ratio ![]() approaches unity, the time required to accomplish this reduction goes to infinity. However the time required also approaches a constant value by ihe time the radius ratio reaches a value of
approaches unity, the time required to accomplish this reduction goes to infinity. However the time required also approaches a constant value by ihe time the radius ratio reaches a value of ![]() . After that, the grain b appears much like a flat surface.
. After that, the grain b appears much like a flat surface.
Finally, Figure 7 demonstrates that the separation distance between particles also has a definite effect on the rate of transfer of mass between particles. In this case ΔL is varied from a value of 0.01 mm to 0.05 mm. As the distance is shortened, the rate of transfer increases markedly as the vapor pressure gradient increases.
Figures 8 and 9 demonstrate the solutions to the equations describing the sintering process discussed earlier. Results are not shown for the temperature profile, since temperature variations using Equation (22) were very small. These last two figures show results of calculations for two different cases. Case A describes the situation where a sharp jump in surface curvature occurs, whereas Case Β is for the gradual transition from one radius of curvature to a larger curvature in the necked region. The reason for considering these two cases rests with what will actually occur when snow is first formed, either by snow deposition during snowfall or by the formation of snow with a processing technique.
When two ice grains first come into contact with each other, the region of contact will be a surface with a sharp change in surface curvature. This very localized region should experience a fairly rapid exchange of mass between the surfaces on opposite sides of the contact point. However as time passes, the sublimation and deposition of mass taking place during this exchange of mass will result in a region of surface with a gradually changing surface curvature, and hence the details of the mass exchange between the surfaces on either side of the original contact point should gradually change. These two cases were evaluated to determine the nature of the transport of mass from the ice grain to the neck, first when the transition is sharp and second for the situation after the surface has been smoothed. Work is continuing to calculate the temporal change in the shape and curvature of the necked region between the two grains, and what is reported here represents our first attempt at studying this problem.
As can be seen in Figure 8, for the case with a sharp jump in curvature between the grain body and neck, most of the mass exchange takes place right at the transition. For the second case, the mass transfer is spread out over the region of the transition. Figure 9 shows the corresponding vapor diffusion velocities, where similar results are obtained. One can see that the spatial distribution of both the vapor velocity and the vapor deposition is not symmetrically distributed as one progresses along the ice surface from the grain on to the neck. Rather, at a sharp transition in curvature, the sublimation/deposition process is very local, and as the ice surface shape gradually changes, this process slowly becomes more uniformly distributed. However, the flow velocity and sublimation/deposition is not symmetrically distributed along the surface. Since the surface geometry is not symmetrical, this should not be surprising.
The results of this last set of calculations demonstrates that the sublimation/deposition and vapor flow is strongly affected by the surface geometry. As a consequence, the neck cannot be expected to develop uniformly across its full length, although as time passes it appears that the process tends to smooth put
Experimental study
In order to make the experimental investigation as easy as possible, we use “standard snow” consisting of spherical particles, rather than the complicated grain shapes usually found in natural snow. This snow is made by a new instrument recently developed in Japan under the sponsorship of the Japan Science and Technology Agency; the machine produces spherical snow particles in considerable quantity, so that large samples can be studied — more than were available to previous investigators (Reference Hobbs and RadkeHobbs and Radke, 1967).
Standard snow can be made with mean grain sizes from 20 to 200μ in diameter. This study considers standard snow with initial grain size about 20 μ, chosen because the metamorphism proceeds much more quickly in fine-grained snow than in coarser snow. Radius of curvature effects become very significant at these small grain-sizes, and the process can be observed more quickly.
A nozzle forces water droplets of a diameter about 20 μ into a tube with walls of dry ice. The droplets quickly freeze on their outer surfaces, and are deposited in small containers measuring approximately 20 mm × 20 mm × 10 mm. As the aging process starts immediately, one

Fig. 10. Digitized surface sections of model snow samples showing the evolution of grain-size and intergranular bonding with time under equilibrium conditions

Fig. 11. Distribution of grain-size areas in surface sections for the four times shown. This figure shows the fraction of grains having a given cross-sectional area in the surface section plane
sample was filled with aniline solution and frozen at –20°C, representing time t = 0. Other samples, stored at –5°C in a sealed container packed with snow (to guarantee a vapor-saturated environment) were removed and filled with aniline solution at times of 30 min, 1 h, 2 h, 6 h, 12 h, 1 d, 3 d, 1 wk, 2 wk. 1 mnth and 2 ninth, and frozen at –20°C to stop metamorphism. The samples were then used to make surface sections to analyze the microstructure.
Surface sections were made by using water blue powder to stain the ice particles that were exposed on the section surface. Figure 10 shows two typical surface sections. As can be seen, the particles have a predominantly spherical shape, and the existence of bonds with adjoining necks can clearly be seen. The simple geometry of the spherical particles makes it easier to identify ihe necks and their dimensions. A stereological method used to determine the microstructure was essentially that of Edens and Brown (personal communication).
One of the purposes of this study was to determine how grains grew with time. Figure 10, showing surface sections for times of t = 0 and 72 h, indicates an increase in mean grain-size, and bonding between the grains has also developed.
Figure 11 illustrates the distribution of grain-sizes for times of 0 and 72 h. It shows the surface area of the grains exposed in the surface section plane, but not the distribution of grain-size volumes. It does not translate directly into grain-volume distributions, but shows that the microstructure is acquiring a more uniform grain-size distribution with time.
Conclusions
This study was undertaken to determine details of radius-of-curvature metamorphism. Physical models were formulated to calculate the movement of vapor and mass between ice grains and from ice-grain surfaces to the bonds connecting the grains. Results show that the microstructure of ihe material changes slowly with time. Small grains slowly lose mass to larger grains, at rates that are affected by pore size, relative size of ice grains and temperature. It is also possible that statistical distribution of the grain-sizes also has an effect, but this study was not able to verify this possibility. Calculations showed that the process of sintering takes place at a slow rate. The movements of vapor along the grain surface to the neck surface is not a uniformly distributed process. Rather it is determined by the details of the surface curvature of the grain and neck. More work needs to be done to determine the temporal evolution of the grain/neck geometry during the sintering process. This process is assumed to be due primarily to the sublimation of vapor off the ice-grain surface, diffusive transportation along the grain surface to the neck and subsequent deposition onto the neck. The rate of this process will change markedly as the surface geometry is modified over time.
Acknowledgement
This work was funded by the Army Research Office under (Grant No. DALE 03-92-G-0310) and the Japan Science and Technology Agency, to which the authors wish to express their appreciation.













