1. Introduction
The relationship between glacier sliding speed and the shear stress at glacier beds has been a major uncertainty in efforts to model glacier flow for over 60 years (Weertman, Reference Weertman1957). More recently, as interest in ice-sheet response to climate warming has mounted, modeling studies have highlighted the sensitivity of ice loss and sea-level rise projections to the form of the sliding rule (Ritz and others, Reference Ritz2015; Tsai and others, Reference Tsai, Stewart and Thompson2015; Brondex and others, Reference Brondex, Gagliardini, Gillet-Chaulet and Durand2017; Joughin and others, Reference Joughin, Smith and Schoof2019).
Of many proposed sliding rules, none has greater potential for contributing to fast glacier flow than the one first advocated by Lliboutry (Reference Lliboutry1965, Reference Lliboutry1968, Reference Lliboutry1979) in which ice can separate from the lee surfaces of sinusoidal bed undulations. In this case, neglecting regelation, the shear stress increases with steady sliding speed, reaches a maximum, and then decreases over a commonly wide range of sliding speed. This decrease in stress with increasing speed, which we call rate-weakening drag, results from lee side cavities that increase their size with increasing speed; thus, with increasing speed, diminished zones of ice–bed contact on convex bumps are inclined up-glacier at smaller angles, decreasing drag. This model is conceptually in accord with the upper bound on basal shear stress described by Iken (Reference Iken1981) that depends on the maximum adverse slopes of bumps on the bed and effective pressure. Subsequent analyses of sliding with ice–bed separation have been more self-consistent and less heuristic (Fowler, Reference Fowler1986, Reference Fowler1987) and have considered more complicated bed undulations (Schoof, Reference Schoof2005; Gagliardini and others, Reference Gagliardini, Cohen, Råback and Zwinger2007). These analyses qualitatively affirm the peak in shear stress and rate weakening of Lliboutry's (Reference Lliboutry1968) theory. Moreover, results of laboratory ring-shear experiments with sinusoidal beds demonstrate rate-weakening drag and agree quantitatively with Lliboutry's analysis (Zoet and Iverson, Reference Zoet and Iverson2015).
However, whether rate-weakening drag associated with cavity growth occurs at glacier beds over length scales large enough to be significant is unknown. Field observations of deglaciated bedrock demonstrate unequivocally that cavities are ubiquitous on hard beds (Walder and Hallet, Reference Walder and Hallet1979; Hallet and Anderson, Reference Hallet and Anderson1980). However, Fowler (Reference Fowler1987) and Lliboutry (Reference Lliboutry1987) thought that large bumps on glacier beds not submerged in cavities would prevent rate-weakening drag. Although Schoof (Reference Schoof2005) demonstrated that this viewpoint was not necessarily true, he nevertheless advocated a simpler sliding rule in which shear stress, normalized by effective pressure, asymptotically approaches an upper bound without rate weakening.
One motivation for disregarding the rate-weakening drag of sliding theories may come from debris entrained in the basal ice of glaciers. Friction between this debris and the bed contributes to basal shear stress and depends on particle–bed contact forces. In models of debris-bed friction with no ice–bed separation (Hallet, Reference Hallet1981; Shoemaker, Reference Shoemaker1988), particle–bed contact forces depend on the rate of ice convergence with up-glacier facing (stoss) surfaces during sliding. The resultant component of ice flow toward the bed past particles causes a pressure gradient across them with an associated drag that pushes them against the bed, increasing friction and hence basal shear stress. Ice convergence with surfaces facing up-glacier also occurs when leeward cavities persist at the bed (Iken, Reference Iken1981). For increasing sliding speeds and cavity sizes, rates of ice convergence and contact forces increase. This increase results from enhanced rates of basal melting and bed-parallel ice extension, caused by increasing normal stresses over diminished zones of ice–bed contact.
This effect motivates the hypothesis we wish to test: that higher particle bed-contact forces at higher slip velocities may lessen or eliminate the rate-weakening drag of sliding models with ice–bed separation (e.g. Lliboutry, Reference Lliboutry1968; Fowler, Reference Fowler1986). We combine existing theories of clean-ice sliding and of debris-bed friction without ice–bed separation to estimate total basal shear stress as a function of sliding speed. We find that debris-bed friction does not eliminate or significantly reduce rate-weakening drag.
2. Clean ice
In sliding theories, no shear traction acts locally at the bed surface, owing to the water film that divides wet-based glaciers from their beds. Ideally, a local shear traction commensurate with debris-bed friction could be included in such models so that stresses, ice flow and cavity sizes could reflect that friction. Although aspects of this problem have been studied with the finite-element method (Schweizer and Iken, Reference Schweizer and Iken1992), no analytical model exists that includes local shear tractions and ice–bed separation. Therefore, our tactic is to investigate what insights are possible using existing sliding theory to estimate debris-bed friction, neglecting its feedback on ice flow – a reasonable assumption if shear stress from debris-bed friction is a small fraction of the total basal shear stress.
To analyze sliding with ice–bed separation, we use the theory of Lliboutry (Reference Lliboutry1968) because it enables, in an approximate way, use of a Glen-type, non-linear ice rheology, and because aspects of the theory have been tested experimentally (Zoet and Iverson, Reference Zoet and Iverson2015). Like most other sliding theories that include ice–bed separation, the theory neglects regelation. This simplification is justifiable because on stoss surfaces where ice is in contact with rock, glacial abrasion generally smooths surfaces (e.g. Hooke, Reference Hooke2005), causing roughness elements as small as the controlling obstacle size (e.g. Weertman, Reference Weertman1957) to be relatively rare. Slip velocity is imposed as an independent variable in the far-field above bumps. No shear traction is allowed locally on the bed surface, owing to the water film, as noted, and the shear traction between water in cavities and cavity roofs is negligibly small. All drag therefore, for the case of clean ice, stems from the distribution of normal stress on the glacier sole exerted by rock in zones of ice–bed contact and by water under pressure in lee side cavities.
Lliboutry (Reference Lliboutry1968) considered a 2-D, rigid bed with a longitudinal profile,
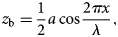
where x is measured parallel to average slope of the bed, a is the bump height from trough to crest, and λ is the wavelength (Fig. 1a). The roughness is ${\rm {\cal R}}$ = a/λ. Making various approximations, Lliboutry used the bump geometry, slip velocity u, effective pressure, N and the ice flow law parameters to estimate the cavity length, L c (Fig. 2):
= a/λ. Making various approximations, Lliboutry used the bump geometry, slip velocity u, effective pressure, N and the ice flow law parameters to estimate the cavity length, L c (Fig. 2):

where s is the fraction of the bed in contact with ice:
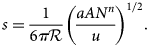
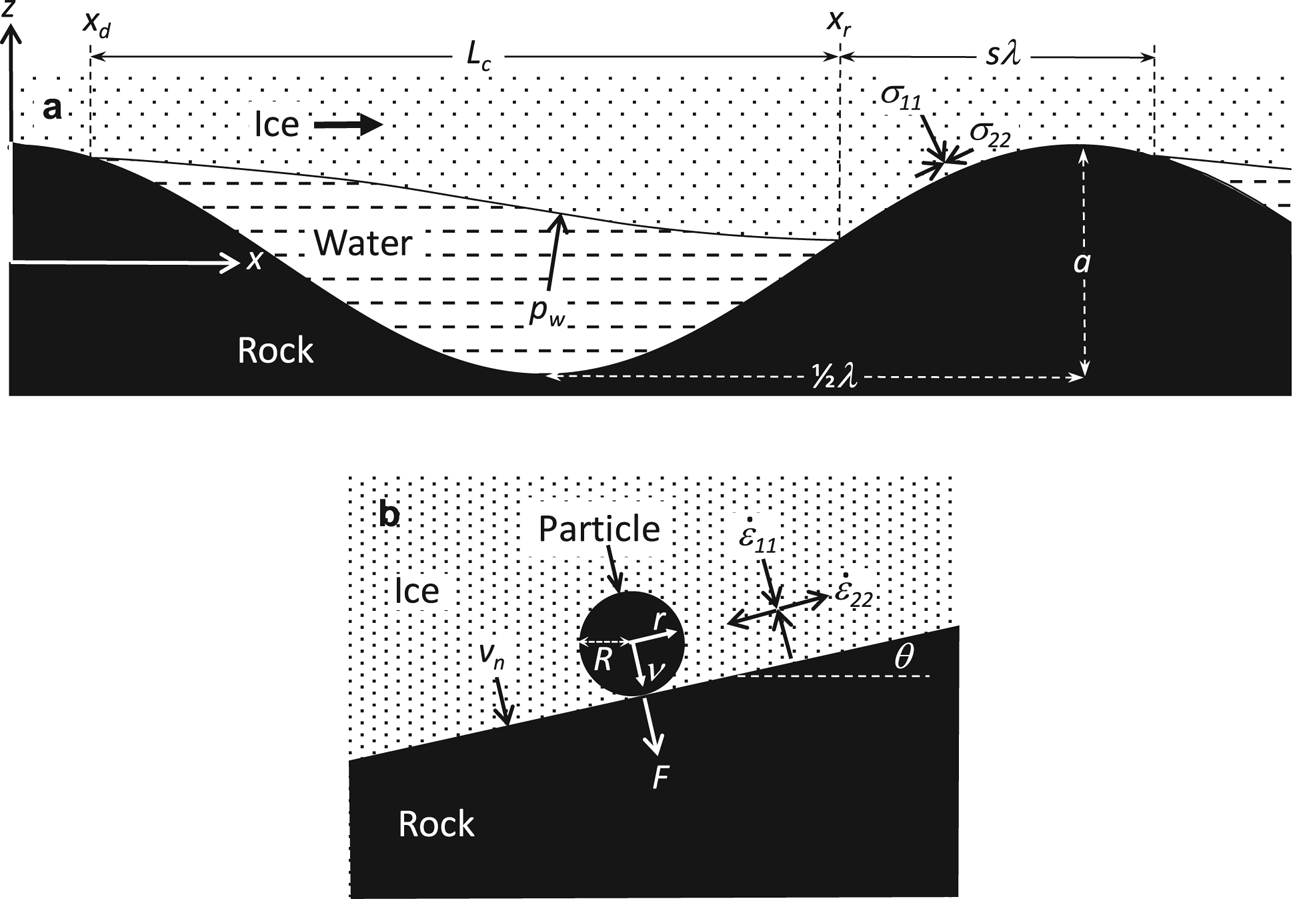
Fig. 1. (a) Model parameters and coordinates for the wavy bed of Lliboutry (Reference Lliboutry1968). (b) Model parameters and coordinates for a particle in frictional contact with the bed over the zone of ice–bed contact, sλ, in panel (a).
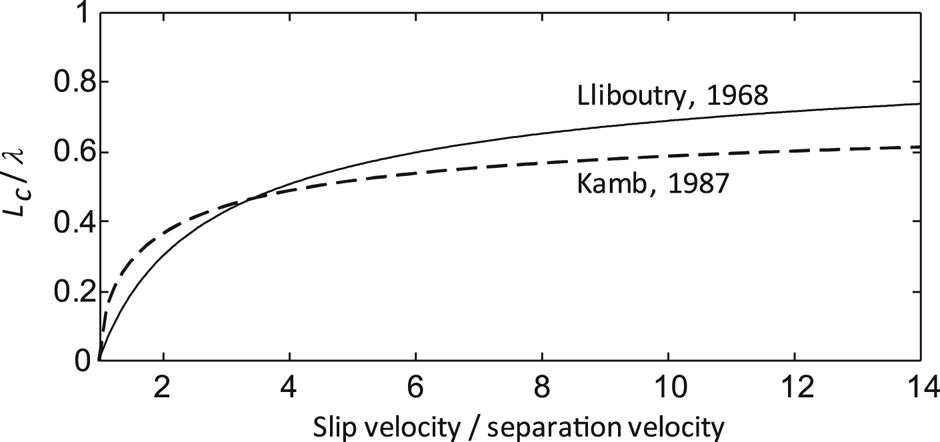
Fig. 2. Cavity length, L c, scaled by the bed wavelength, λ, as a function of slip velocity scaled by the velocity at which ice separates from lee surfaces, as indicated by the theories of Lliboutry (Reference Lliboutry1968) and Kamb (Reference Kamb1987, see his Eqns (8) and (13)).
The flow law of ice is represented by the pre-factor, A, and the creep exponent n (Cuffey and Paterson, Reference Cuffey and Paterson2010, p. 55). Effective pressure N = ρgH cos α − p w, where ρ is the ice density, g is the gravitational acceleration, H is the ice thickness, α is the glacier surface slope and p w is the cavity water pressure. Neglected in deriving Eqn (3) is heat dissipated by water flowing through cavities and resultant melting of cavity roofs; such dissipation is thought to be small in cavities (Walder, Reference Walder1986). Confidence in this estimate of cavity size comes from Kamb (Reference Kamb1987), who considered the same bed geometry and ice rheology and arrived at a similar estimate using a different analysis (Fig. 2).
Also required for estimating basal shear stress is the location, x d, where the ice detaches from the bed:

(Lliboutry, Reference Lliboutry1968), where x d = 0 would correspond to ice detachment at the bump crest (Fig. 1a). For increasing sliding speeds, the point of detachment is increasingly close to the bump crest upstream, and the reattachment point, x r = x d + L c (Fig. 1a) approaches the downstream crest (Fig. 3). These results are qualitatively similar to those of Fowler (Reference Fowler1986) who considered a linear ice rheology, although in his analysis x d extends slightly up-glacier beyond the bump crest, and the ice reattachment point extends farther down-glacier for a given slip velocity scaled by N and ${\rm {\cal R}}$ .
.
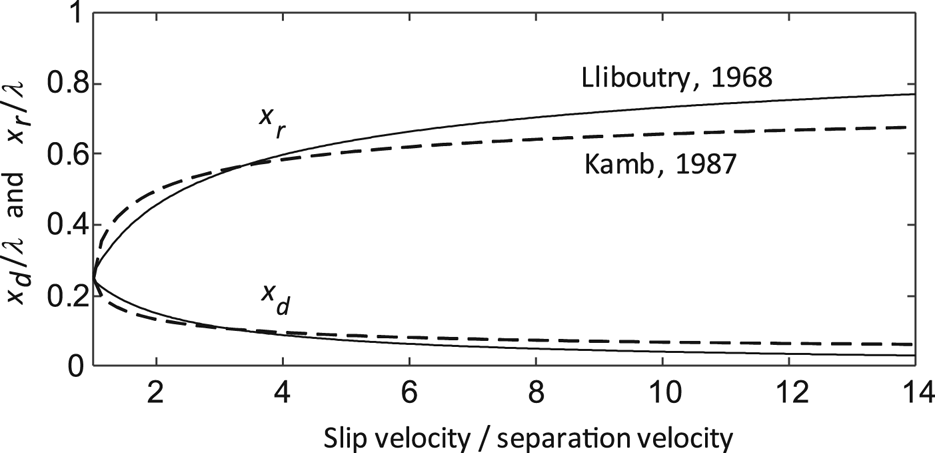
Fig. 3. Points of detachment, x d, and reattachment, x r, of ice, as a function of slip velocity scaled by the velocity at which ice separates from lee surfaces, indicated by the theories of Lliboutry (Reference Lliboutry1968) and Kamb (Reference Kamb1987). Bump crests are at x/λ = 0 and x/λ = 1.0.
The basal drag depends on the normal stress, σ n, that ice exerts on the bed over zones of ice–bed contact. Lliboutry (Reference Lliboutry1968) assumed that this stress varies symmetrically about the centers of such zones where the stress reaches a maximum, to arrive at
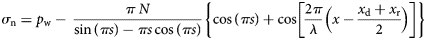
(see his Eqns (10 and 12)). From this stress distribution, he estimated the basal shear stress, τ, for clean ice:
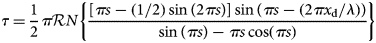
(Lliboutry, Reference Lliboutry1968, his Eqns (13 and 14)), where s depends on sliding speed through Eqn (3). The resultant rate-weakening drag (Fig. 4) is qualitatively similar to that determined in subsequent analyses (Fowler, Reference Fowler1986; Schoof, Reference Schoof2005; Gagliardini and others, Reference Gagliardini, Cohen, Råback and Zwinger2007). A drawback of Lliboutry's model is that he derived separate relationships for sliding velocities below and above the velocity value at which ice–bed separation occurs, resulting in a non-smooth first derivative of the stress relationship at the separation velocity. Thus, Figures 2–4, with sliding velocity scaled by the separation velocity, do not include values <1.0. This scaling is acceptable because we are concerned with the effect of debris on rate-weakening drag that accompanies cavity growth. The separation velocity can be found from Eqn (3) by setting s = 1.
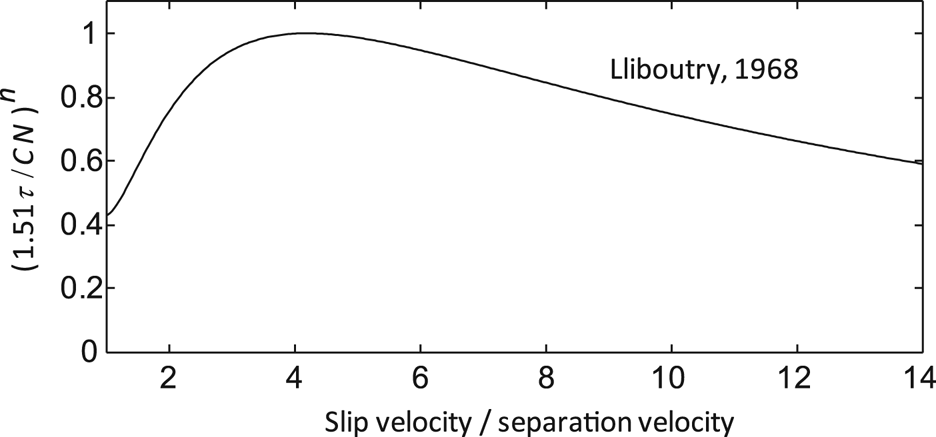
Fig. 4. Sliding rule of Lliboutry (Reference Lliboutry1968) for sliding velocities above those required for ice–bed separation. Shear stress, τ, is scaled following Gagliardini and others (Reference Gagliardini, Cohen, Råback and Zwinger2007) where $C = \pi {\rm {\cal R}\;}$ is the maximum slope of the bed. The factor, 1.51, adjusts τ to bring it into accord with Iken's (Reference Iken1981) bound. Solving for τ in each of her Eqns (3) and (4) and dividing the results yields this factor; it reflects different assumptions made by Lliboutry (Reference Lliboutry1968) and Iken (Reference Iken1981) regarding the distribution of normal stress on zones of ice–bed contact.
is the maximum slope of the bed. The factor, 1.51, adjusts τ to bring it into accord with Iken's (Reference Iken1981) bound. Solving for τ in each of her Eqns (3) and (4) and dividing the results yields this factor; it reflects different assumptions made by Lliboutry (Reference Lliboutry1968) and Iken (Reference Iken1981) regarding the distribution of normal stress on zones of ice–bed contact.
3. Debris-bed friction
Lliboutry's (Reference Lliboutry1968) sliding model allows estimation of rates of ice–bed convergence with stoss surfaces and cavity size as functions of slip velocity. The former controls contact forces between particles and the bed, whereas the latter controls the area of the bed over which debris-bed friction occurs. We wish to explore how the tradeoff between these two variables for different cavity sizes affects the form of the relationship between shear stress and slip velocity.
A major component of ice–bed convergence on stoss surfaces is from extension of ice parallel to the bed as ice flows past bumps (Hallet, Reference Hallet1981). Sliding theory for a sinusoidal bed, in the absence of ice–bed separation and neglecting regelation, yields a component of ice velocity toward the bed everywhere on stoss surfaces at rates that peak at the point midway up stoss surfaces (Nye, Reference Nye1969, see his Eqn (32) in the limit of zero regelation past bumps). Iken's (Reference Iken1981, her Fig. 6a) numerical calculations of the velocity field in Newtonian ice near a sinusoidal bed for the case of steady cavities similarly demonstrate that a streamline near stoss surfaces converges with the bed and that ice speeds up as it moves down-glacier along zones of ice–bed contact, indicative of bed-parallel extension on stoss surfaces. These facts are also confirmed by recent finite-element simulations of the same process with a Glen-type ice rheology (Helanow and others, Reference Helanow, Iverson and Zoet2018). The ubiquity of striations on stoss surfaces (e.g. Hallet, Reference Hallet1979) of large bumps where leeward cavities have been mapped (e.g. Hallet and Anderson, Reference Hallet and Anderson1980) provides further confirmation that extension of ice parallel to the bed during flow past bumps presses debris particles against stoss surfaces – a process that was first recognized by Gilbert (Reference Gilbert1906).
This ice extension causes a component of ice velocity toward the bed that is zero at the bed surface but increases away from the bed in the zone of extension. To estimate the bed-normal ice velocity that results from this ice deformation, v d, we consider the more compressive principal stress, σ 11, to be normal to areas of ice–bed contact, following Lliboutry (Reference Lliboutry1968), so σ 11 = σ n (Fig. 1a). A reasonable choice for the less compressive principal stress is σ 22 = p w, the water pressure in cavities, which confines the ice on each side of the zone of ice–bed contact (Fig. 1a). Making these assumptions, defining the mean stress as p m = 1/2(σ 11 + σ 22), and using Glen's flow law yields the effective strain rate, $\dot{\varepsilon} _{\rm e}$ :
:

where the term in the outermost brackets is the effective shear stress, (1/2σ ijσ ij)1/2 (e.g. Hooke, Reference Hooke2005), and $\overline {\sigma _{\rm n}} \;$ is the normal stress (Eqn (5)) averaged over the zone of ice–bed contact. We idealize this strain rate as uniform in the thin zone of ice adjacent to stoss surfaces where debris particles in contact with the bed reside. Noting that $\dot{\varepsilon} _{\rm e} = (1/\sqrt 2 )\lpar {\dot{\epsilon}_{11}^2 + \; \dot{\epsilon}_{22}^2} \rpar ^{1/2}$
is the normal stress (Eqn (5)) averaged over the zone of ice–bed contact. We idealize this strain rate as uniform in the thin zone of ice adjacent to stoss surfaces where debris particles in contact with the bed reside. Noting that $\dot{\varepsilon} _{\rm e} = (1/\sqrt 2 )\lpar {\dot{\epsilon}_{11}^2 + \; \dot{\epsilon}_{22}^2} \rpar ^{1/2}$ and that for the plane strain of this problem, continuity requires $\dot{\varepsilon} _{11} = -\dot{\varepsilon} _{22}\;$
and that for the plane strain of this problem, continuity requires $\dot{\varepsilon} _{11} = -\dot{\varepsilon} _{22}\;$ (Fig. 1b), then $\dot{\varepsilon} _{\rm e} = \dot{\varepsilon} _{11}$
(Fig. 1b), then $\dot{\varepsilon} _{\rm e} = \dot{\varepsilon} _{11}$ . Integrating $\dot{\varepsilon} _{11}$
. Integrating $\dot{\varepsilon} _{11}$ from the bed surface along a coordinate, ν, normal to the bed indicates that v d = $\dot{\varepsilon} _{11}$
from the bed surface along a coordinate, ν, normal to the bed indicates that v d = $\dot{\varepsilon} _{11}$ ν. The value of v d that is most relevant to particle–bed contact forces is the velocity at the midpoint of a particle (Hallet, Reference Hallet1981), which corresponds to its radius, R (Fig. 1b). Thus, taking ν = R, and using Eqn (7) yields the component of ice velocity toward the bed due to the bed-parallel extension of ice:
ν. The value of v d that is most relevant to particle–bed contact forces is the velocity at the midpoint of a particle (Hallet, Reference Hallet1981), which corresponds to its radius, R (Fig. 1b). Thus, taking ν = R, and using Eqn (7) yields the component of ice velocity toward the bed due to the bed-parallel extension of ice:

The other component of bed-normal ice velocity results from basal melting. The heat flux dissipated by sliding ice is q s = τu. We assume that all of this heat flux and the geothermal heat flux, q G, melt ice only along the ice–bed contacts where ice is coldest, so the rate of basal melting, v m, depends on cavity size through s:

As in the derivation of Eqn (3), heat dissipated by water flowing through cavities is neglected. Equations (8) and (9) provide the total bed-normal ice velocity, v n (Fig. 1b) in zones of ice–bed contact: v n = v d + v m.
Contact force, F, exerted normal to the bed by particles in zones of ice–bed contact, depends on v n because as ice moves toward the bed it exerts a bed-normal drag on particles (Fig. 1b). Watts (Reference Watts1974) determined the drag on an isolated sphere exerted by temperate ice moving by regelation and enhanced creep. Hallet (Reference Hallet1979, Reference Hallet1981) adapted this result and added to it the sphere's buoyant weight in ice to obtain

where η e is the effective viscosity of ice, R * is the controlling particle size, f is an empirical factor >1.0 that accounts for the accentuating effect of the bed proximity on drag, ρ r is the particle density and θ is the angle between the local bed slope and horizontal (Fig. 1b). Particle buoyant weight, as indicated by the right-hand term, is a significant fraction of F only for R > 0.1 m (Hallet, Reference Hallet1979). Experiments with inclusions in ice in which v n has been measured indicate that drag indeed depends on v n (Iverson, Reference Iverson1990; Byers and others, Reference Byers, Cohen and Iverson2012), with f ≈ 2.0 (Byers and others, Reference Byers, Cohen and Iverson2012). Cavities that form in these spaces between particles and the bed led Boulton (Reference Boulton and Coates1974) to suggest that the difference between the ice pressure and water pressure in these cavities controlled contact forces. However, water pressure in cavities of steady size beneath isolated particles on the bed must be at least slightly higher than the mean ice pressure to enable drainage from cavities through the water film along the bed surface to ‘connected’ parts of the subglacial hydraulic system. We thus use Eqn (10) to estimate contact forces but acknowledge that it is contingent on the assumption that water produced by melting along particle surfaces drains through the water film at the ice–rock interface. Equally important is that Eqn (10) applies only to debris particles that are sufficiently isolated from each other that their flow fields do not interact.
Owing to the power-law rheology of ice, η e and R * in Eqn (10) depend on v n. The effective viscosity depends on the flow-law parameters:

where r is the distance from particle centers parallel to the local bed slope and remembering that ν is the coordinate perpendicular to the local bed slope (Fig. 1b). Approximating η e therefore requires choosing a reference value of the shear strain rate, $\dot{\varepsilon} _{r\nu}$ . Neglecting bed-normal gradients in velocity parallel to the local bed slope, $\dot{\varepsilon} _{r\nu} = (1/2)(\; \delta v_{\rm n}/\delta r)$
. Neglecting bed-normal gradients in velocity parallel to the local bed slope, $\dot{\varepsilon} _{r\nu} = (1/2)(\; \delta v_{\rm n}/\delta r)$ . The radial variation in bed-normal velocity, δv n, is at most v n. Taking δv n = v n, and choosing δr as the particle diameter, 2R, then yields
. The radial variation in bed-normal velocity, δv n, is at most v n. Taking δv n = v n, and choosing δr as the particle diameter, 2R, then yields

The resultant value of effective viscosity from Eqn (11) determines in Eqn (10) the value of R *:

where C m is the melting point depression with pressure, and K is a bulk thermal conductivity of particles and ice (Watts, Reference Watts1974).
From the contact force, F, and fractional area of ice–bed contact, s, the component of bed shear stress due to debris-bed friction, τ d, is
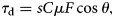
where C is the concentration of particles in contact with the bed (particle number per unit area), μ is the coefficient friction between rock particles and the bed and cos θ isolates the component of stress parallel to the average bed slope, assumed to be zero. Eqn (14) may overestimate τ d because particles may rotate in ice under a torque smaller than the torque, μFR, caused by full mobilization of clast-bed friction. We neglect this complication to maximize the possible effect of debris-bed friction on the sliding rule. For the same reason we consider only maximum values of C, limited by the requirement that debris particles be widely enough spaced so that flow fields around them do not interact. Velocity distributions in ice during its power-law flow past an isolated sphere (Lliboutry and Ritz, Reference Lliboutry and Ritz1978) indicate that particles separated by at least ~1.5 particle diameters satisfy this criterion. This spacing of particles at the bed surface implies that the number of particles per unit area of the bed is

If the same particle spacing applies normal to the bed, then the associated concentration of debris in ice by mass is ~15%.
Equations (3–5) and (8–13) allow estimation of contact forces and areas of ice–bed contact as a function of sliding speed, and Eqn (14) provides the resulting estimate of debris-bed friction, maximized for each particle size through Eqn (15). Table 1 shows relevant parameter values.
Table 1. Parameter values

a Values from Cuffey and Paterson (Reference Cuffey and Paterson2010) unless noted otherwise here or in the text.
b Watts (Reference Watts1974).
c Jaeger and Cook (Reference Jaeger and Cook1979).
d Pollack and others (Reference Pollack, Hurter and Johnson1993).
4. Results
The bed-normal component of ice velocity, v n, in zones of ice–bed contact – the driver for particle–bed contact forces – increases with increasing velocity and cavity size but at a decreasing rate for various particle sizes (Fig. 5a). The normal stress on the bed (Eqn (5)) and the associated rate of ice extension on stoss surfaces are largely responsible for this variation, which reflects cavity growth rate decreasing with increasing slip velocity (Fig. 2). Large particles extend higher in the ice and thus are subjected to larger values of ice–bed convergence from ice extension than smaller particles (Fig. 5a). Contact forces (Eqn (10)) increase similarly with slip velocity (Fig. 5b), but contact forces vary orders-of-magnitude more with particle size than do bed-normal ice velocities. This large variation reflects little drag on small particles due to the efficiency of regelation and much larger drags on larger particles closer to the controlling particle size (R * = 0.03–0.15 m, depending on v n and R, Eqns (11–13)). The effect of a given particle size on debris-bed friction also depends, however, on the particle concentration in ice, which is larger for smaller particles (Eqn (15)). Considering the product, CF, of the particle concentration and contact force indicates that larger particles, nevertheless, have a significantly larger effect on total contact forces than smaller particles (Fig. 6a).
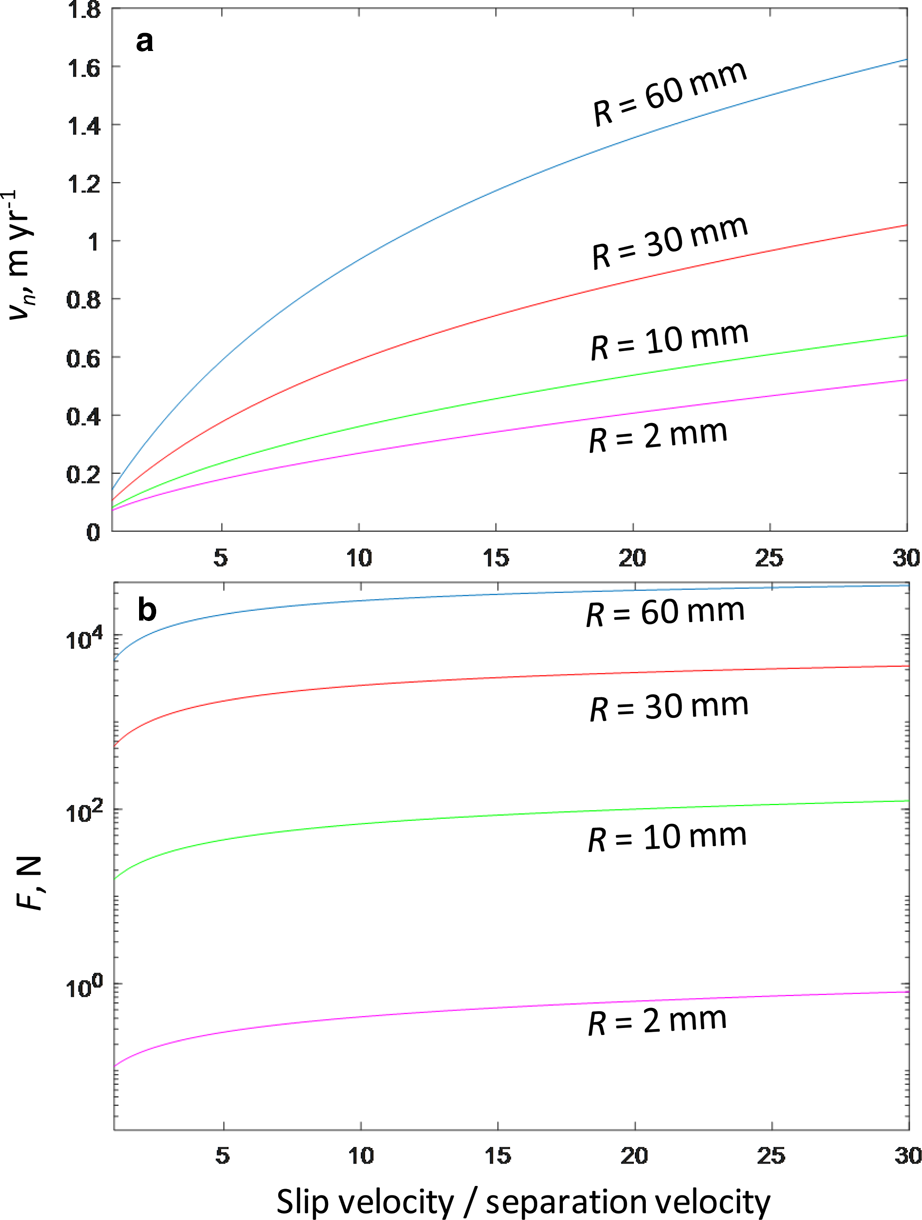
Fig. 5. (a) Convergence velocity, v n, and (b) contact force, F, for different particle radii, R. Bed roughness, ${\rm {\cal R}}$ = 0.1 and effective pressure, N = 500 kPa. This value of N, for the case of basal water pressure at 80% of the ice overburden pressure, corresponds to a glacier ~280 m thick.
= 0.1 and effective pressure, N = 500 kPa. This value of N, for the case of basal water pressure at 80% of the ice overburden pressure, corresponds to a glacier ~280 m thick.
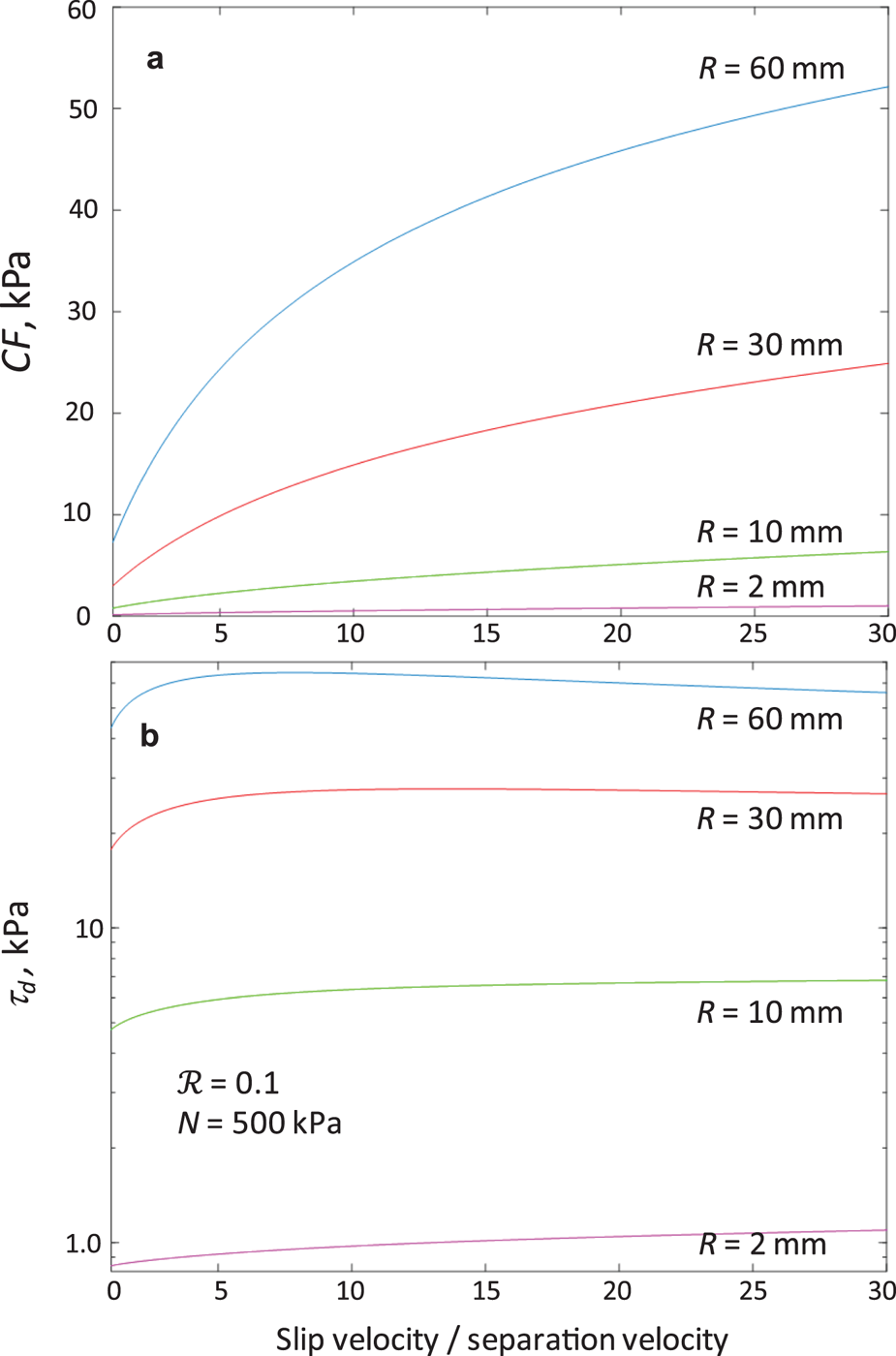
Fig. 6. (a) The product of contact force, F, and debris concentration, C (in particles per m2), and (b) the shear stress caused by debris-bed friction, for different particle radii, R. Bed roughness, ${\rm {\cal R}}$ = 0.1, and effective pressure, N = 500 kPa.
= 0.1, and effective pressure, N = 500 kPa.
Debris-bed friction, therefore, increases with increasing particle size (Fig. 6b). Regardless of particle size, the sensitivity of debris-bed friction to slip velocity is small, owing to growth of cavities with increasing slip velocity, as factored into Eqn (14) through the fractional area of ice–bed contact, s. Interestingly, debris-bed friction does not monotonically increase with slip velocity for all particle sizes. For the two largest particle sizes considered, at a sufficiently high slip velocity debris-bed friction reaches a maximum and declines at still higher slip velocities. This behavior reflects the rapid decrease in the rate at which CF increases with slip velocity for larger particles (Fig. 6a), causing high sensitivity of debris-bed friction to changing cavity size that reverses the slope of the relationship for larger particles.
However, apart from increasing the magnitude of the basal shear stress, the overall effect of debris-bed friction on the form of the sliding rule is small (Fig. 7). Debris-bed friction steepens the ascending limb of the sliding rule and slightly increases the threshold slip velocity at which the peak shear stress occurs, thus reducing the propensity for rate-weakening drag. These effects are minor, however, because decreases in ice–bed contact area with cavity growth mute or reverse the effect of increases in debris-bed friction from increased contact forces. Note that in Figure 7 drag depends on chosen values of bed roughness (0.1) and effective pressure (500 kPa). Although the shear stress scaling for clean ice is independent of these variables (Fig. 4), in Figure 7 we do not use this scaling because it is inappropriate when shear stress depends, in part, on debris friction.
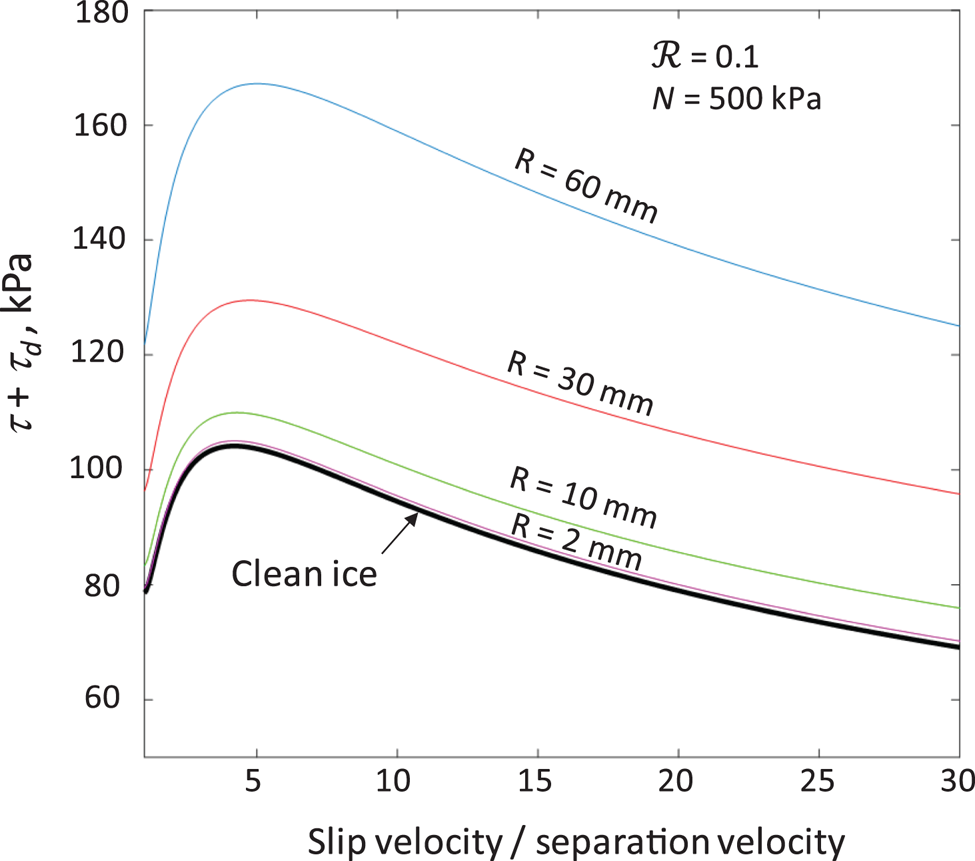
Fig. 7. Sum of shear stress with clean ice, τ, and with debris-bed friction, τ d, for different particle radii, R. Bed roughness, ${\rm {\cal R}}$ = 0.1 and effective pressure, N = 500 kPa.
= 0.1 and effective pressure, N = 500 kPa.
Dependencies of the friction-influenced sliding rule on bed roughness and effective pressure, shown in plots in which both shear stress and slip velocity are unscaled (Figs 8 and 9), further illustrate the importance of cavity size. Smaller bed roughness (Fig. 8), in addition to decreasing the peak stress and the magnitude and velocity range of rate-weakening drag, increases the component of stress due to debris-bed friction. This reflects smaller cavities and larger areas of the bed of over which debris-bed friction acts if roughness is low. For the same reason, debris-bed friction increases with increasing effective pressure (Fig. 9), which reduces cavity size. For small but reasonable values of effective pressure (e.g. 300 kPa), threshold slip velocities for ice–bed separation can be extremely low, and rate-weakening drag can occur over nearly the full range of possible slip velocity. Debris-bed friction does little to alter this effect (Fig. 9).
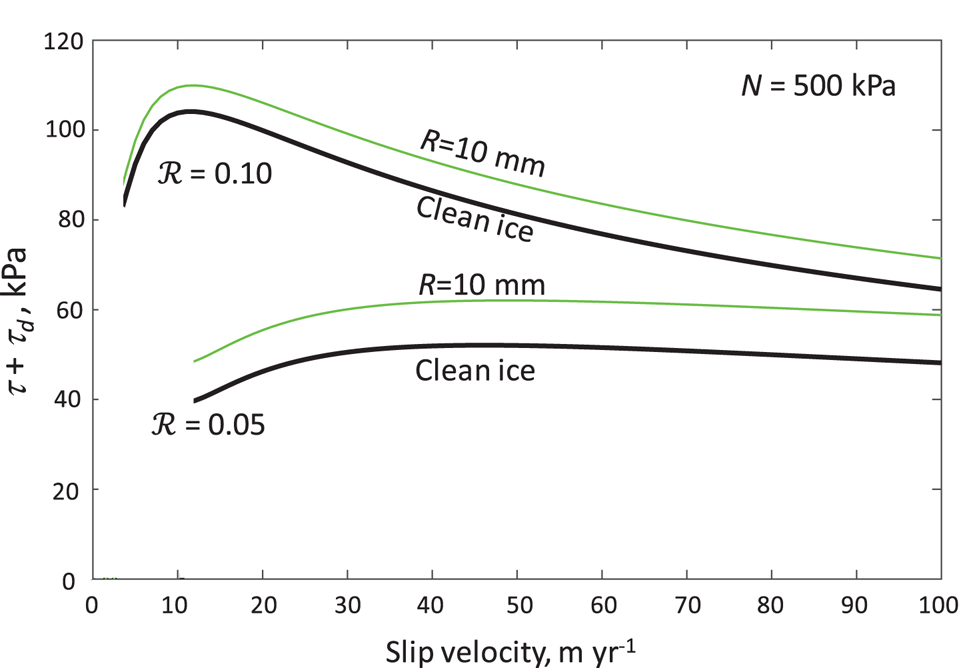
Fig. 8. Sum of shear stress with clean ice, τ, and shear stress from debris-bed friction, τ d, for two values of bed roughness, ${\rm {\cal R}}$ . Particle radius, R = 10 mm, and effective pressure N = 500 kPa.
. Particle radius, R = 10 mm, and effective pressure N = 500 kPa.
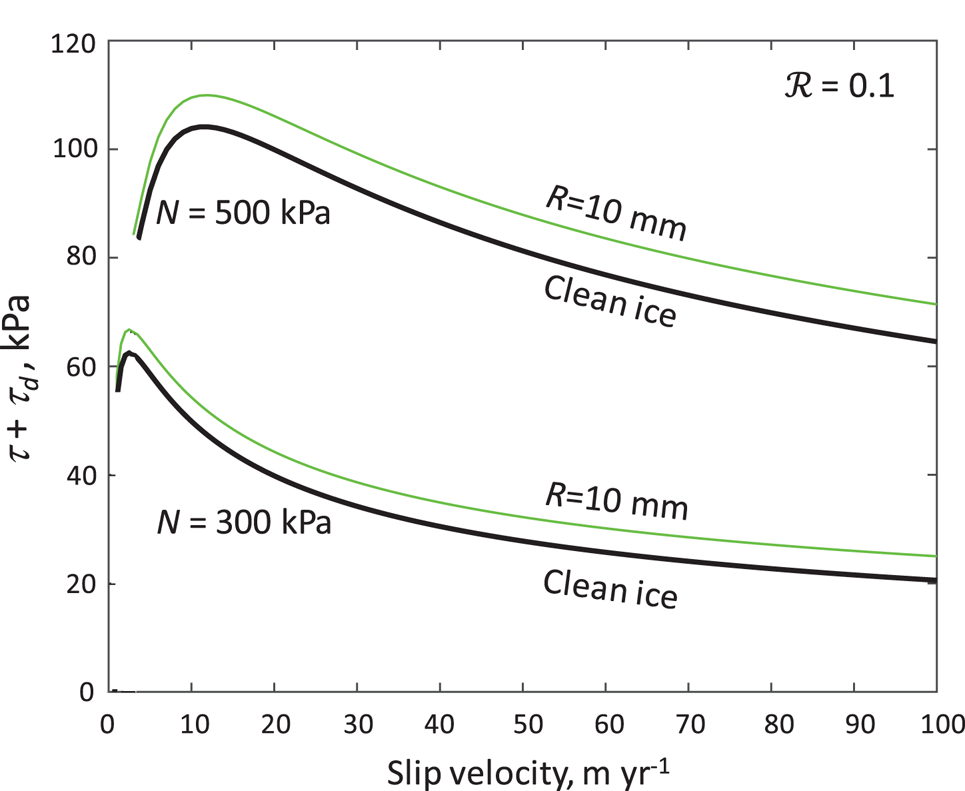
Fig. 9. Sum of shear stress with clean ice, τ, and shear stress from debris-bed friction, τ d, for two values of effective pressure, N. Particle radius, R = 10 mm, and bed roughness, ${\rm {\cal R}}$ = 0.1.
= 0.1.
5. Discussion and conclusions
Increasing cavity size with increasing slip velocity has two opposing effects on debris-bed friction. Larger cavities increase normal stresses on zones of ice–bed contact, with associated higher rates of ice-convergence and contact forces. Larger cavities also, however, reduce the area over which debris-bed friction acts. For all particle sizes, the combination of these effects at low slip velocities causes debris-bed friction to increase with increasing velocity. For sufficiently large particles, debris-bed friction peaks, with rate-weakening friction at higher velocities (Fig. 6). The effect of debris-bed friction on basal shear stress is to steepen the rising limb of the sliding rule and shift the peak in drag to a slightly larger slip velocity (Fig. 7). However, the overall sensitivity of debris-bed friction to sliding speed is sufficiently small that these effects on the form of the sliding rule are minor.
In principle, debris can substantially increase the peak stress (Fig. 7), but accurately estimating this stress has not been our goal. We have maximized debris concentrations without specifying reasonable ranges of particle size. For example, a collection of grapefruit-sized clasts (R = 60 mm, Figs 5–7) with 3R spacing (Eqn (15)) at the bed is unlike any grain-size distribution observed in the basal ice of a glacier. Rather, our goal has been to ask, with debris-bed friction maximized, whether it can have a significant effect on the form of the sliding rule. The answer, within the limitations of the analysis, is no, and that answer should also apply to realistic grain-size distributions in which large particles are few relative to small particles.
Limitations of the analysis include neglecting the effect of debris friction on sliding speed and cavity size and neglecting debris concentrations in ice sufficiently large so that ice flow fields around particles interact. The former is neglected because no analytical model of sliding with ice–bed separation exists for the case of a non-zero shear traction applied at the bed surface, although Morland (Reference Morland1976) considered this problem. Including this effect might influence the tradeoff between contact forces and cavity size with sliding speed. Dense concentrations of debris particles in ice are not common but sometimes observed. A speculation, based on one set of laboratory experiments with dense debris in temperate ice (Iverson, Reference Iverson1993), is that micro-cavities beneath adjacent particles merge so that an irregular water layer, much thicker than the normal water film, exists at the bed surface. If this layer were hydraulically transmissive enough for water pressure within it to be controlled by the pressure in the subglacial hydraulic system, effective pressure could become the dominant control variable for contact forces. In this case, particle–bed contact forces could be much higher than for the case of sparse debris.
These results indicate that debris-bed friction does not eliminate or significantly lessen rate-weakening drag indicated by idealized theories and experiments, leaving open the major question of how actual hard beds may suppress rate weakening. One possibility is that some bumps on glacier beds may be both large enough to remain unsubmerged in cavities and have stoss faces that are steeper than those already submerged (Schoof, Reference Schoof2005). Alternatively, on actual glacier beds bump crests may align too poorly along a flowline for cavities to submerge stoss surfaces sufficiently under the operative range of sliding speed (Zoet and Iverson, Reference Zoet and Iverson2016). Also, the degree of convexity of stoss surfaces in contact with ice could be important. Development of sliding theory for realistic, 3-D bedrock surfaces, therefore, might allow the physics of hard-bedded sliding to be reconciled with large-scale glacier flow models that neglect rate-weakening drag.
Alternatively, such theory might show that rate-weakening drag on actual hard beds is not suppressed and so point to a major inadequacy in how the basal boundary condition in glacier flow models is handled. As discussed previously (Lliboutry, Reference Lliboutry1968; Fowler, Reference Fowler1987; Schoof, Reference Schoof2005), a glacier with a bed that effectively becomes slipperier with increasing slip velocity would be inherently prone to fast flow and associated mass losses.
Acknowledgements
This work was supported by a grant to NRI and LKZ from the US National Science Foundation (EAR-1660972). We thank reviewers, J.S. Walder and T. Creyts, and scientific editor, M. Truffer, for helpful comments.


















