Hostname: page-component-84b7d79bbc-g5fl4 Total loading time: 0 Render date: 2024-07-27T22:44:59.477Z Has data issue: false hasContentIssue false
  • English
  • Français

A thermal energy storage process with controlled input

Published online by Cambridge University Press:  01 July 2016

D. J. Daley  and
J. Haslett
D. J. Daley*
Affiliation:
The Australian National University
J. Haslett*
Affiliation:
Trinity College, Dublin
*
∗Postal address: Statistics Department (IAS), The Australian National University, P.O. Box 4, Canberra, ACT 2600, Australia.
∗∗Postal address: Statistics Department, Trinity College, Dublin, Ireland.
Get access Rights & Permissions [Opens in a new window]

Abstract

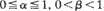The stochastic process {Xn} satisfying Xn+1 = max{Yn+1+ αβ Xn, βXn} where {Yn} is a stationary sequence of non-negative random variables and , 0<β <1, can be regarded as a simple thermal energy storage model with controlled input. Attention is mostly confined to the study of μ = EX where the random variable X has the stationary distribution for {Xn}. Even for special cases such as i.i.d. Yn or α = 0, little explicit information appears to be available on the distribution of X or μ . Accordingly, bounding techniques that have been exploited in queueing theory are used to study μ . The various bounds are illustrated numerically in a range of special cases.

Keywords

CONTROLLED INPUT STORAGE MODELAUTOREGRESSIVE MODELQUEUEING INEQUALITIESCOMPARISON TECHNIQUES
Type
Research Article
Information
Advances in Applied Probability , Volume 14 , Issue 2 , June 1982 , pp. 257 - 271
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research carried out while this author was visiting CSIRO Division of Mathematics and Statistics, Canberra.

References

Andrews, G. E. (1976) The Theory of Partitions. Addison-Wesley, Reading, MA.Google Scholar
Daley, D. J. (1968) Stochastically monotone Markov chains. Z. Wahrscheinlichkeitsth. 10, 305–317.Google Scholar
Daley, D. J. (1977) Inequalities for moments of tails of random variables, with a queueing application. Z. Wahrscheinlichkeitsth. 41, 139–143.Google Scholar
Daley, D. J. (1981) The absolute convergence of weighted sums of stationary sequences of random variables. Z. Wahrscheinlichkeitsth. 58, 199–203.Google Scholar
Haslett, J. (1979) Problems in the stochastic storage of solar thermal energy. In Analysis and Optimization of Stochastic Systems, ed. Jacobs, O. Academic Press, London.Google Scholar
Hellend, I. S. and Nilsen, T. S. (1976) On a general random exchange model. J. Appl. Prob. 13, 781–790.Google Scholar
Kawata, T. (1972) Fourier Analyis in Probability Theory. Academic Press, New York.Google Scholar
Kingman, J. F. C. (1962) Some inequalities for the queue GI/G/1. Biometrika 49, 315–324.CrossRefGoogle Scholar
Marshall, K. T. (1968) Some inequalities in queueing. Operat. Res. 16, 651–665.Google Scholar
Stoyan, D. (1977) Qualitative Eigenschaften Abschätzungen stochastischer Modelle. Akademie-Verlag, Berlin. (Revised edition in English: Comparison Methods for Queues and Other Stochastic Models. Wiley, Chichester.) Google Scholar
Trengove, C. D. (1978) Bounds for the Mean Waiting Time in Queues. , University of Melbourne.Google Scholar
Tweedie, R. L. (1976) Criteria for classifying general Markov chains. Adv. Appl. Prob. 8, 737–771.Google Scholar