Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Asmussen, Søren
1978.
On the law of the iterated logarithm and central limit theorem for branching processes.
Advances in Applied Probability,
Vol. 10,
Issue. 2,
p.
305.
Asmussen, Søren
1982.
On The Role of a Certain Eigenvalue in Estimating the Growth Rate of a Branching Process.
Australian Journal of Statistics,
Vol. 24,
Issue. 2,
p.
151.
Nanthi, K.
1982.
Estimation of the variance for the multitype Galton–Watson process.
Journal of Applied Probability,
Vol. 19,
Issue. 2,
p.
408.
Nanthi, K.
1982.
Estimation of the variance for the multitype Galton–Watson process.
Journal of Applied Probability,
Vol. 19,
Issue. 02,
p.
408.
Heyde, C. C.
1986.
On the use of time series representations of population models.
Journal of Applied Probability,
Vol. 23,
Issue. A,
p.
345.
Asmussen, Søren
1986.
Semi-Markov Models.
p.
385.
Jarušková, Daniela
1986.
Fibonacci Numbers and Their Applications.
p.
99.
Heyde, C. C.
1986.
On the use of time series representations of population models.
Journal of Applied Probability,
Vol. 23,
Issue. A,
p.
345.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Badalbaev, I. S.
and
Mukhitdinov, A.
1991.
On the Limit Distributions of Some Functionals in Multi-Type Branching Processes.
Theory of Probability & Its Applications,
Vol. 35,
Issue. 4,
p.
625.
Lee, Chinsan
and
Yang, Grace L.
1995.
A multitype decomposable age-dependent branching process and its applications.
Journal of Applied Probability,
Vol. 32,
Issue. 03,
p.
591.
Carvalho, Maria Lucília
1997.
A joint estimator for the eigenvalues of the reproduction mean matrix of a multitype Galton-Watson process.
Linear Algebra and its Applications,
Vol. 264,
Issue. ,
p.
189.
Chaabane, Faouzi
and
Maaouia, Faïza
2000.
Théorèmes limites avec poids pour les martingales vectorielles.
ESAIM: Probability and Statistics,
Vol. 4,
Issue. ,
p.
137.
Athreya, K.B.
and
Vidyashankar, A.N.
2001.
Stochastic Processes: Theory and Methods.
Vol. 19,
Issue. ,
p.
35.
Chi, Zhiyi
2004.
Limit laws of estimators for critical multi-type Galton–Watson processes.
The Annals of Applied Probability,
Vol. 14,
Issue. 4,
Maaouia, F.
and
Touati, A.
2005.
Identification of multitype branching processes.
The Annals of Statistics,
Vol. 33,
Issue. 6,
González, Miguel
Mota, Manuel
and
Ramos, Alfonso
2007.
MOMENT ESTIMATION IN THE CLASS OF BISEXUAL BRANCHING PROCESSES WITH POPULATION–SIZE DEPENDENT MATING.
Australian & New Zealand Journal of Statistics,
Vol. 49,
Issue. 1,
p.
37.
González, M.
Martín, J.
Martínez, R.
and
Mota, M.
2008.
Non-parametric Bayesian estimation for multitype branching processes through simulation-based methods.
Computational Statistics & Data Analysis,
Vol. 52,
Issue. 3,
p.
1281.
Ren, Yan-Xia
Song, Renming
and
Zhang, Rui
2014.
Central Limit Theorems for Super Ornstein-Uhlenbeck Processes.
Acta Applicandae Mathematicae,
Vol. 130,
Issue. 1,
p.
9.
Pénisson, Sophie
2014.
Estimation of the infection parameter of an epidemic modeled by a branching process.
Electronic Journal of Statistics,
Vol. 8,
Issue. 2,
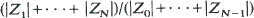 which depends on the total generation sizes
which depends on the total generation sizes 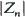 only.
only.

