Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-21T13:08:36.899Z Has data issue: false hasContentIssue false
  • English
  • Français

Information ranking and power laws on trees

Part of: Markov processes Stochastic analysis Limit theorems Special processes

Published online by Cambridge University Press:  01 July 2016

Predrag R. Jelenković  and
Mariana Olvera-Cravioto
Predrag R. Jelenković*
Affiliation:
Columbia University
Mariana Olvera-Cravioto*
Affiliation:
Columbia University
*
∗ Postal address: Department of Electrical Engineering, Columbia University, New York, NY 10027, USA.
∗∗ Postal address: Department of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027, USA. Email address: molvera@ieor.columbia.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the stochastic analysis of information ranking algorithms of large interconnected data sets, e.g. Google's PageRank algorithm for ranking pages on the World Wide Web. The stochastic formulation of the problem results in an equation of the form 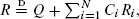where N, Q, {Ri}i≥1, and {C, Ci}i≥1 are independent nonnegative random variables, the {C, Ci}i≥1 are identically distributed, and the {Ri}i≥1 are independent copies of 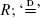stands for equality in distribution. We study the asymptotic properties of the distribution of R that, in the context of PageRank, represents the frequencies of highly ranked pages. The preceding equation is interesting in its own right since it belongs to a more general class of weighted branching processes that have been found to be useful in the analysis of many other algorithms. Our first main result shows that if ENE[Cα] = 1, α > 0, and Q, N satisfy additional moment conditions, then R has a power law distribution of index α. This result is obtained using a new approach based on an extension of Goldie's (1991) implicit renewal theorem. Furthermore, when N is regularly varying of index α > 1, ENE[Cα] < 1, and Q, C have higher moments than α, then the distributions of R and N are tail equivalent. The latter result is derived via a novel sample path large deviation method for recursive random sums. Similarly, we characterize the situation when the distribution of R is determined by the tail of Q. The preceding approaches may be of independent interest, as they can be used for analyzing other functionals on trees. We also briefly discuss the engineering implications of our results.

Keywords

Information rankingstochastic recursionstochastic fixed point equationweighted branching processpower lawregular variationimplicit renewal theorylarge deviation

MSC classification

Primary: 60H25: Random operators and equations
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60F10: Large deviations 60K05: Renewal theory
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 42 , Issue 4 , December 2010 , pp. 1057 - 1093
Copyright
Copyright © Applied Probability Trust 2010 

References

Alsmeyer, G. and Kuhlbusch, D. (2010). Double martingale structure and existence of ϕ-moments for weighted branching processes. To appear in Münster J. Math. Google Scholar
Alsmeyer, G. and Rösler, U. (2006). A stochastic fixed point equation related to weighted branching with deterministic weights. Electron. J. Prob. 11, 27–56.CrossRefGoogle Scholar
Asmussen, S. (1998). Subexponential asymptotics for stochastic processes: extremal behavior, stationary distributions and first passage probabilities. Ann. Appl. Prob. 8, 354–474.Google Scholar
Asmussen, S. (2003). Applied Probability and Queues. Springer, New York.Google Scholar
Athreya, K. B., McDonald, D. and Ney, P. (1978). Limit theorems for semi-Markov processes and renewal theory for Markov chains. Ann. Prob. 6, 788–797.Google Scholar
Athreya, K. B. and Ney, P. E. (2004). Branching Processes. Dover, Mineola, NY.Google Scholar
Baltrūnas, A., Daley, D. J. and Klüppelberg, C. (2004). Tail behavior of the busy period of a GI/GI/1 queue with subexponential service times. Stoch. Process. Appl. 111, 237–258.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987). Regular Variation. Cambridge University Press.Google Scholar
Borovkov, A. (2000). Estimates for the distribution of sums and maxima of sums of random variables without the Cramér condition. Siberian Math J. 41, 811–848.Google Scholar
Brandt, A. (1986). The stochastic equation y n+1 = a n y n + b n with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
Brin, S. and Page, L. (1998). The anatomy of a large-scale hypertextual Web search engine. Comput. Networks ISDN Systems 30, 107–117.Google Scholar
Chow, Y. S. and Teicher, H. (1988). Probability Theory, 2nd edn. Springer, New York.Google Scholar
De Meyer, A. and Teugels, J. L. (1980). On the asymptotic behaviour of the distributions of the busy period and service time in M/G/1. J. Appl. Prob. 17, 802–813.CrossRefGoogle Scholar
Denisov, D., Foss, S. and Korshunov, D. (2009). Asymptotics of randomly stopped sums in the presence of heavy tails. Preprint. Available at the http://arxiv.org/abs/0808.3697v3.Google Scholar
Fill, J. A. and Janson, S. (2001). Approximating the limiting Quicksort distribution. Random Structures Algorithms 19, 376–406.CrossRefGoogle Scholar
Goldie, C. M. (1991). Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.Google Scholar
Gyöngyi, Z., Garcia-Molina, H. and Pedersen, J. (2004). Combating Web spam with TrustRank. Tech. Rep., Stanford University.Google Scholar
Iksanov, A. M. (2004). Elementary fixed points of the BRW smoothing transforms with infinite number of summands. Stoch. Process. Appl. 114, 27–50.Google Scholar
Jelenković, P. R. and Momčilović, P. (2004). Large deviations of square root insensitive random sums. Math. Operat. Res. 29, 398–406.Google Scholar
Jelenković, P. R. and Olvera-Cravioto, M. (2009). Information ranking and power laws on trees. Preprint. Available at http://arxiv.org/abs/0905.1738.Google Scholar
Jelenković, P. R. and Tan, J. (2010). Modulated branching processes, origins of power laws and queueing duality. Math. Operat. Res. 35, 807–829.CrossRefGoogle Scholar
Jessen, A. H. and Mikosch, T. (2006). Regularly varying functions. Publ. Inst. Math. 80, 171–192.Google Scholar
Kesten, H. (1973). Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.Google Scholar
Kleinberg, J. M. (1999). Authoritative sources in a hyperlinked environment. J. ACM 46, 604–632.Google Scholar
Kuhlbusch, D. (2004). On weighted branching processes in random environment. Stoch. Process. Appl. 109, 113–144.Google Scholar
Litvak, N., Scheinhardt, W. R. W. and Volkovich, Y. (2007). In-degree and PageRank: why do they follow similar power laws? Internet Math. 4, 175–198.Google Scholar
Liu, Q. (1998). Fixed points of a generalized smoothing transformation and applications to the branching random walk. Adv. Appl. Prob. 30, 85–112.Google Scholar
Liu, Q. (2000). On generalized multiplicative cascades. Stoch. Process. Appl. 86, 263–286.Google Scholar
Mikosch, T. and Samorodnitsky, G. (2000). The supremum of a negative drift random walk with dependent heavy-tailed steps. Ann. Appl. Prob. 10, 1025–1064.Google Scholar
Nagaev, S. V. (1982). On the asymptotic behavior of one-sided large deviation probabilities. Theory Prob. Appl. 26, 362–366.Google Scholar
Rösler, U. (1993). The weighted branching process. In Dynamics of Complex and Irregular Systems (Bielefeld, 1991), World Science Publishing, River Edge, NJ, pp. 154–165.Google Scholar
Rösler, U. and Rüschendorf, L. (2001). The contraction method for recursive algorithms. Algorithmica 29, 3–33.CrossRefGoogle Scholar
Rösler, U., Topchi, V. A. and Vatutin, V. A. (2000). Convergence conditions for the weighted branching process. Discrete Math. Appl. 10, 5–21.Google Scholar
Volkovich, Y. (2009). Stochastic analysis of Web page ranking. , University of Twente.Google Scholar
Volkovich, Y. and Litvak, N. (2010). Asymptotic analysis for personalized Web search. Adv. Appl. Prob. 42, 577–604.CrossRefGoogle Scholar
Volkovich, Y., Litvak, N. and Donato, D. (2007). Determining factors behind the Pagerank log-log plot. In Algorithms and Models for the Web-Graph, Springer, Berlin, pp. 108–123.Google Scholar
Zwart, A. P. (2001). Tail asymptotics for the busy period in the GI/G/1 queue. Math. Operat. Res. 26, 485–493.Google Scholar