Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T21:25:19.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Empirical clustering of bursts of openings in markov and semi-markov models of single channel gating incorporating time interval omission

Part of: Special processes Markov processes Physiological, cellular and medical topics Basic linear algebra

Published online by Cambridge University Press:  01 July 2016

Frank Ball
Frank Ball*
Affiliation:
University of Nottingham
*
*Postal address: Department of Mathematics, University of Nottingham, University Park, Nottingham NG7 2RD, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

The gating mechanism of a single ion channel is usually modelled by a continuous-time Markov chain with a finite state space, partitioned into two classes termed ‘open’ and ‘closed’. It is possible to observe only which class the process is in. A burst of channel openings is defined to be a succession of open sojourns separated by closed sojourns all having duration less than t0. Let N(t) be the number of bursts commencing in (0, t]. Then 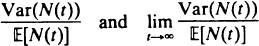are measures of the degree of temporal clustering of bursts. We develop two methods for determining the above measures. The first method uses an embedded Markov renewal process and remains valid when the underlying channel process is semi-Markov and/or brief sojourns in either the open or closed classes of state are undetected. The second method uses a ‘backward’ differential-difference equation.

The observed channel process when brief sojourns are undetected can be modelled by an embedded Markov renewal process, whose kernel is shown, by exploiting connections with bursts when all sojourns are detected, to satisfy a differential-difference equation. This permits a unified derivation of both exact and approximate expressions for the kernel, and leads to a thorough asymptotic analysis of the kernel as the length of undetected sojourns tends to zero.

Keywords

CONTINUOUS-TIME MARKOV CHAINMARKOV RENEWAL PROCESSAGGREGATED PROCESSSINGLE ION CHANNEL MODELLINGFUNDAMENTAL MATRIXSPECTRAL REPRESENTATIONDIFFERENTIAL-DIFFERENCE EQUATIONPERTURBATION THEORY

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 60K15: Markov renewal processes, semi-Markov processes 92C05: Biophysics 15A99: Miscellaneous topics
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 4 , December 1997 , pp. 909 - 946
Copyright
Copyright © Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, F. G. and Davies, S. S. (1997) Clustering of bursts of openings in Markov and semi-Markov models of single channel gating. Adv. Appl. Prob. 29, 92–113.Google Scholar
Ball, F. G., Milne, R. K. and Yeo, G. F. (1991) Aggregated semi-Markov processes incorporating time interval omission. Adv. Appl. Prob. 23, 772–797.CrossRefGoogle Scholar
Ball, F. G., Milne, R. K. and Yeo, G. F. (1993a) On the exact distribution of observed open times in single ion channel models. J. Appl. Prob. 30, 529–537.CrossRefGoogle Scholar
Ball, F. G., Milne, R. K. and Yeo, G. F. (1994) Continuous-time Markov chains in a random environment, with applications to ion channel modelling. Adv. Appl. Prob. 26, 919–946.CrossRefGoogle Scholar
Ball, F. G. and Rice, J. A. (1992) Stochastic models for ion channels: introduction and bibliography. Math. Biosci. 112, 189–206.CrossRefGoogle ScholarPubMed
Ball, F. G. and Sansom, M. S. P. (1987) Temporal clustering of ion channel openings incorporating time interval omission. IMA J. Math. Appl. Medicine Biol. 4, 333–361.Google Scholar
Ball, F. G. and Sansom, M. S. P. (1988) Aggregated Markov processes incorporating time interval omission. Adv. Appl. Prob. 20, 546–572.Google Scholar
Ball, F. G., Yeo, G. F., Milne, R. K., Edeson, R. O., Masden, ?. W. and Sansom, M. S. P. (1993b) Single ion channel models incorporating aggregation and time interval omission. Biophys. J. 64, 357–374.Google Scholar
Bellman, R. (1970) Introduction to Matrix Analysis. 2nd edn. McGraw-Hill, New York.Google Scholar
Bellman, R. and Cooke, K. L. (1963) Differential-Difference Equations. Academic Press, New York.Google Scholar
Činlar, E. (1975) Introduction to Stochastic Processes. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1977) Relaxation and fluctuations of membrane currents that flow through drug-operated channels. Proc. R. Soc. London ? 199, 231–261.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1981) On the stochastic properties of single ion channels. Proc. R. Soc. London ? 211, 205–235.Google ScholarPubMed
Colquhoun, D. and Hawkes, A. G. (1982) On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Phil. Trans. R. Soc. London B 300, 1–59.Google Scholar
Colquhoun, D. and Sakmann, B. (1981) Fluctuations in the microsecond time range of the current through single acetylcholine receptor ion channels. Nature 294, 464–466.Google Scholar
Fredkin, D. R., Montal, M. and Rice, J. A. (1985) Identification of aggregated Markovian models: application to the nicotinic acetylcholine receptor. In Proc. Berkeley Conf. in Honor of Jerzy Neyman and Jack Kiefer, Vol. 1. ed. Le Cam, L. and Olshen, R. Wadworth, Belmont, CA. pp. 269–290.Google Scholar
Goursat, E. (1904) A Course in Mathematical Analysis. Volume I: Derivatives and Differentials , Definite Integrals, Expansion in Series, Applications to Geometry. Ginn, Boston.Google Scholar
Goursat, E. (1916) A Course in Mathematical Analysis. Volume II Part One: Functions of a Complex Variable. Ginn, Boston.Google Scholar
Hawkes, A. G., Jalali, A. and Colquhoun, D. (1990) The distributions of the apparent open times and shut times in a single channel record when brief events cannot be detected. Phil. Trans. R. Soc. London A 332, 511–538.Google Scholar
Hawkes, A. G., Jalali, A. and Colquhoun, D. (1992) Asymptotic distributions of apparent open times and shut times in a single channel record allowing for the omission of brief events. Phil. Trans. R. Soc. London B 337, 383–404.Google Scholar
Hunter, J. J. (1969) On the moments of Markov renewal processes. Adv. Appl. Prob. 1, 188–210.Google Scholar
Jalali, A. (1988) New solutions of an old problem. Privately circulated note.Google Scholar
Jalali, A. (1989) Comments on a paper of Ball and Sansom. Privately circulated note.Google Scholar
Jalali, A. and Hawkes, A. G. (1992a) The distribution of apparent occupancy times in a two-state Markov process in which brief events cannot be detected. Adv. Appl. Prob. 24, 288–301.CrossRefGoogle Scholar
Jalali, A. and Hawkes, A. G. (1992b) Generalised eigenproblems arising in aggregated Markov processes allowing for time interval omission. Adv. Appl. Prob. 24, 302–321.CrossRefGoogle Scholar
Keilson, J. (1979) Markov Chain Models—Rarity and Exponentiality. Springer, New York.Google Scholar
Kelly, F. P. (1979) Reversibility and Stochastic Networks. Wiley, Chichester.Google Scholar
Kemeny, J. and Snell, J. (1976) Finite Markov Chains. 2nd edn. Springer, New York.Google Scholar
Kijima, S. and Kijima, H. (1987) Statistical analysis of channel current from a membrane patch. I. Some stochastic properties of ion channels or molecular systems in equilibrium. J. Theoret. Biol. 128, 423–434.Google Scholar
Lancaster, P. (1969) Theory of Matrices. Academic Press, New York.Google Scholar
Masuda, Y. and Sumita, U. (1987) Analysis of a counting process associated with a semi-Markov process: number of entries into a subset of state space. Adv. Appl. Prob. 19, 767–783.Google Scholar
Morrison, D. F. (1976) Multivariate Statistical Methods. McGraw-Hill, New York.Google Scholar
Pyke, R. (1961) Markov renewal processes: definitions and preliminary properties. Ann. Math. Statist. 32, 1231–1242.Google Scholar
Roux, B. and Sauvé, R. (1985) A general solution to the time interval omission problem applied to single channel analysis. Biophys. J. 48, 149–158.Google Scholar
Sakmann, B. and Neher, E. (1983) Single-Channel Recording. Plenum, New York.Google Scholar
Sakmann, B., Patlak, J. and Neher, E. (1980) Single acetylcholine-activated channels show burst-kinetics in presence of desensitizing concentrations of agonist. Nature 286, 71–73.Google Scholar
Seneta, E. (1973) Non-Negative Matrices. Allen and Unwin, London.Google Scholar