Article contents
Simulation of elliptic and hypo-elliptic conditional diffusions
Published online by Cambridge University Press: 29 April 2020
Abstract
Suppose X is a multidimensional diffusion process. Assume that at time zero the state of X is fully observed, but at time 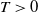 $T>0$
only linear combinations of its components are observed. That is, one only observes the vector
$T>0$
only linear combinations of its components are observed. That is, one only observes the vector 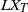 $L X_T$
for a given matrix L. In this paper we show how samples from the conditioned process can be generated. The main contribution of this paper is to prove that guided proposals, introduced in [35], can be used in a unified way for both uniformly elliptic and hypo-elliptic diffusions, even when L is not the identity matrix. This is illustrated by excellent performance in two challenging cases: a partially observed twice-integrated diffusion with multiple wells and the partially observed FitzHugh–Nagumo model.
$L X_T$
for a given matrix L. In this paper we show how samples from the conditioned process can be generated. The main contribution of this paper is to prove that guided proposals, introduced in [35], can be used in a unified way for both uniformly elliptic and hypo-elliptic diffusions, even when L is not the identity matrix. This is illustrated by excellent performance in two challenging cases: a partially observed twice-integrated diffusion with multiple wells and the partially observed FitzHugh–Nagumo model.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 8
- Cited by


