Article contents
Limit theorems for process-level Betti numbers for sparse and critical regimes
Published online by Cambridge University Press: 29 April 2020
Abstract
The objective of this study is to examine the asymptotic behavior of Betti numbers of Čech complexes treated as stochastic processes and formed from random points in the d-dimensional Euclidean space 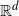 ${\mathbb{R}}^d$
. We consider the case where the points of the Čech complex are generated by a Poisson process with intensity nf for a probability density f. We look at the cases where the behavior of the connectivity radius of the Čech complex causes simplices of dimension greater than
${\mathbb{R}}^d$
. We consider the case where the points of the Čech complex are generated by a Poisson process with intensity nf for a probability density f. We look at the cases where the behavior of the connectivity radius of the Čech complex causes simplices of dimension greater than 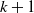 $k+1$
to vanish in probability, the so-called sparse regime, as well when the connectivity radius is of the order of
$k+1$
to vanish in probability, the so-called sparse regime, as well when the connectivity radius is of the order of 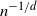 $n^{-1/d}$
, the critical regime. We establish limit theorems in the aforementioned regimes: central limit theorems for the sparse and critical regimes, and a Poisson limit theorem for the sparse regime. When the connectivity radius of the Čech complex is
$n^{-1/d}$
, the critical regime. We establish limit theorems in the aforementioned regimes: central limit theorems for the sparse and critical regimes, and a Poisson limit theorem for the sparse regime. When the connectivity radius of the Čech complex is 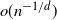 $o(n^{-1/d})$
, i.e. the sparse regime, we can decompose the limiting processes into a time-changed Brownian motion or a time-changed homogeneous Poisson process respectively. In the critical regime, the limiting process is a centered Gaussian process but has a much more complicated representation, because the Čech complex becomes highly connected with many topological holes of any dimension.
$o(n^{-1/d})$
, i.e. the sparse regime, we can decompose the limiting processes into a time-changed Brownian motion or a time-changed homogeneous Poisson process respectively. In the critical regime, the limiting process is a centered Gaussian process but has a much more complicated representation, because the Čech complex becomes highly connected with many topological holes of any dimension.
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 11
- Cited by


